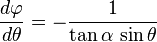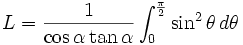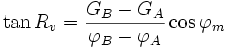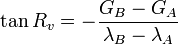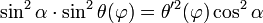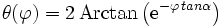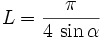Loxodromie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
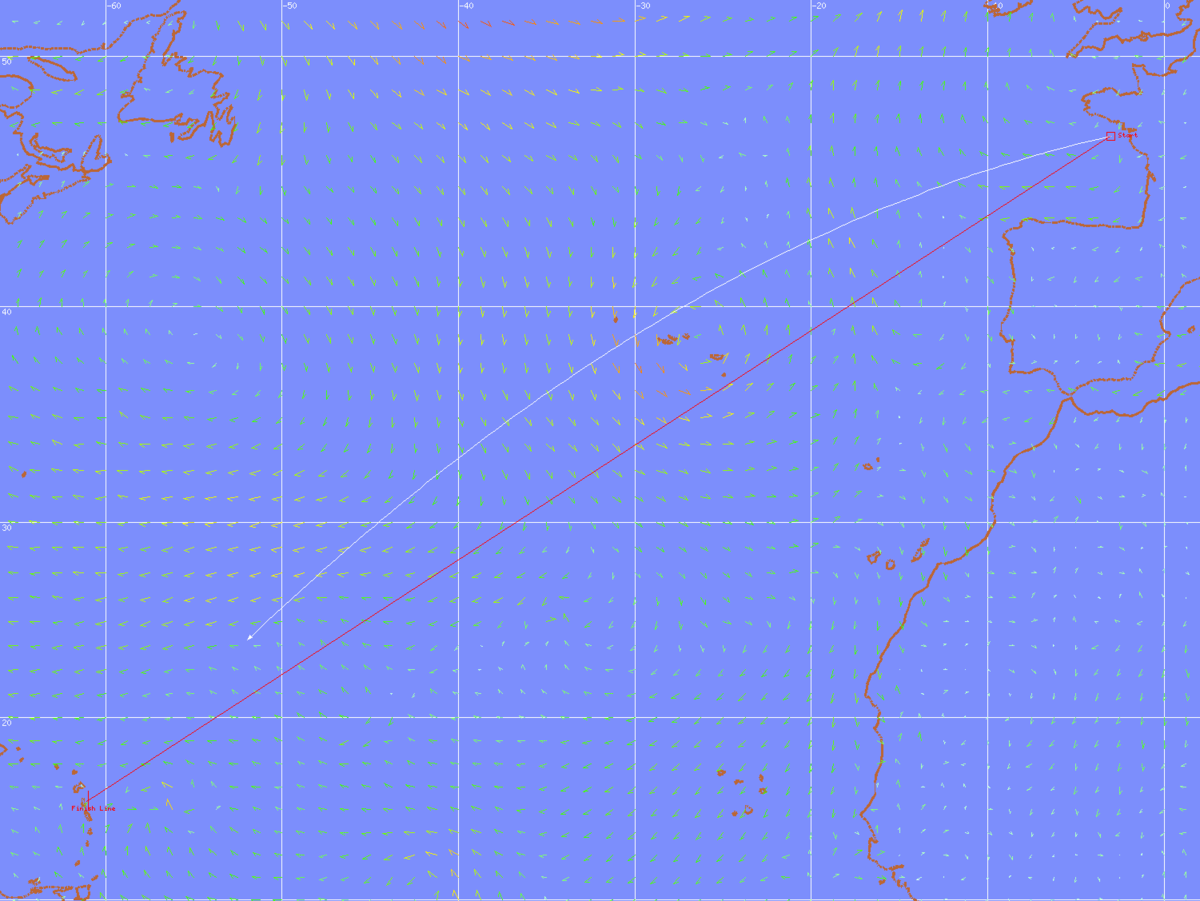
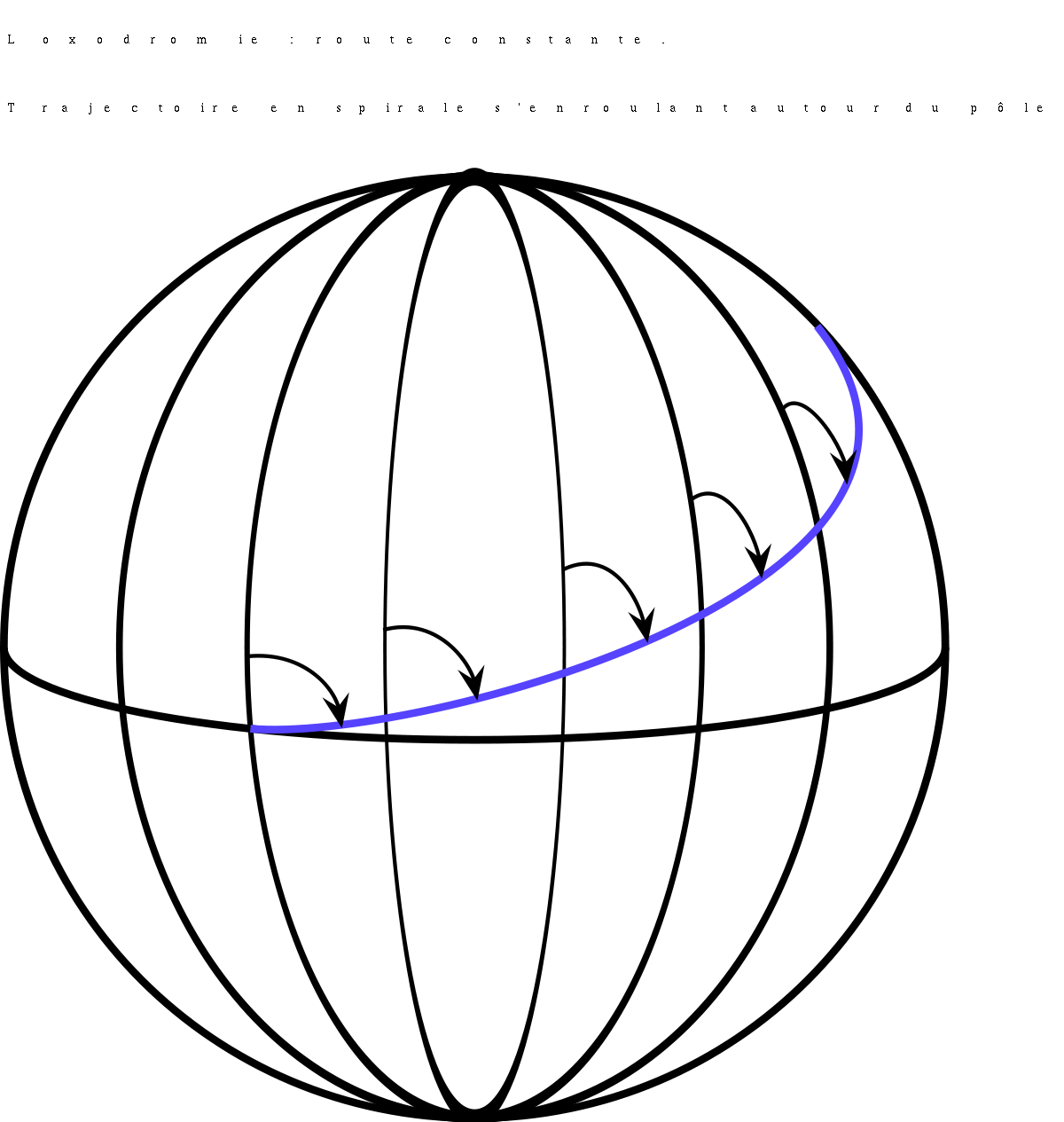
Une loxodromie (du grec lox(o)- et -dromie course oblique), (en anglais rhumb line), est une courbe qui coupe les méridiens d'une sphère sous un angle constant.
Une route loxodromique est représentée sur une carte marine ou aéronautique en projection de Mercator par une ligne droite mais ne représente pas la distance la plus courte entre deux points. En effet, la route la plus courte, appelée route orthodromique ou orthodromie, est un grand cercle de la sphère.
La loxodromie est une trajectoire à route constante. Elle doit son nom au géomètre portugais Pedro Nunes, qui le premier l'a distinguée d'un cercle (c 1537).{Stevin, Harriot l'ont étudiée ( c.1580 ) : c'est un des premiers cas d'"intégration difficile" connus}.
Navigation loxodromique
Le problème posé est celui de la détermination de la route et de la distance loxodromique entre deux points. Il s'agit donc du problème inverse de la navigation à l'estime.
- si les deux points A et B sont peu éloignés, on peut se contenter de formules approchées (latitude moyenne):
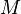
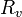
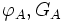
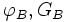
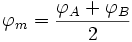
- et :
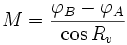
- ces formules approchées restent précises à 1 mille marin près pour
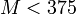
- formules exactes (latitudes croissantes de la projection de Mercator) :
- et :
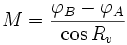
-
-
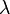
-
-
-
-
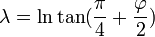
-
-
Démonstration mathématique
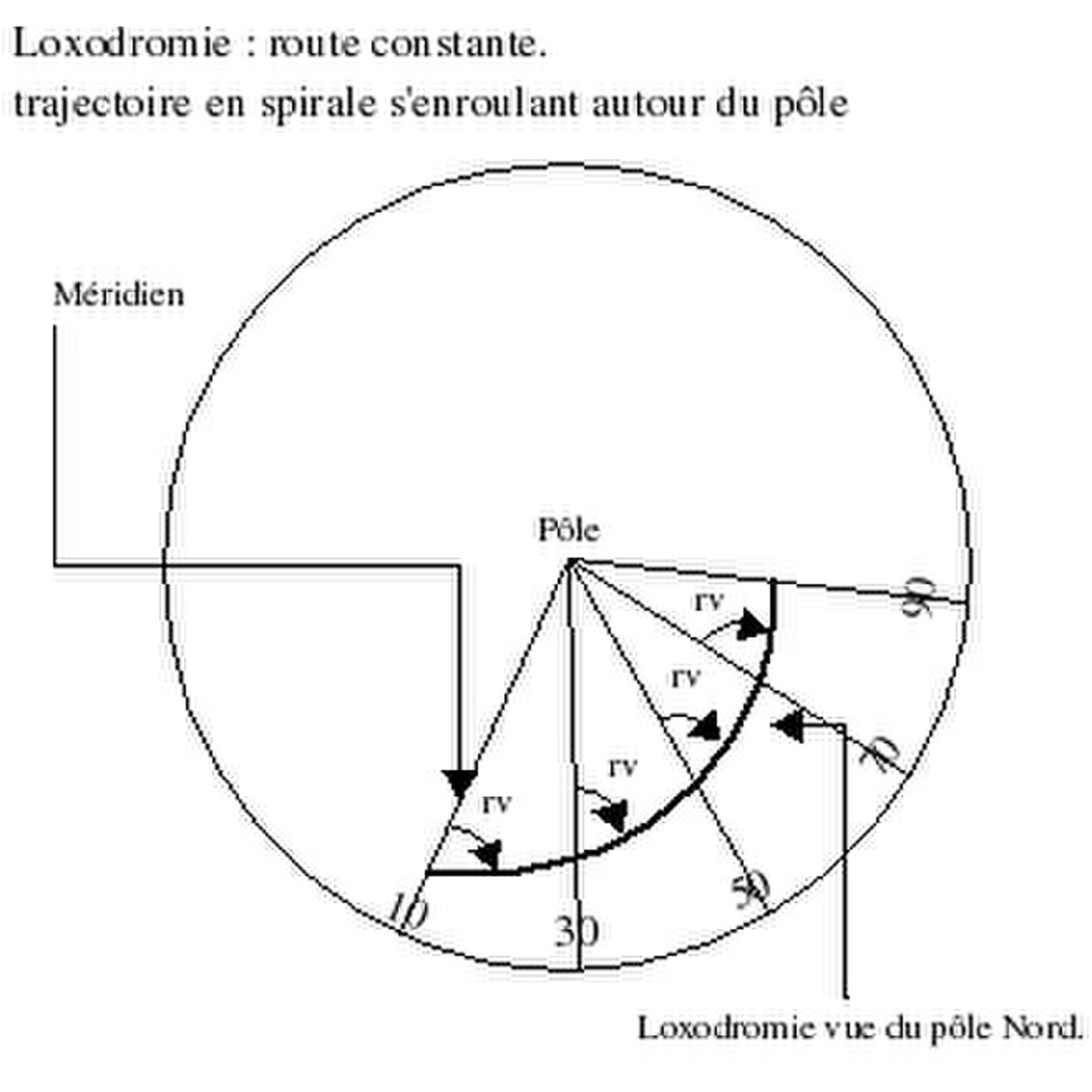
Sur le globe terrestre, les loxodromies correspondent (lorsqu'elles ne sont pas « dégénérées », c'est-à-dire lorsque l'angle initial donné n'est pas nul) à des spirales s'enroulant autour du pôle (le pôle Nord si l'angle initial et dans ]0,π[ et que le déplacement se fait dans le sens des latitudes croissantes).
Soit à déterminer une équation de la loxodromie et à calculer la longueur parcourue à cap constant
![\alpha\in\,]0, \pi[](https://static.techno-science.net/illustration/Definitions/autres/7/70600c5c003bd116139a8aeb2eb3fd44_e914b5751b247ae8b42bb7d27422b85c.png)
Considérons les coordonnées sphériques habituelles sur la sphère unité : la longitude

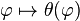
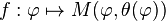


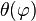


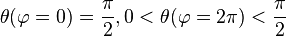
Un vecteur tangent à la loxodromie est ainsi
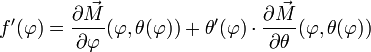
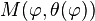
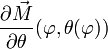
Dans la suite, pour alléger l'écriture, on ne précisera plus le point
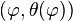
En effectuant le produit scalaire d'un vecteur directeur de la tangente à la loxodromie et d'un vecteur directeur du parallèle, on obtient le produit des normes de ces vecteurs par le cosinus de l'angle qu'ils forment :
-
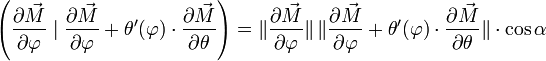
En élevant au carré :
-
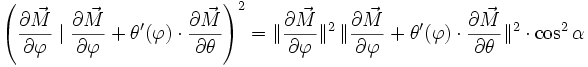
On a d'autre part :
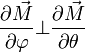
-
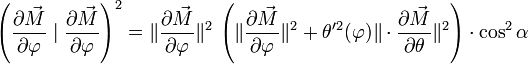
Et en simplifiant :
-
D'où, avec « 1 − sin2 = cos2 »
-
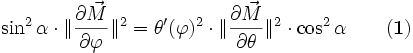
Calculons les deux normes intervenant dans cette équation :
on sait, d'après le paramétrage sphérique rapporté aux coordonnées cartésiennes dans la base
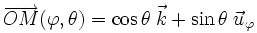
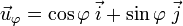
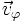

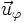
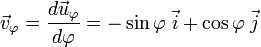
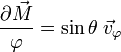
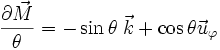
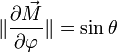
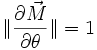
L'équation
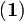
et puisque l'on a supposé un trajet vers le pôle Nord, θ est une fonction décroissante de

![\alpha\in\,]0, \pi/2[](https://static.techno-science.net/illustration/Definitions/autres/3/3d4cafe307f54010cc3ea19e4b0792cf_99d5891e9fc9c5e79f04aeb4f9c6f8e0.png)
-
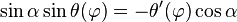
- et
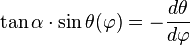
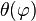
En séparant les variables et en intégrant entre 0 et

-
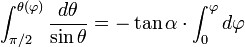
- soit :
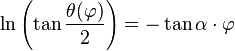
La longueur L parcourue vaut alors, par définition :
-
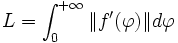
- où
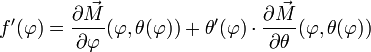
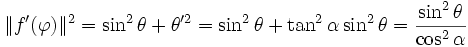
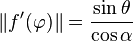
-
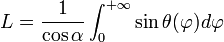
En changeant de variable, avec