Mouvement keplerien - Définition

L'équation de Kepler et son inversion

Durant trois siècles, les mathématiciens se sont préoccupés de trouver theta(t), puisque l'observable la plus facile à repérer est la position du Soleil dans le ciel. Passer de theta à phi et réciproquement est aisé. Par contre s'inverse difficilement (Cf. COLWELL, solving Kepler's equation over three centuries ; ed Willmann-Bell, 1993)

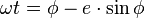
L'article Résolution de l'équation de Kepler donne :

• Le développement de Fourier de phi(t) avec comme coefficients les fonctions de Bessel J_n(ne). Comme φ(t) est une fonction impaire, elle s'exprimera uniquement sur la base réduite des sin (k ωt) :

• Le développement en série de l'excentricité e :

pour e assez petit :

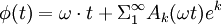
e < E max = 0.662.

Equation du temps de Kepler

Tout cela rappelé, il est évident que celui qui parle du mouvement de Kepler, veut parler de la manière dont la planète se meut sur sa trajectoire.

Certes TOUT est dit dans la deuxième loi de Kepler : la vitesse aréolaire est constante ; il suffit donc de mesurer la date de passage au périgée P, disons t=0, la date actuelle, disons t, de tracer le secteur S(t), POM, de taille pi.a.b.t/T et on aura la position de la planète via le vecteur OM.

Cet article veut expressément aller un peu plus loin, pour ceux qui le désirent.

C'est-à-dire expliciter quelques formules dont les astronomes ont besoin pour tracer ce fameux secteur S(t) ; car si la phrase précédente est exacte, elle recouvre pas mal de calculs plus délicats et des problèmes de recherche actuels non résolus, malgré l'ancienneté du problème.

• En effet, les équations du mouvement sont plus difficiles.

L'habitude est de passer par l'anomalie excentrique (:= phi) :

elle est reliée à theta angle polaire par la relation : .

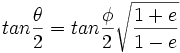
(un peu de géométrie permet de le démontrer ; on vérifiera les cas particuliers simples).

Et TM := .

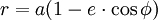
En un tour, de durée T, phi varie de 2Pi :

.

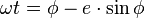
Cette formule s'appelle équation du temps de Kepler

Rappel : la pulsation w = 2.Pi/T dépend de a mais pas de l'excentricité e, donc se calcule via un mouvement circulaire :

.(troisième loi de Kepler)

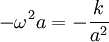
Les échelles de temps et dualité

la dualité (r & φ) et (u & θ) est directement liée aux échelles de temps (Cf. échelle de temps en mécanique classique).

• En effet, la loi des aires étant connue, il apparaît logique de prendre comme échelle de temps . Alors il vaut mieux choisir u : = 1/r comme fonction inconnue ; c'est la méthode de Clairaut-Binet, avec l'anomalie vraie (l'angle polaire).

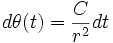
• Mais tout aussi logique est l'échelle de temps . Alors ce qui convient le mieux est la fonction inconnue r : c'est la méthode de l'anomalie excentrique.

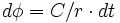
• Assez curieusement, ce changement de dt intervient aussi dans le phénomène d'aberration de la lumière traité en mécanique relativiste. L'explication, assez subtile, est : les deux sont reliés à SO(3,1)

Évidemment, on pense aussi à . Cela correspond-il à quelque « réalité » géométrique ? la réponse est oui ! l'Hodographe est un cercle avec le centre de force à l'intérieur. Cet Hodographe est parcouru selon la loi des aires ! et ψ est le bon paramétrage.

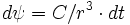
• Remarque : Tout ceci est lié avec des calculs de moyenne de (1/r)^k en mécanique quantique de l'atome d'hydrogène.

Dans l'article échelle de temps en mécanique classique, est discuté un autre aspect de ces changements d'échelle.