Mouvement keplerien - Définition

Quelques démonstrations géométriques historiques

Il a été proposé douze démonstrations historiques que l'on pourra retrouver sous un autre article, par souci de clarté.

Perturbations du mouvement keplerien

Evidemment ce qui est intéressant dans la réalité est le mouvement réel des planètes, qui se perturbent l'une l'autre.

De même dans le cas des satellites artificiels, on peut tirer beaucoup de renseignements par la géodésie spatiale, sur la forme exacte de la Terre et son évolution.

Pour des raisons de taille, cela est reporté à un article ultérieur.

Hooke et Kepler, ou de Thomson à Rutherford

z->z² dans le plan complexe de la trajectoire est aussi une très jolie démonstration, très proche sans doute de celle du deMotu. La présentation sera celle de V.I. Arnold (1990, ed Birkhauser). Voir aussi Needham (Visual Complex Analysis). Goursat (CRAS,1889)

Partir de la définition de la Hire d'une ellipse (H), [H, pour Hooke] :

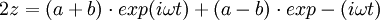
C'est une ellipse de Hooke, parcourue sous l'action de l'accélération centrale : .

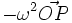
Effextuons la transformation conforme Z = z² :

.

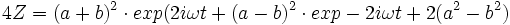
C'est encore une ellipse de la Hire, la dénommer (K) [K pour Kepler] ! mais d'excentricité différente E = C/A = c²/ab, et cette fois, le point O est le FOYER de l'ellipse. D'autre part, la période de l'orbite est T/2 !

Elle est encore décrite selon la loi des aires par rapport à O ! et donc d'après Clairaut-Binet-Siacci-Hamilton la force est newtonienne !

Prenons comme loi de force celle de la théorie de Thomson (théorie dite de l'électron élastiquement lié). La simple transformation conforme Z = z² la transmute en la théorie de Rutherford de l'électron planétaire autour d'un noyau central.

Conséquences quantiques

Pauli (1925) a vite compris le parti qu'il pouvait tirer de cette correspondance : son camarade, Heisenberg, venait de quantifier l'oscillateur harmonique, facilement généralisable en 3D. Il restait à faire « Z = z^2 ».

C’est-à-dire à comprendre les symétries de l'oscillateur 3D et celle de l'atome d'hydrogène. Évidemment il trouva comme invariant L, le moment cinétique ; mais aussi le vecteur excentricité E (« perpendiculaire à L »).

Pour une énergie négative, cela correspondait à une symétrie SO(4), et pour une énergie positive à une symétrie SO(3,1) qu'il connaissait bien, puisqu'il s'agit du groupe des transformations de Lorentz, qu'il avait si bien décrit à l'âge de vingt-et-un ans dans la célèbre Handbuch der Physik, et dont les générateurs infinitésimaux étaient bien connus (les six rotations infinitésimales dans l'espace de Minkowski donnent (Cf. Jackson, Electromagnétisme, ed Dunod, 2000 ou bien Goldstein, mécanique classique) le moment cinétique généralisé ( L, K) avec L. K = 0. Il en résulte une résolution immédiate et élégante de l'équation de Schrodinger, analogue quantique de celle de Hermann (1710) (voir Théorie de Pauli de l'atome d'hydrogène).

D'autre part le Z= z² se traduit par le fait que les Polynômes d'Hermite orthogonaux avec une densité de mesure en exp-(x^2+y^2+z^2). dx dy dz = r^2.exp-r^2 .dr se retrouvent en correspondance avec les polynômes de Laguerre orthogonaux avec une densité de mesure en exp(-r. dr). Bander & Itzykson (Rev.Mod.Phys 1966,38,330-345) passent en revue cet aspect inattendu de la correspondance Hooke-Kepler.

Évidemment, pour une énergie positive, la symétrie de groupe est celle de SO(3,1), ce qui brouille quelque peu les cartes : le spectre continu de l'atome d'hydrogène n'est pas aussi simple que son spectre discret, non plus que les fonctions propres.