Optique géométrique - Définition

Quelques applications

Succession de dioptres

La succession de deux dioptres plans non parallèles constitue un prisme, dont les propriétés de réflexion totale ou de dispersion (faculté de séparer les différentes longueurs d'onde) en font un objet largement utilisé. (Actuellement, pour ce qui est de la dispersion, il est supplanté par les réseaux (optique physique)).

La succession de deux dioptres dont l'un est sphérique (ou cylindrique) constitue une lentille.

Les instruments d'optique

• La loupe

La loupe est l'instrument d'optique réfractant le plus simple : elle est constituée d'une unique lentille convergente.
Son utilisation repose sur la possibilité d'obtenir une image, de même sens que l'objet, (droite et virtuelle) : des détails de l'objet sont alors vus sous un angle plus grand qu'il ne pourraient l'être à l'œil nu. Pour cela il faut que l'objet soit situé à une distance de la loupe inférieure ou égale à la distance focale.

• L'appareil photographique

Le principe de l'appareil photographique est également des plus simples : une seule lentille convergente (en réalité une combinaison savante et complexe - souvent secrète - de plusieurs lentilles réelles), qui donne de l'objet une image réelle recueillie sur un écran. Dans ce cas, l'image est généralement plus petite que l'objet. Seule particularité de cet instrument, il nécessite un récepteur sensible à la lumière pour enregistrer l'image. Ce récepteur peut être une pellicule contenant des sels d'argent photosensibles (procédé chimique de la photo dite argentique) ou une cellule photosensible (CCD) (procédé physique de la photo dite numérique).

• Télescope de Newton

Il s'agit d'un système afocal constitué d'un miroir parabolique ou sphérique de grand diamètre chargé de collecter la lumière provenant des étoiles, suivi d'une lentille de plus courte focale (l'oculaire) servant de loupe pour regarder l'image intermédiaire. L'astuce du télescope de Newton est d'interposer un petit miroir plan qui permet de placer l'oculaire à 90°.

• Lunette astronomique

Il s'agit d'un système afocal constitué d'une lentille de grand diamètre et de grande distance focale (l'objectif) chargée de collecter la lumière provenant des astres, suivie d'une lentille de courte distance focale (l'oculaire) servant de loupe pour regarder l'image intermédiaire.

Remarque : la lunette astronomique donne une image renversée. Elle est donc peu adaptée à l'observation des objets terrestres. On utilise la lunette dite « terrestre » ou lunette de Galilée, instrument ayant un objectif mais utilisant une lentille divergente comme oculaire : de la sorte, l'image finale est droite.

• Microscope

Le principe du microscope optique est d'obtenir une image très agrandie d'un objet réel, de faible dimension, situé à distance finie, grâce à une lentille, de très courte focale, appelée objectif, et d'observer à l'aide d'une loupe (en fait un oculaire puissant) cette image agrandie : cet instrument emploie donc deux lentilles convergentes.

Définitions et lois fondamentales de l'optique géométrique

L'optique géométrique consiste à étudier la manière dont la lumière se propage en ne considérant que la marche des rayons.

L'optique géométrique repose sur deux lois fondamentales :

• Propagation rectiligne de la lumière : dans un milieu transparent, homogène et isotrope, la lumière se propage en ligne droite : les supports des rayons sont des droites.
• Principe du retour inverse de la lumière : si la lumière suit un trajet quelconque d'un point A à un point B (y compris dans un système optique), alors la lumière peut suivre exactement le trajet inverse de B vers A. Autrement dit, le sens de parcours change, mais pas les directions.

On appelle dioptre la surface séparant deux milieux transparents. Les rayons demeurent rectilignes dans un milieu homogène et isotrope ; ils sont, généralement, déviés lors du franchissement d'un dioptre ou à la rencontre d'une surface réfléchissante. Le changement de direction aux interfaces est décrit par les lois de Snell-Descartes.

Lois de Snell-Descartes

On considère un rayon se propageant dans un milieu homogène et isotrope d'indice de réfraction n₁, et tombant sur une surface (dioptre ou surface réfléchissante). Le plan d'incidence est le plan qui contient le rayon incident et la normale à la surface au point d'incidence. L'angle d'incidence est l'angle formé par le rayon d'incidence et la normale à la surface.

Si le rayon lumineux tombe sur une surface réfléchissante, il est dévié. Le rayon réfléchi reste dans le plan d'incidence et sa direction de propagation est telle que l'angle de réflexion est égal à l'angle d'incidence. Ce phénomène est connu depuis les travaux de Ptolémée, Alhazen ou Kepler, de même que, qualitativement, la déviation au franchissement d'un dioptre.

Lorsque le rayon lumineux tombe sur une surface séparant le milieu où il se propage ( milieu d'incidence ) d'un autre milieu, d'indice de réfraction n₂, il donne naissance, dans ce second milieu, à un rayon qui n'est pas dans son prolongement (sauf à l'incidence normale) : c'est le rayon réfracté. Snell et Descartes ont montré, indépendamment, que dans le cas où les deux milieux sont homogènes et isotropes, la réfraction suivait une loi « simple » en sinus.

Au niveau de l'interface :

1. Les rayons lumineux réfléchis sont dans le plan d'incidence, et tels que l'angle de réflexion est égal à l'angle d'incidence.
2. Les rayons lumineux transmis sont dans le plan d'incidence, et tels que l'angle de réfraction est lié à l'angle d'incidence par la formule

où n₁ est l'indice du milieu d'incidence, n₂ celui du milieu de réfraction, θ₁ l'angle d'incidence et θ₂ l'angle de réfraction. De plus, l'indice dépend généralement de la longueur d'onde de la lumière incidente et la réfraction conduit alors à la dispersion d'une lumière polychromatique. Le rayon réfléchi (ou réfracté) et le rayon incident se situent de part et d'autre de la normale.

Remarque 1 : les deux phénomènes, réflexion et réfraction peuvent, évidemment, être expliqués dans le cadre de l'Optique ondulatoire.

Remarque 2 : ces lois peuvent aussi s'obtenir dans des milieux non homogènes par l'intermédiaire du Chemin optique

Remarque 3 : Il existe un angle d'incidence limite tel que , cette notion d'angle limite intervient surtout dans le phénomène de fibre optique.

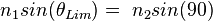
Stigmatisme et notion d'image optique

Un système est dit rigoureusement stigmatique lorsque tous les rayons issus d'un point (source isogène) et traversant le système ont tous leurs supports concourants.

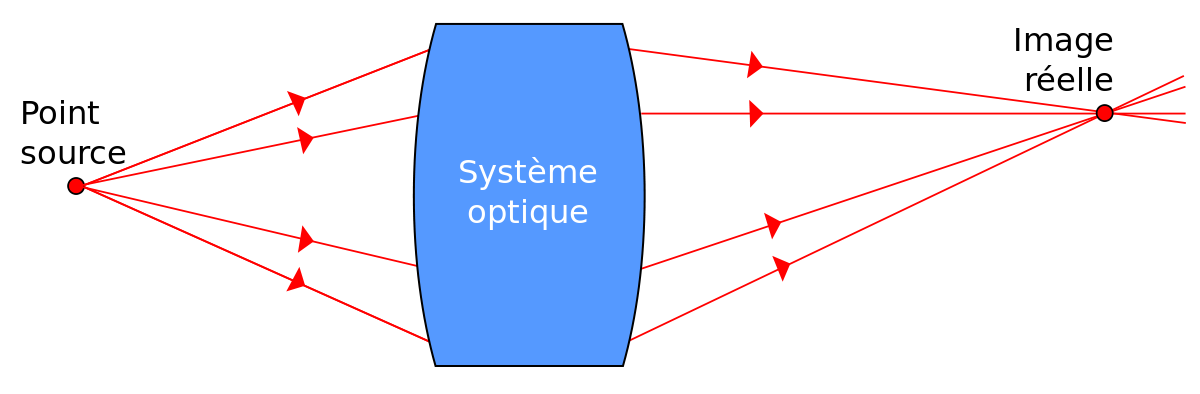
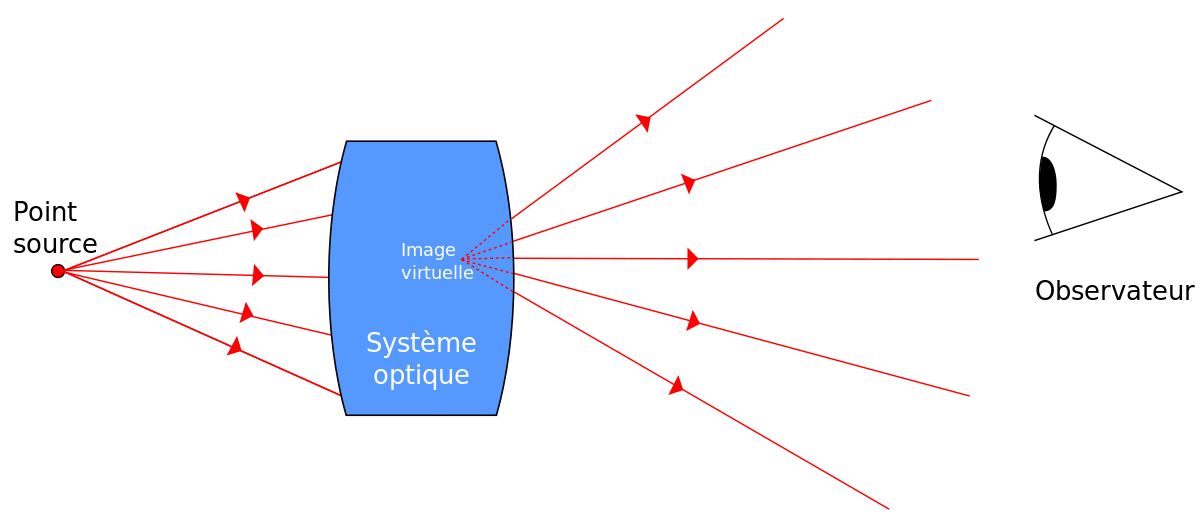
Le point image est dit réel s'il est situé en aval de l'élément optique par rapport au sens de propagation de la lumière. Il est dit virtuel s'il est situé en amont de la face de sortie de l'élément optique par rapport au sens de propagation de la lumière. Inversement, un point objet est réel s'il est situé en amont de l'élément optique par rapport au sens de propagation de la lumière et virtuel s'il est situé en aval de la face d'entrée de l'élément optique par rapport au sens de propagation de la lumière.

La propriété dite de stigmatisme est étroitement liée à la définition d'image optique. Pour un objet donné, un système optique n'en donne une image (stricto sensu) que s'il est stigmatique pour tous les points de l'objet. Dans ce cas, chaque point de l'objet a un point image et l'objet lui-même a donc une image.

Dans la pratique cette propriété est rarement réalisable. On est amené à parler de stigmatisme approché lorsque les rayons convergent presque en un même point, c'est-à-dire lorsque la zone de convergence a une taille inférieure à la résolution de notre vue (aptitude à distinguer deux points objets voisins : typiquement, dans des conditions optimales de contraste et d'éclairement, l'œil humain peut séparer, à une distance de 10 m, deux points écartés de 3 mm : on parle de pouvoir séparateur ou de résolution de la vue).

Stigmatisme rigoureux du miroir plan

Dans la figure ci-contre, ont été représentés quelques rayons issus d'un objet lumineux réel et venant se réfléchir sur le miroir (que l'on schématise par un segment muni de hachure à l'arrière) selon les lois de Snell-Descartes.

Un observateur, et ce, quelle que soit sa position dans le faisceau réfléchi, recevra de la lumière qui lui semble provenir d'un point symétrique de l'objet par rapport au plan du miroir : l'image (virtuelle) que l'observateur voit.

Cette image est symétrique de l'objet par rapport au plan du miroir et a la même taille (grandissement = 1). Elle est virtuelle, car elle est située en amont du miroir si on considère le sens de propagation des rayons réfléchis.

Stigmatisme approché du dioptre plan

Il est facile de vérifier avec un papier et un crayon (et une calculatrice) que la réfraction fait du dioptre plan un système non-stigmatique : les rayons issus d'un point, traversant le dioptre, donnent un ensemble de réfractés qui ne se coupent pas tous au même point.

L'illustration ci-dessus montre que la lumière issue d'un point placé dans un aquarium, par exemple, donne des rayons réfractés dans l'air qui ont des directions sans point commun.

Pourtant, on lit parfaitement un journal placé à plat au fond d'une baignoire remplie d'eau (si l'eau n'est ni agitée, ni troublée). C'est donc qu'un point sur un i, par exemple, constitue un objet qui forme une image de bonne qualité sur la rétine de l'œil de l'observateur. Ceci n'est possible que parce que le faisceau de lumière, tombant sur notre pupille, est suffisamment étroit, du fait de la faible dimension de cette pupille. Ainsi les rayons, issus du point sur le i - supposé, en toute rigueur, coloré ! -, qui atteignent la rétine, y forment, après réfraction, une tache assez petite pour que notre cerveau l'assimile à un point. On est bien alors dans un cas de stigmatisme approché ; si la tache est inférieure à la résolution de notre œil : l'image semble nette. Si la tache est plus grande, l'image est floue. C'est pour cette raison qu'un « gros'œil » de dinosaure ne pourrait lire le journal immergé... mais la question ne se pose pas puisqu'au jurassique la presse n'existait pas ! (ni sans doute la baignoire).

Remarque : l'image obtenue par réflexion sur un miroir plan est localisée indépendamment de la position de l'observateur ; au contraire, l'image approchée obtenue par réfraction dépend de la position de ce dernier. On l'observera, au bord d'une piscine, en se déplaçant légèrement : le reflet du bord est « fixe » tandis que le fond semble un « tapis volant » se mouvant au gré des déplacements de l'observateur.

Systèmes centrés : image d'un objet étendu - aplanétisme

Très souvent les éléments d'un système optique ont une symétrie de révolution. On parle de système centré lorsque les différents éléments ont un axe de symétrie commun : l'axe principal .

Un tel système est alors défini par ses éléments cardinaux - foyers et plans principaux, notamment, permettant de définir les distances focales et de construire les images.

Un objet n'est généralement pas ponctuel : on parle alors d'objet étendu. Le stigmatisme pour un point, qu'il soit rigoureux ou approché, ne garantit pas l'obtention de l'image d'un objet quelconque. Lorsque le stigmatisme est conservé au voisinage d'un point et dans un plan perpendiculaire à l'axe optique, on dit que le système est aplanétique. L'image d'un petit objet perpendiculaire à l'axe est alors dans le plan perpendiculaire à l'axe contenant les images des points constituant l'objet.

Dioptres et miroirs quelconques

Il faut insister sur le fait que les lois, précédemment définies, n'exigent en rien la planéité de l'interface : ce sont des lois locales applicables si l'on peut définir une normale à l'interface au point où le rayon l'atteint (point d'incidence).

Les lois de Snell-Descartes s'appliquent donc lorsque les surfaces sont non-planes. L'application des lois de la réflexion et de la réfraction permettent alors de tracer le devenir de tout rayon incident, donnant ainsi des informations sur la géométrie du faisceau réfléchi et (ou) du faisceau réfracté.

La figure ci-contre donne un exemple dans le cas d'un dioptre concave, où le milieu de réfraction (en bleu) est plus réfringent que le milieu d'incidence.

Le cas du dioptre sphérique est particulièrement important puisqu'il limite les faces des lentilles les plus couramment et les plus anciennement employées, car, techniquement par usure et polissage, les plus faciles à réaliser.

Pour les miroirs, ce sont, en plus des miroirs plans, les miroirs sphériques et les miroirs paraboliques (réflecteurs des phares de voitures, par exemple) les plus utilisés.