Polynôme minimal d'un endomorphisme - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le polynôme minimal est un outil qui permet d'utiliser des résultats de la théorie des polynômes à l'algèbre linéaire. Il est en effet possible d'appliquer un polynôme à un endomorphisme, comme expliqué dans l'article intérêt du concept de polynôme d'endomorphisme.
Il est défini comme le polynôme normalisé (son coefficient de plus haut degré est égal à 1) de plus petit degré qui annule un endomorphisme c'est-à-dire une application linéaire d'un espace vectoriel dans lui-même.
Il est utilisé essentiellement en dimension finie ; il joue un rôle important dans la réduction d'endomorphisme. Il dispose de propriétés fortes dont la plus célèbre est probablement le théorème de Cayley-Hamilton.
Les démonstrations associées au polynôme minimal se trouvent essentiellement dans l'article Polynôme d'endomorphisme qui approfondit ce concept dans un cadre théorique plus large.
Il existe un cas particulier, utilisé dans le cadre de la théorie de Galois et la théorie algébrique des nombres appelée polynôme minimal d'un nombre algébrique.
Définition
On suppose que E est un espace vectoriel de dimension finie et égale à n. Soit u un endomorphisme de E. Nous avons la définition suivante:
-
- Le polynôme minimal de l'endomorphisme u est le polynôme unitaire de plus petit degré qui annule u.
Approche par l'exemple
Considérons le cas où n est égal à 2, où l'espace vectoriel est réel, ce qui signifie que les multiplications scalaires des vecteurs ont lieu sur les réels. Soit un endomorphisme u ayant la représentation matricielle suivante dans une base (e1, e2):
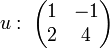
Calculons alors la représentation matricielle du carré de u, on trouve:
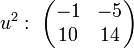
Existence du polynôme minimal
On peut alors remarquer qu'il existe une relation de dépendance linéaire entre u2, u et Id l'endomorphisme identité. En effet:
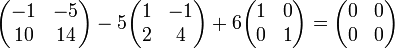
Ce qui nous montre l'existence du polynôme minimal que nous notons
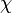
![\chi[X]=X^2-5X+6=(X-2)(X-3)\;](https://static.techno-science.net/illustration/Definitions/autres/4/478415f3d691ac3366050714da1e0d73_e02497cf1c66063b720edeb168b880d3.png)
Dans cet exemple, nous avons montré l'existence du polynôme minimal et nous avons montré que son degré est égal à la dimension de l'espace vectoriel. Cette propriété est générale en dimension finie, le polynôme minimal existe toujours et son degré est inférieur ou égal à la dimension de l'espace.
Valeurs propres et racines
Un vecteur propre est un vecteur non nul dont l'image par l'endomorphisme lui est proportionnelle. Une des propriétés du polynôme minimal réside dans le fait que ses racines sont les valeurs propres. Recherchons alors des vecteurs propres en utilisant cette propriété. Pour la valeur propre 2, on trouve:
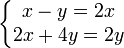
En résolvant ce système nous obtenons x = − y. En posant x = λ , nous obtenons y = − λ, qui est la description paramétrique de tout vecteur propre. En choisissant λ = 1, nous obtenons le vecteur propre (1,-1)
On peut vérifier de même que
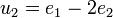
Polynôme minimal et diagonalisation
Nous disposons de deux vecteurs propres u1 et u2 qui forment une famille libre dans un espace de dimension 2, ils constituent donc une base. Nous pouvons alors remarquer que dans cette base, l'endomorphisme s'exprime sous la forme:
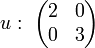
Une telle matrice possède des termes tous nuls en dehors de la diagonale. Cet exemple illustre une propriété importante du polynôme minimal. L'endomorphisme est diagonalisable si et seulement si le polynôme possède toutes ses racines et qu'aucune de ses racines ne soit multiple.
Polynôme minimal et polynôme caractéristique
Le polynôme caractéristique correspond au déterminant de l'application
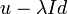
![P[X]=\begin{vmatrix} 1-X & -1 \\ 2 & 4-X \end{vmatrix}=(1-X)(4-X)+2=X^2-5X+6](https://static.techno-science.net/illustration/Definitions/autres/7/76618a6650fbb8f0a7fe4cc474dedd48_3561a89227f79f40d0d40235e51caf48.png)
Le polynôme caractéristique est dans ce cas égal au polynôme minimal. Dans le cas général, le polynôme minimal divise toujours le polynôme caractéristique mais l'égalité n'est pas systématique.

















































