Pouvoir d'arrêt (rayonnement ionisant) - Définition

Introduction

Pouvoir d'arrêt de l'aluminium pour les protons, en fonction de l'énergie des protons.

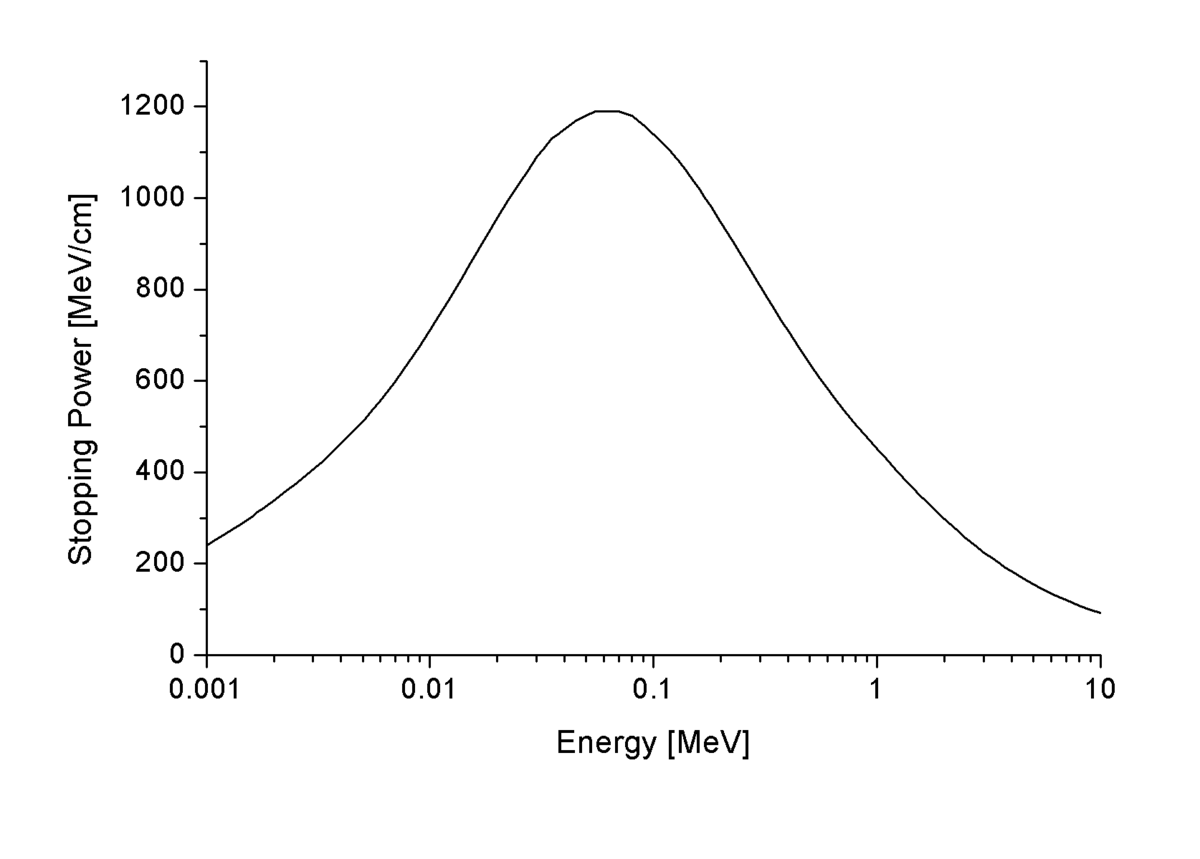
En traversant la matière, les particules chargées energétiques ionisent les atomes ou molécules sur leur parcours. Par conséquent, les particules perdent peu à peu leur énergie. Le pouvoir d'arrêt est la perte moyenne d'énergie de la particule par distance parcourue, mesurée par exemple en MeV/cm (voir la figure ci-contre).

Pouvoir d'arrêt et parcours

Le pouvoir d'arrêt dépend du type de particule, de son énergie et des propriétés de la matière traversée. Car la production d'un paire d'ions (typiquement un ion positif et un électron) requiert une quantité fixe d'énergie (par exemple, à peu près 33 eV pour l'air), la densité d'ionisation est proportionnelle au pouvoir d'arrêt du matériau.

Les électrons, les ions atomiques, les mésons etc. perdent tous de l'énergie en traversant la matière. Ici, nous considérons surtout des ions atomiques.

Le pouvoir d'arrêt mesure une propriété du matériau, tandis que la perte d'énergie par cm considère la situation du point de vue de la particule. Mais la valeur et les unités sont les mêmes et cette valeur est normalement positive, à cause du signe moins devant la définition suivante:

La courbe Bragg pour les particules alpha de 5,49 MeV dans l'air

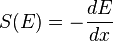
où E est l'énergie, et x est la distance parcourue. Le pouvoir d'arrêt, et par conséquent la densité d'ionisation, croissent normalement avec la décélération: c'est la courbe Bragg, nommée d'après William Henry Bragg. Un peu devant la fin du parcours, la perte d'énergie passe par un maximum, le pic de Bragg. Ce pic est primordial en radiothérapie.

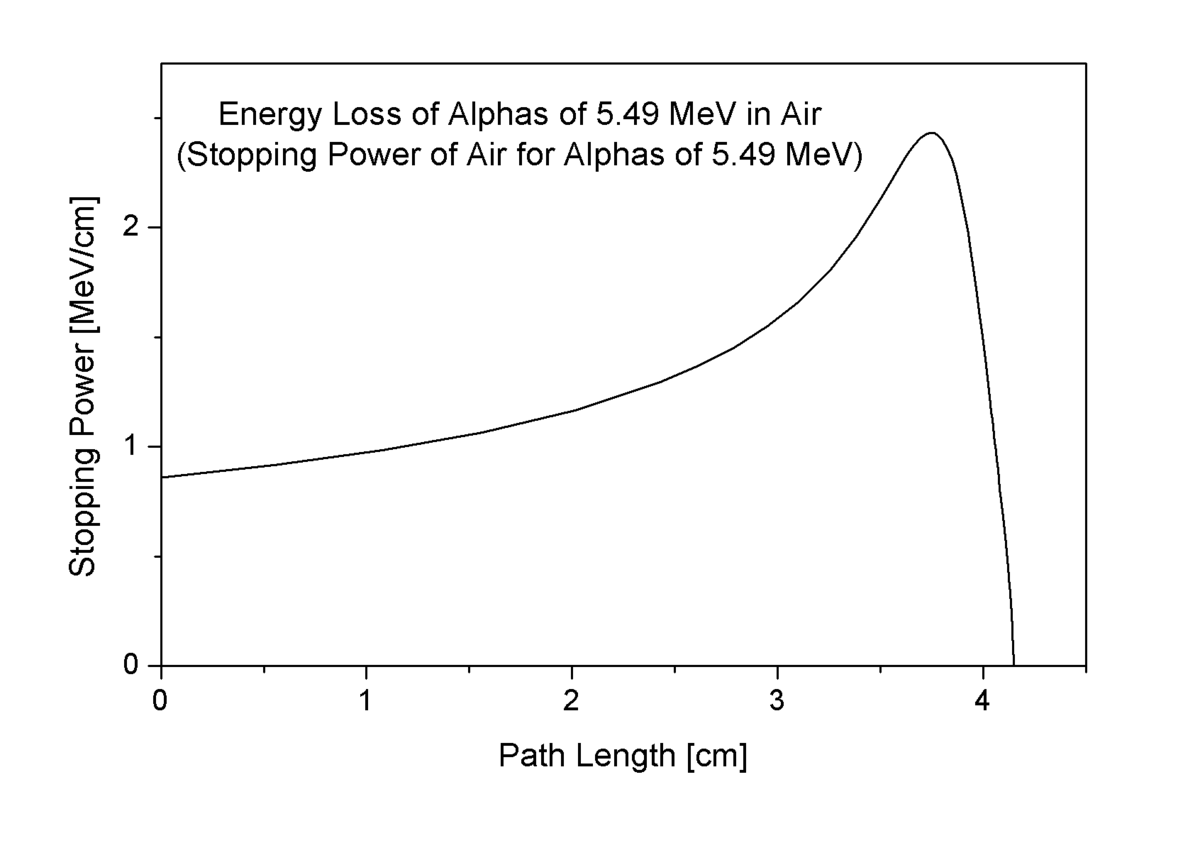
Dans la figure ci-contre, on voit que le pouvoir d'arrêt des particules α de 5,49 MeV dans l'air monte avant d'atteindre un maximum (cette énergie correspond à la désintégration α du gaz radon ²²²Rn qui est présent dans l'atmosphère des lieux aux sols granitiques).

L'équation au-dessus définit le pouvoir d'arrêt linéaire qui peut être exprimé en unités comme MeV/mm, par exemple. Très souvent, S(E) est divisé par le densité du matériau; de cette manière-là, on arrive au pouvoir d'arrêt de masse qui peut être exprimé en unités comme MeV/(mg/cm²), par exemple. Le pouvoir d'arrêt de masse ne dépend pas de la densité, approximativement.

On peut calculer le parcours moyen en intégrant la réciproque du pouvoir d'arrêt S(E) sur la quantité d'énergie.

Absorption de divers faisceaux par l'eau : en bleu et orange, des courbes de Bragg pour les protons à 250 MeV, en rose l'absorption de rayons gamma passant par la Crête de Tavernier.

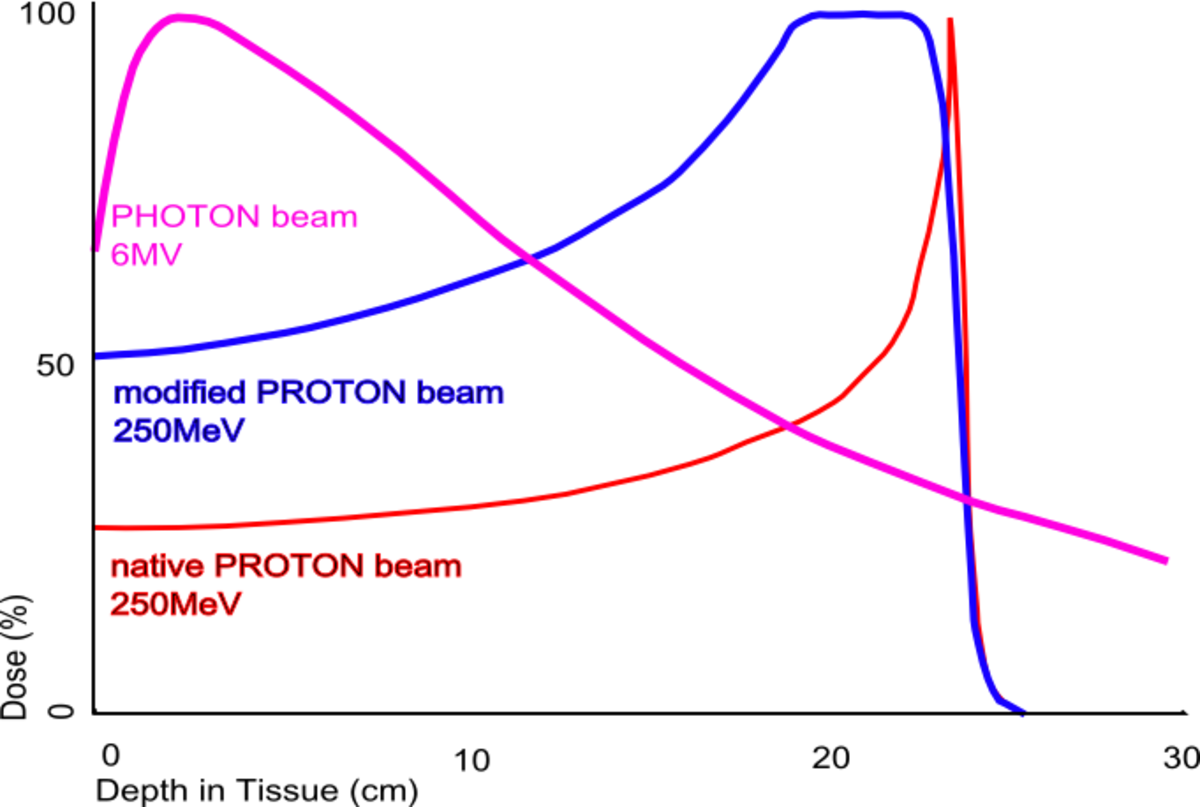
La figure à gauche montre l'absorption par l'eau d'un faisceau de protons accélérés à 250 MeV (courbe orange); cette courbe a un pic très aigu. Pour irradier une tumeur plus épaisse en radiothérapie, on peut élargir cette pointe en modifiant l'énergie de l'accélérateur ou en utilisant de matériau absorbant(courbe bleue).

Cette figure montre également l'absorption d'un faisceau de photons de haute énergie (courbe rose). Cette courbe est tout à fait différente. Elle a essentiellement une décroissance exponentielle après un passage par un maximum appelé Crête de Tavernier du nom du physicien belge Guy Tavernier qui découvrit le phénomène en 1948. Cette allure de courbe est d'ailleurs aussi semblable pour les faisceaux de neutrons et les rayons X et Gamma. Le photon ne perd pas son énergie progressivement par des ionisations successives, mais il perd souvent toute son énergie en une seule ionisation. L'absorption de photons n'est pas décrite par le pouvoir d'arrêt, mais par un coefficient d'absorption.