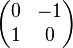Pseudovecteur - Définition

Représentation matricielle

Un pseudovecteur peut être représenté par un tenseur antisymétrique d'ordre 2, qui correspond à la représentation d'un tenseur. Avec 3 possibilités : soit le tenseur est 2 fois contravariant, soit 1 fois contravariant-1 fois covariant, soit 2 fois covariant ; seul le 2^e cas correspond à une matrice usuelle, où l'action d'un tel tenseur sur un vecteur donne à nouveau un vecteur.

Dans ce cas, en base orthonormale, la matrice :

,

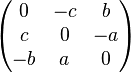
correspond au pseudovecteur usuellement représenté par :

.

On peut aussi représenter les deux autres types de pseudovecteurs sous forme matricielle, mais ils réagissent aux changements de base comme des formes bilinéaires ou des aires.

Cette représentation par matrice carrée est particulièrement adaptée car

• le produit vectoriel avec un vecteur vrai se traduit par une simple multiplication matricielle (attention cependant au signe, et à l'ordre des facteurs) ;
• le produit vectoriel avec un autre pseudovecteur se traduit par le crochet de Lie des deux matrices. [A, B] = AB - BA ; il est nul si et seulement si les deux matrices commutent.
• Les changements de base sont identiques aux changements de base des tenseurs d'ordre 2, voire à ceux des matrices quand il s'agit d'un tenseur 1 fois contravariant-1 fois covariant ;
• elle permet de voir facilement qu'un pseudovecteur correspond à une matrice de rotation d'un quart de tour dans un plan suivie ou précédée d'une projection sur ce plan ;
• en dimension 2, le produit vectoriel des deux vecteurs de base du plan correspond à une matrice antisymétrique :

Avec cette matrice, on peut représenter les nombres complexes. Le produit matriciel de cette matrice avec elle-même donne en effet l'opposé de la matrice identité. Et elle permet aussi par combinaison linéaire, de représenter les similitudes planes directes.

Exponentielle

L'exponentielle de la matrice qui représente des pseudovecteurs (1,1) en dimension 3 est une matrice de rotation, d'angle (en radian) , dont la direction est donnée par le pseudovecteur.

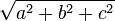
Règles de calcul

On portera attention au fait que si les calculs sont effectués en base orthonormée, il peut y avoir confusion entre vecteur/covecteur/pseudovecteur. Ces règles de calcul peuvent servir à lever les ambiguïtés et pouvoir alors changer de base.

Produit vectoriel

• Si a est un vecteur vrai et b un vecteur vrai, l'objet p tel que est un pseudovecteur.
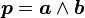
• Si a est un vecteur vrai et b un pseudovecteur, l'objet p défini comme précédemment est un vecteur vrai.
• De même, si a est un pseudovecteur et b un vecteur vrai, l'objet p défini comme précédemment est un vecteur vrai (c'est le cas du vecteur de Poynting en électromagnétisme).
• Si a et b sont des pseudovecteurs, l'objet p défini comme précédemment est un pseudovecteur

Addition

• L'addition ou la soustraction de deux pseudovecteurs est un pseudovecteur ;
• L'opposé d'un pseudovecteur est un pseudovecteur ;
• On n'additionne pas un pseudovecteur avec un vecteur ou un covecteur.
• On n'additionne pas des pseudovecteurs de types différents.

Multiplication par un scalaire vrai

• La multiplication d'un pseudovecteur par un scalaire vrai est un pseudovecteur de même type;
• La multiplication d'un vecteur vrai par un scalaire est un vecteur vrai.
• Par scalaire vrai, il faut comprendre un nombre totalement indépendant de la base des vecteurs. Dans ce cas là, on ne peut pas considérer le travail d'une force ou énergie par exemple comme un scalaire, puisque cette grandeur est doublement contravariante.

Produit scalaire

• Le produit scalaire d'un vecteur vrai et d'un covecteur est un scalaire vrai
• Le produit scalaire d'un pseudovecteur doublement contravariant et d'un pseudovecteur doublement covariant est un scalaire vrai.
• Le produit scalaire de deux vecteurs vrais, qui sont donc tous les deux contravariants, leur norme variant en sens contraire des vecteurs de base, est doublement contravariant. Ce n'est donc pas à proprement parler un scalaire. L'énergie est une grandeur physique de ce type, puisqu'elle est définie comme produit scalaire d'une force et d'un déplacement, tous deux vecteurs vrais.

Norme

La norme d'un pseudovecteur est

• strictement scalaire si le pseudovecteur est du type (1,1) (1 fois contravariant, 1 fois covariant). Elle se calcule alors par la formule où a, b et c sont les coordonnées du pseudovecteur dans la base orthonormale choisie.
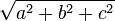
• un nombre doublement contravariant si le pseudovecteur est de type (2,0)
• un nombre doublement covariant si le pseudovecteur est du type (0,2).

Changement de base

Les pseudovecteurs obéissent à des formules de changement de base différentes de celle des vecteurs vrais.

Les bases des pseudovecteurs des trois types sont également différentes de la base duale (celle des covecteurs).

Les bases des pseudovecteurs sont différentes de celle des vecteurs vrais : en base orthonormée, cela se traduit par des changements de signe ; en base quelconque par des changements de toutes les coordonnées entre un vecteur et le pseudovecteur de même direction. Si on écrit pseudovecteurs et vecteurs vrais dans ce qui semble être une même base (i, j, k), il faudra de nouveau distinguer les bases lors d'opérations comme la symétrie plane. Et distinguer entre elles les bases des trois types de pseudovecteurs.

Produit mixte

Le produit mixte est défini par le déterminant

.

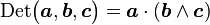
Si a est un pseudovecteur et b et c des vecteurs vrais, le résultat est un scalaire vrai. Dans les autres cas, il faut se référer à la définition du produit mixte.

Le produit mixte de trois vecteurs vrais est trois fois contravariant, comme les volumes. Il est cependant transformé en son opposé par une transformation qui transforme tous les axes en leurs opposés. Cette propriété n'est pas partagée par les volumes.

Torseurs

• La résultante d'un torseur est un vecteur vrai dans le cas d'un torseur cinétique, dynamique ou statique.
• La résultante d'un torseur est un pseudovecteur dans le cas d'un torseur cinématique.
• Le moment d'un torseur est un pseudovecteur dans le cas d'un torseur cinétique, dynamique ou statique.
• Le moment d'un torseur est un vecteur vrai dans le cas d'un torseur cinématique.

Rotationnel et Divergence

Rotationnel

Le rotationnel d'un champ de vrais vecteurs est un pseudovecteur. Ce pseudovecteur est du type 1 fois covariant, 1 fois contravariant.

En revanche, pour un champ de pseudovecteurs, il existe une contradiction entre deux approches.

• Si on garde les mêmes formules que pour les vecteurs (alors qu'on travaille dans une autre base!), le rotationnel est un vrai vecteur. C'est la définition la plus courante. L'exemple le plus connu est celui des équations de Maxwell : le rotationnel du pseudo vecteur champ magnétique B est proportionnel au vecteur courant, qui est un vecteur vrai :

.

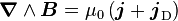
• En suivant la deuxième approche, les pseudovecteurs se comportant dans tous les cas comme des tenseurs du second ordre antisymétrique, on les analyse comme tels. Et alors on utilise la définition du rotationnel donnée pour les tenseurs du second ordre. Il apparaît alors quelque chose d'extraordinaire : le rotationnel d'un champ de pseudovecteurs calculé suivant cette définition a la même formule dans la base canonique des pseudovecteurs, que la divergence pour les champs de vecteurs vrais dans la base canonique des vecteurs vrais. C'est-à-dire que l'appellation usuelle de l'opérateur rotationnel pour les champs de pseudovecteurs est la divergence. Et celà est toujours nul.

Divergence

La divergence d'un champ de vrais vecteurs est un scalaire. En revanche, la divergence d'un champ de pseudovecteurs est toujours nulle. C'est la définition la plus courante, l'exemple usuel étant, à nouveau, le champ magnétique.

Synthèse

• Ce que l'on appelle communément rotationnel, a effectivement pour les vecteurs vrais la signification de rotationnel : les pseudovecteurs représente bien des rotations. Mais ceci a pour les pseudovecteurs la signication physique d'une divergence. Et pour les tenseurs du second ordre celle-ci est un vecteur.
• Ce que l'on appelle communément divergence est toujours nul pour les pseudovecteurs.