Réseau (géométrie) - Définition

Problèmes algorithmiques dans les réseaux

Un réseau formant un ensemble discret, il existe dans tout réseau un plus court vecteur non nul. Ce vecteur dépend bien évidemment de la norme dont on munit l'espace. Ce problème (souvent nommé SVP, de l'anglais Shortest Vector Problem) est connu pour être NP-difficile dans le cas de la norme euclidienne. Pour d'autres normes usuelles, rien n'est connu, mais on conjecture que le problème est au moins aussi difficile à résoudre.

Le problème non homogène associé est celui de trouver le vecteur d'un réseau le plus proche d'un vecteur donné dans . Il est souvent nommé CVP (de l'anglais Closest Vector Problem) et est lui aussi NP-difficile pour la norme euclidienne.

Certaines bases sont mieux adaptées que d'autres pour travailler dans un réseau car elles sont formées de vecteurs courts et permettent donc de se promener localement aux alentours d'un point donné du réseau. On les appelle bases réduites et ces méthodes, réductions de réseau. Il existe plusieurs notions différentes de réductions mais la réduction LLL inventée par Lenstra, Lenstra et Lovász présente l'avantage d'être calculable en temps polynomial par l'algorithme LLL. Cet algorithme qui fournit une base de vecteurs assez courts a de multiples applications, notamment en cryptographie à clé publique.

Usages

Volume fondamental

En théorie des nombres, si α est un entier algébrique, sa norme au sens arithmétique, est égal au déterminant de l'application qui à un entier algébrique β associe α.β. Un rapide calcul montre que la norme d'un entier de Gauss a + i.b est égale à a² + b². Si la base (1, i) est identifiée avec la base canonique de R², la valeur absolue de la norme (toujours positive dans l'exemple des entiers de Gauss, mais parfois négative dans d'autres anneaux d'entiers algébriques) s'interprète comme le volume fondamental du réseau. Dans le premier exemple choisi, la norme de 2 + i est égale à 5, le nombre d'entiers de Gauss qui se trouvent dans le domaine fondamental. Ce résultat s'interprète comme le fait que la norme d'un entier algébrique est égal au cardinal de l'anneau quotienté par l'idéal principal engendré par l'entier. Cette propriété est toujours vraie et se démontre à l'aide de considérations géométriques sur un réseau.

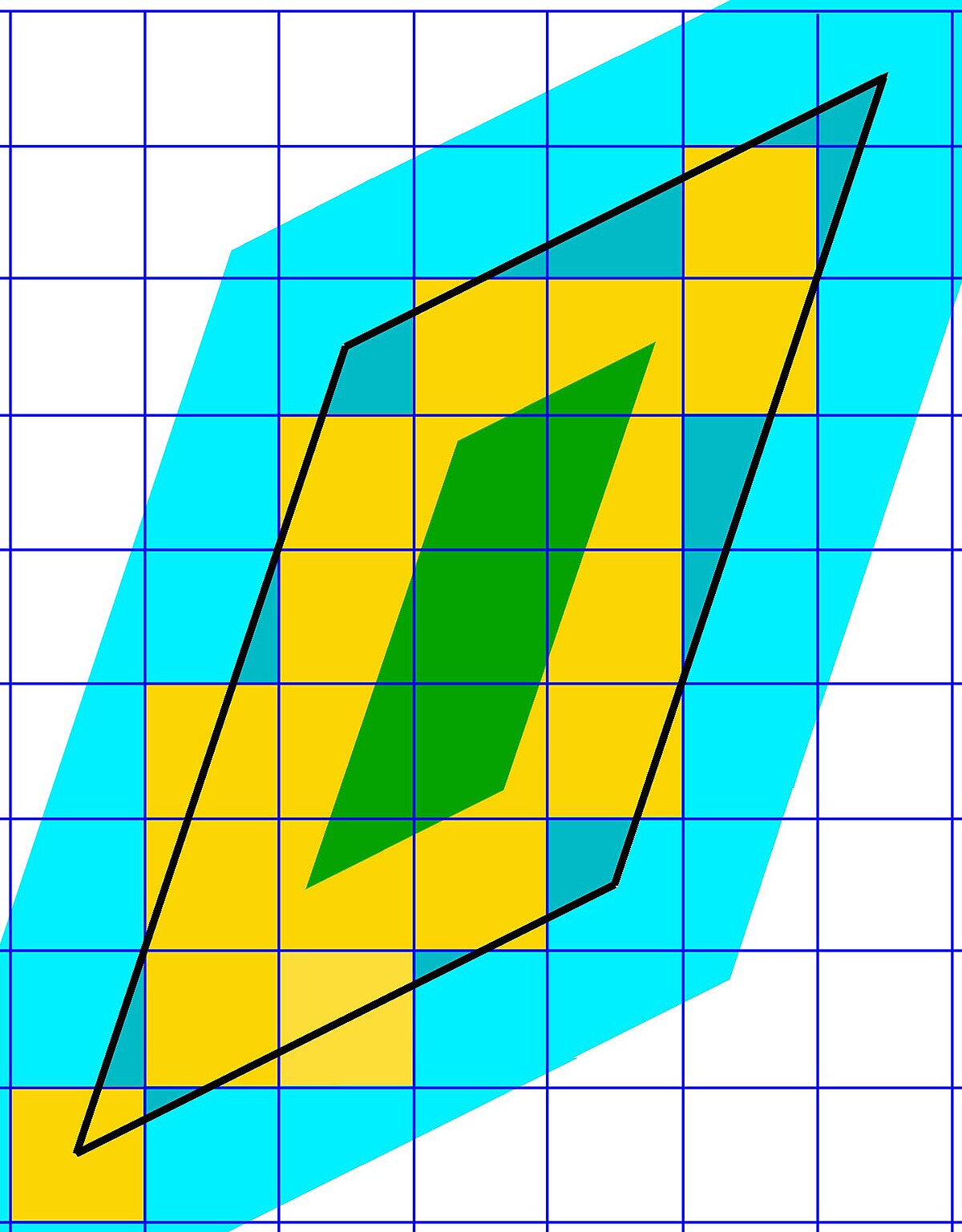
La figure de gauche illustre un domaine fondamental associé à un entier algébrique. Le domaine fondamental correspond à la zone à l'intérieur de la frontière dessinée en noir. À chaque point de l'anneau à l'intérieur du domaine fondamental, est dessiné un carré jaune de centre le point de l'anneau et de côté de longueur 1. L'objectif est de montrer que la mesure de la surface réunion des différents petits carrés est la même que le volume fondamental. Si l'on éloigne les frontières de 1, on obtient la forme en bleu clair, qui contient nécessairement la surface jaune. Si l'on approche les frontières de 1, on obtient la forme en vert, qui est nécessairement incluse dans la surface jaune, d'où l'existence d'un encadrement.

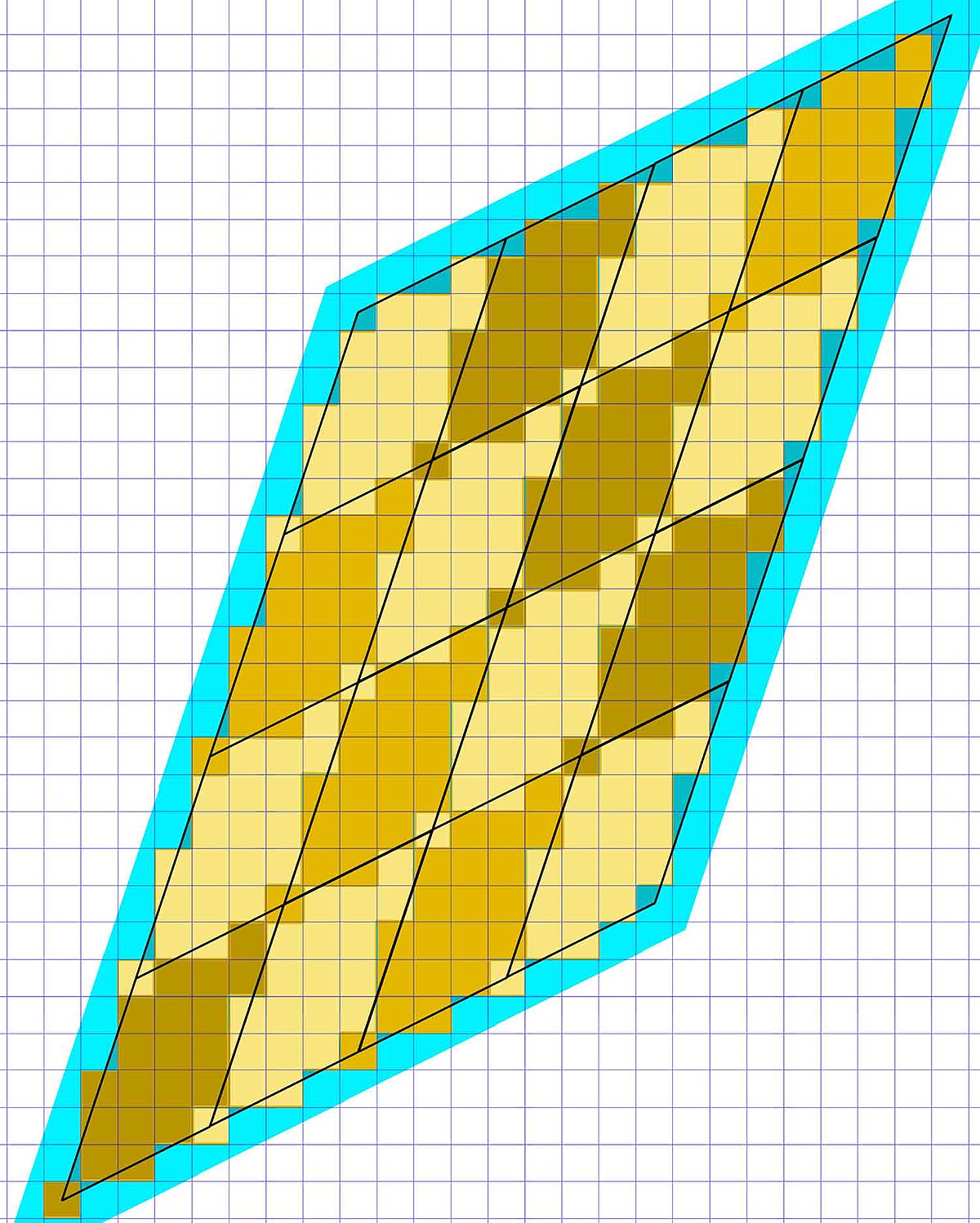
Illustré à droite, on réalise la même opération, mais cette fois sur n² translatés de volumes fondamentaux. Les petits carrés jaunes, qui représentent tous les points de l'anneau à l'intérieur du grand parallélogramme, forment une partition du parallélogramme, à la précision de la frontière près. L'incertitude relative dû aux phénomènes de frontières devient plus réduite. Si n est choisi suffisamment grand, on obtient l'égalité entre les deux surfaces.

Ce résultat est à rapprocher du théorème de Pick qui indique, en dimension 2 la relation entre le nombre de points du réseau contenu dans un polytope P dont les sommets sont des éléments du réseau et la surface du polytope. La généralisation en dimension n est obtenue à l'aide du polynôme d'Ehrhart.

Ensemble convexe

Exemple de convexe traité par le théorème de Minkowski.

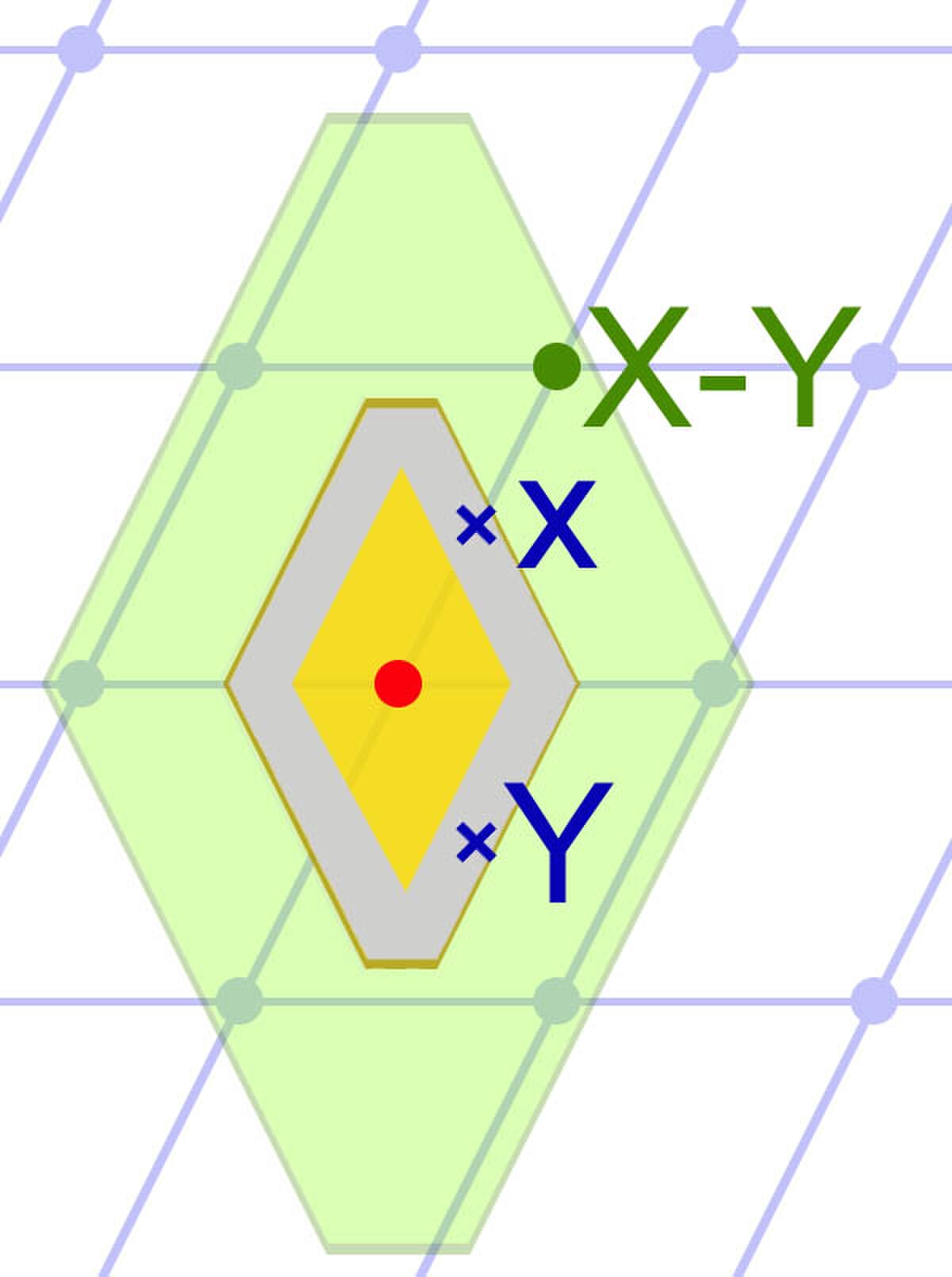
Le théorème de Minkowski indique qu'un convexe symétrique par rapport à l'origine et de volume supérieur à 2ⁿ.V de Rⁿ rencontre nécessairement un point non nul du réseau si V est son volume fondamental. La figure de droite représente un convexe symétrique par rapport à l'origine, son volume est donc inférieur à 8 fois le volume fondamental, car il ne rencontre le réseau qu'au point d'origine.

Une démonstration élégante utilise la représentation du volume fondamental sous forme de tore. Supposons que le convexe C, illustré en vert sur la figure de gauche, soit de volume supérieur à 2ⁿ.V, l'image du convexe par une homothétie de rapport 1/2 est de volume supérieur à celui du tore. Cette configuration est illustré sur la figure de gauche. La restriction du morphisme canonique de Rⁿ dans Rⁿ/Λ ne peut être injective, car sinon Rⁿ/Λ contiendrait un volume dont la mesure serait strictement supérieure à la sienne. Il existe donc deux points x et y ayant même image par le morphisme, où encore x - y est élément de Λ. Or x et -y sont éléments de 1/2 C et 1/2(x - y) l'est aussi, donc x - y est élément de C. La zone où le morphisme n'est pas bijectif est indiqué en gris sur la figure de droite. Son image par le morphisme est la zone grise du tore illustré dans le paragraphe sur le Volume fondamental. L'article détaillé propose aussi une autre démonstration, légèrement plus calculatoire, mais utilisant des outils plus simples.

Cette technique est utilisée par exemple pour établir le théorème des unités de Dirichlet, élucidant la structure du groupe des unités d'un anneau d'entiers algébriques.