Réseau (géométrie) - Définition

Introduction

En mathématiques, un réseau d'un espace euclidien est un maillage correspondant à la figure de droite. Il remplit l'espace au sens ou il existe un rayon R tel que toute boule de rayon R contient au moins un point du réseau. Il est discret au sens ou il existe un nombre strictement positif r tel que toute boule de rayon r contient au plus un point du réseau. Il est régulier au sens où la somme et la différence de deux points du réseau est encore élément du réseau.

L'étude des réseaux est à la croisée de différentes branches des mathématiques. Pour un théoricien des groupes, un réseau est avant tout un cas particulier de groupe commutatif qu'il appelle groupe abélien libre de type fini. Pour un algébriste, un réseau ressemble à un espace vectoriel de dimension finie, à la différence que les scalaires non nuls, c'est-à-dire les nombres qui multiplient les vecteurs, n'ont pas toujours d'inverse. Si les visions précédentes apportent informations et théorèmes sur la structure d'un réseau, elles ne correspondent ni à l'origine du terme ni aux méthodes mathématiques spécifiques aux réseaux. Ce terme réseau provient initialement d'une la question de nature physique, l'étude des cristaux. Dans cette branche du savoir un réseau porte le nom de réseau de Bravais et les outils d'analyse sont essentiellement géométriques. Les questions propres à l'analyse d'un réseau portent sur les différentes symétries qui laissent invariant le réseau ou encore la résolution de problèmes d'empaquements de sphères ou de convexes. Cette approche offre des démonstrations parfois plus simples de théorèmes déjà connus et parfois nouvelles, bien difficiles à démontrer sans l'apport de la géométrie.

Si une subdivision en différentes branches des mathématiques est utile, la définition des frontières est nécessairement floue. Un théoricien des groupes, ou un algébriste, utilise avec bonheur des outils géométriques pour parvenir à ses fins. Ainsi, l'usage d'un réseau se trouve dans de nombreux pans des mathématiques. En théorie des groupes, on le retrouve pour l'étude des groupes de Lie et de leurs algèbres, il est aussi présent pour l'étude des représentations d'un groupe fini. En arithmétique, il est l'outil de base d'une branche entière appelée géométrie arithmétique. La physique en fait usage pour étudier la répartition des atomes ou des ions dans un solide cristallin. Le réseau est source d'algorithmes en usage en informatique. Il est à la base de méthodes pour casser des codes secrets ou encore pour en construire d'autres, probablement difficilement violable. Le terme difficile possède ici une définition aussi précise que particulière. Il ne signifie pas que personne ne sait comment déchiffrer le message codé, mais seulement qu'il n'existe pas de méthode qui permette de le faire en un temps raisonnable, par exemple inférieur à l'âge de l'univers.

Algèbre linéaire et espace métrique

Dans cet article les lettres , , et désignent respectivement le corps des imaginaires encore appelés complexes, des nombres réels, des rationnels et l'anneau des nombres entiers et n un entier strictement positif. L'espace vectoriel désigne l'ensemble des n-uplets composés de n nombres réels dans un ordre donné. Géométriquement, on les imagine comme les coordonnées d'un point dans un espace muni d'un repère orthonormal. En dimension 2 ou 3, on obtient une représentation du monde physique, à la condition qu'il soit approximé par une géométrie euclidienne.

Définition

L'hexagone est une figure permettant de construire un réseau en dimension 2.

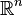
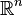
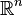
Une telle définition mérite quelques explications. Le choix de au lieu d'un espace vectoriel réel de dimension n n'est que de peu d'importance. Tout espace vectoriel réel de dimension n est une copie de et les résultats vrais dans le sont dans un espace réel de dimension n. On parle d'isomorphisme. Le fait que les points forment un groupe implique la régularité du réseau. Un polygone de sommets des points du réseau, translaté par un déplacement d'un point du réseau à un autre, possède toujours pour sommets des points du réseau. L'exemple de droite l'illustre. Les points du réseau correspondent à l'intersection du quadrillage, l'hexagone en violet, translaté possède toujours des sommets éléments du réseau. Le terme de discret possède la signification suivante :

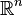
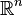
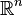
• Un sous-ensemble V d'un espace métrique est dit discret lorsque l'intersection de cet ensemble avec une boule de rayon fini contient un nombre fini d'éléments.

Un espace métrique (M,d) est simplement un ensemble M munis d'une distance d, et une boule de rayon r, B(a,r) où r et un entier positif, généralise la notion de disque. Elle correspond à l'ensemble des points qui sont à une distance inférieure à r d'un point a donné :

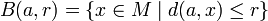
La stabilité par translation montre que pour vérifier qu'un groupe est discret, il suffit de considérer les boules de centre l'élément neutre. Si chacune de ces boules, de rayons finis, ne contient qu'un nombre fini de points du réseau, alors le groupe est discret. Il existe certains groupes qui ne le sont pas. Par exemple , celui formé par les points dont les coordonnées, dans la base canonique de , sont les nombres rationnels.

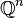
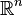
La troisième propriété signifie qu'il n'existe pas de sous-espace vectoriel strict contenant le réseau. Si la dimension est égale à 3, alors aucun plan ne contient le réseau. Si un plan entier est couvert et s'il existe un unique point du réseau en dehors d'un plan, la stabilité de l'addition et de la soustraction montre que l'espace entier est couvert. Dire que l'espace est couvert signifie qu'il existe un rayon ρ tel que toute boule de rayon supérieur à ρ contient au moins un point du réseau, et ceci quel que soit son centre.

Tout espace vectoriel E de dimension n sur les nombres complexes est aussi un espace vectoriel réel de dimension 2.n. Ainsi, si Λ est un groupe discret qui génère E, en tant qu'espace vectoriel réel, il est un réseau de dimension 2.n. De même que est un réseau de , Gⁿ est un réseau de . La lettre G désigne ici les entiers de Gauss, c'est-à-dire les nombres de la forme a + i.b où a et b sont des éléments de .

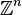
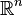
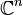
Base

Dans un réseau, il existe une famille, illustré en rouge sur la figure, tel que tout point s'exprime comme combinaison linéaire de manière unique, des points de la famille.

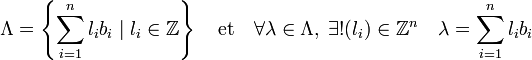
Il existe plusieurs manières de lire et de démontrer ce théorème. En termes de théorie des groupes, un réseau est un groupe abélien de type fini, c'est-à-dire qu'il est commutatif et que de plus, il existe une famille finie (f_i), génératrice du groupe. C'est-à-dire que tout élément g du groupe est somme des éléments g_i.f_i si g_i sont des entiers bien choisis. Le terme g_i.f_i signifie, si g_i est positif, la somme de f_i avec lui-même, répétée g_i fois et son inverse si g_i est négatif. Un tel groupe est dit sans torsion, si, quand on additionne avec lui-même un élément non nul du groupe, autant de fois qu'on le désire, on n'obtient jamais le point origine. On parle alors de groupe abélien libre de type fini et l'on montre avec ces hypothèses l'équivalent de l'existence d'une base.

Une autre manière de voir les choses est de faire usage de l'algèbre linéaire. On considère le réseau comme un quasi espace vectoriel, à la différence que les scalaires ne sont pas tous inversibles. Les scalaires ici sont égaux aux nombres entiers. Une telle structure porte le nom de module. S'il existe une famille génératrice finie, si le Z-module forme un groupe additif sans torsion, le théorème des facteurs invariants est une manière de montrer le résultat.

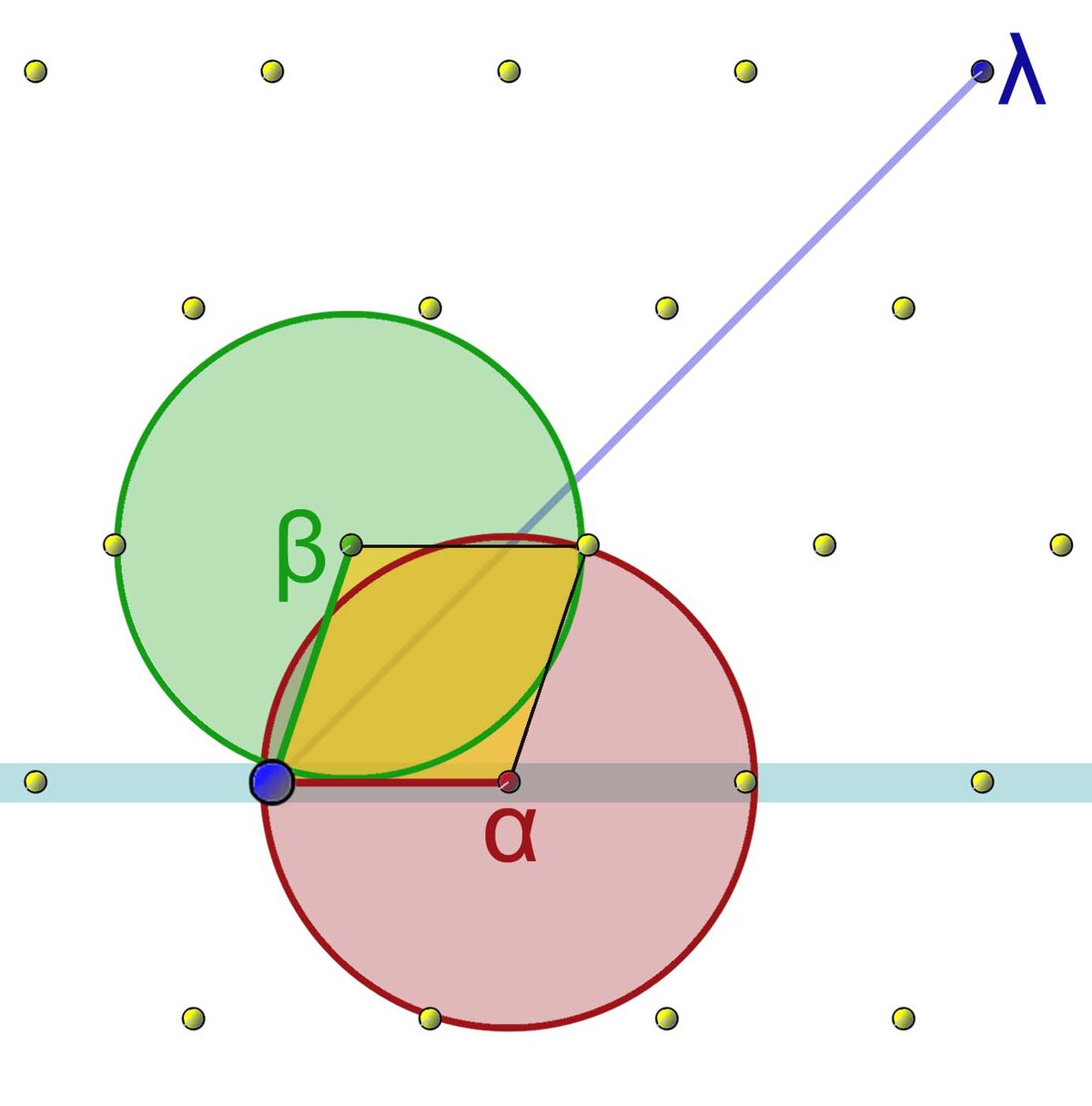
Ces démonstrations sont bien peu géométriques et n'utilisent guère les outils associés aux réseaux. On peut imaginer une démonstration directe, guidé par l'intuition géométrique qu'apporte une telle structure. Le principe est illustré en dimension 2 sur la figure de gauche. On considère deux vecteurs libres du réseau, choisis de norme la plus petite possible. La norme est le terme mathématique technique désignant la longueur d'un vecteur. On appelle ces vecteurs α et β. Ils définissent un parallélogramme, en jaune sur la figure. La minimalité des normes de α et β permet de montrer que ce parallélogramme ne contient aucun point du réseau autre que ses sommets.

On considère, un point λ quelconque du réseau, que l'on peut toujours exprimer comme une combinaison linéaire de α et β si la structure considérée est l'espace vectoriel R². En retranchant à λ le vecteur de coordonnées les parties entières de celle de λ on obtient un petit vecteur du réseau, à l'intérieur du parallélogramme jaune. Ce principe est un peu analogue à une division euclidienne. Le petit vecteur serait, avec cette analogie, le reste. Le fait qu'il soit dans le parallélogramme et dans le réseau, montre qu'il est nul. Le vecteur λ s'exprime donc comme une combinaison linéaire de α et β avec des coefficients entiers.

Cette démonstration, ainsi que sa généralisation en dimension quelconque est plutôt plus simple que les deux citées précédemment. L'usage de la géométrie simplifie l'approche. En revanche, la méthode proposée ici n'est pas effective, à la différence de celle des facteurs invariant, par exemple. Effective signifie que l'on peut, avec cette méthode, construire effectivement une base. Dans le cas général, il est difficile de trouver le vecteur non nul de plus petite norme.

• Dimension 2 :

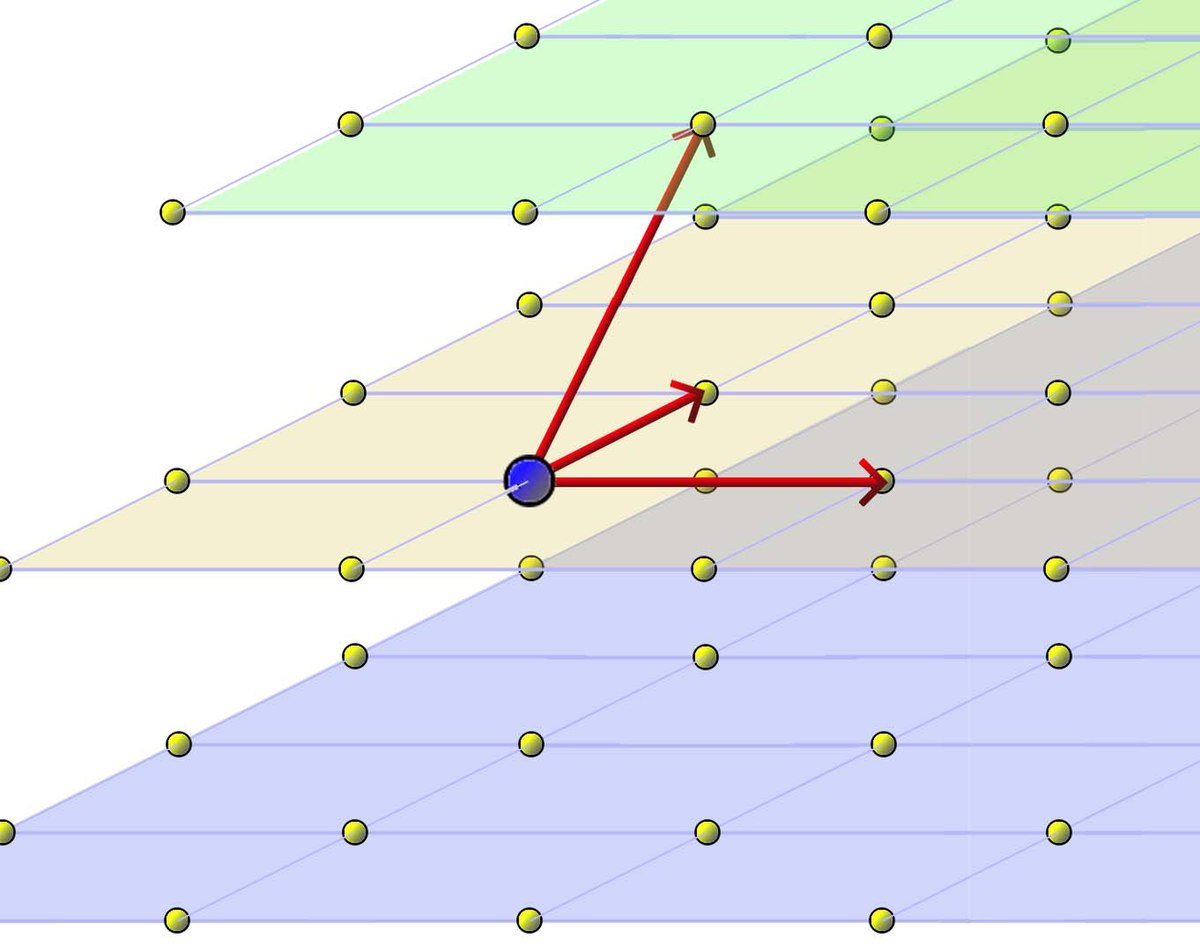
Le réseau n'est pas limité au vecteur nul, car il engendre l'espace vectoriel R², il existe au moins un vecteur de norme non nul, soit b cette norme. Le disque de centre le vecteur nul et de rayon b intersecte le réseau en un autre point que l'origine et contient un nombre fini du points du réseau. Ce qui montre qu'il existe au moins un vecteur α non nul de plus petite norme dans le réseau. On considère maintenant le réseau ôté des multiples de α. L'ensemble est non vide car sinon le réseau n'engendrerait pas l'espace vectoriel R², le même raisonnement que le précédent montre l'existence d'un vecteur β de longueur minimale, dans le réseau, à l'exception peut-être de quelques multiples de α, correspondant à la bande bleue sur la figure de gauche. Le gros point bleu est l'origine. Le vecteur α est bien un vecteur non nul de plus petite norme du réseau et vient ensuite β, dont la norme n'est minorée que par celle de α, son inverse et le vecteur nul.

Il n'existe au plus qu'une manière d'écrire un vecteur du réseau comme combinaison linéaire de α et β. En effet, cette propriété est une conséquence du fait que ces deux vecteurs sont libres dans l'espace vectoriel R². Il n'existe qu'une unique manière d'écrire un vecteur quelconque de R² comme combinaison linéaire α et β, ce qui est en particulier vrai pour les vecteurs du réseau.

Montrons maintenant que tout vecteur du réseau est combinaison linéaire de α et β, à coefficients entiers. Considérons le disque rouge, de centre α et de rayon la norme de β, un tel disque ne peut contenir comme point du réseau, en dehors de sa frontière, que quelques multiples de α dans la zone bleue sur la figure, d'après la définition de la norme de β. Le disque vert est de centre β et de rayon la norme de α. Le même raisonnement montre que l'intérieur de ce disque ne peut contenir aucun point du réseau. Le segment [0, α] ne peut contenir que ses extrémités comme point du réseau, il en est de même pour le segment [0, β]. Il en est aussi de même pour [α, + β] et [β, α + β] car sinon, en soustrayant α ou β, on aurait une contradiction. En résumé, le parallélogramme, en jaune, de sommets 0, α, β et α + β ne contient aucun autre point du réseau que ses sommets. On remarque que ce parallélogramme est constitué des vecteurs de R² ayant deux coefficients compris entre 0 et 1 dans la base (α, β).

Considérons un élément quelconque λ du réseau. Il est nécessairement combinaison linéaire de la base (α, β) de R², et λ = a.α + b.β avec a et b élément de R. L'objectif est de montrer que a et b sont des nombres entiers. Soit p_a (resp. p_b) la partie entière de a (resp. b) et r_a (resp. r_b) sa partie fractionnaire. Comme α et β sont des éléments du réseau et que p_a et p_b sont des nombres entiers, p_a.α + p_b.β est un point du réseau au même titre que λ. Leur différence, égale à r_a.α + r_b.β est donc dans le réseau. C'est aussi un point du parallélogramme jaune car ses deux coordonnées sont comprises entre 0 et 1. Il existe quatre points du réseau possible, comme une partie fractionnaire est toujours strictement plus petite que 1, la seule valeur possible est 0, ce qui montre que a est égal à p_a et b à p_b. Autrement dit, les coordonnées de λ dans la base sont entières, ce qui termine la démonstration.

• Dimension quelconque :

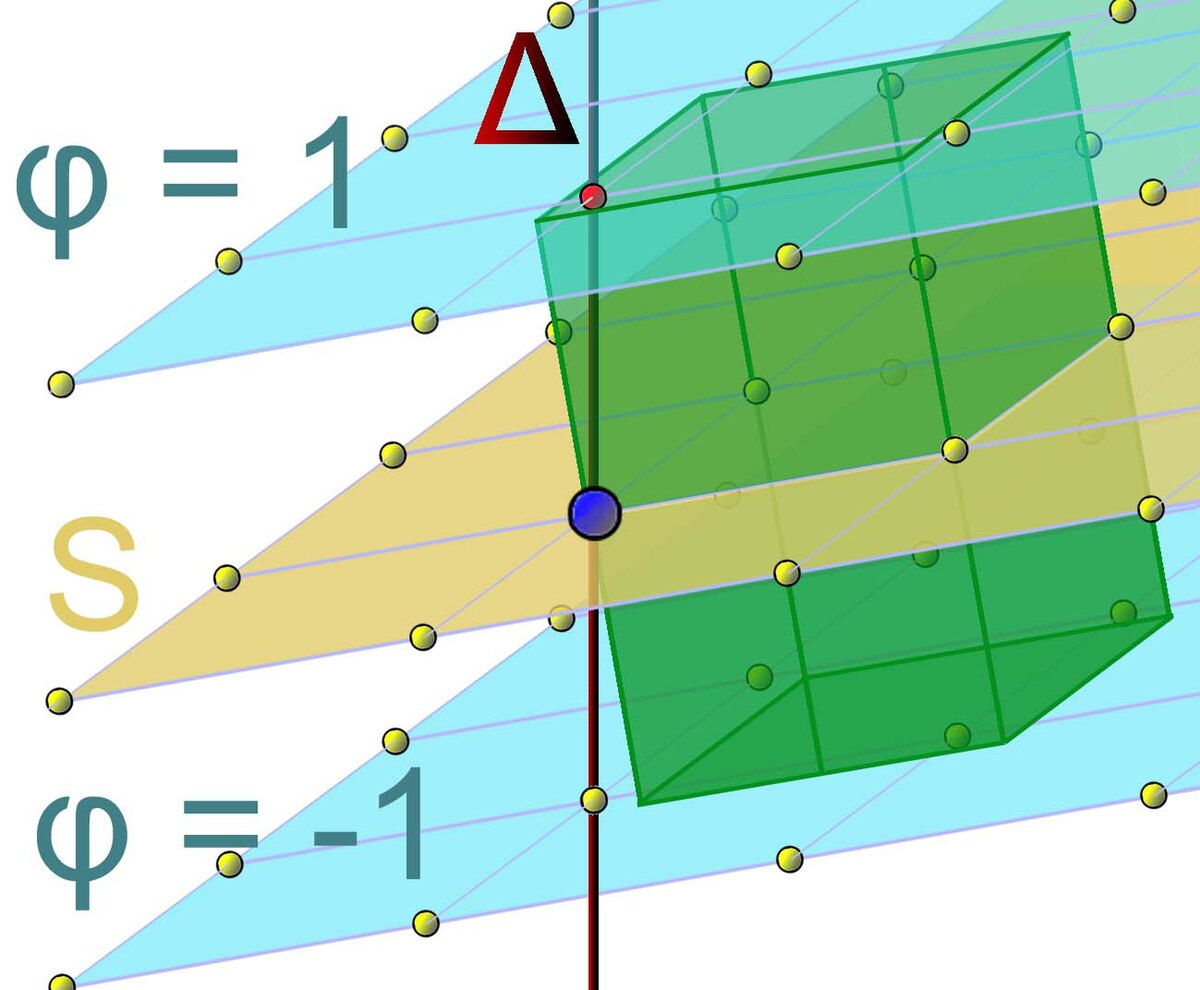
Démontrons ce résultat par récurrence sur n. Pour les dimensions 1 et 2, une démonstration est déjà présentée. Supposons la propriété démontrée à l'ordre n - 1 et démontrons là à l'ordre n. Le réseau forme une famille génératrice de Rⁿ, de toute famille génératrice, il est possible d'extraire une base, il existe donc une sous-famille du réseau de cardinal n qui engendre l'espace entier. Soit (f_i), pour i variant de 1 à n, une telle base. Elle n'est pas a priori celle recherchée car rien n'indique que les éléments du réseau s'expriment comme combinaison linéaire à coefficients entiers dans cette base. Soit S l'espace vectoriel engendré par (f_i), pour i variant de 1 à n - 1. L'intersection du réseau et de S est un groupe discret engendrant S, il existe une base (b_i), pour i variant de 1 à n - 1 de l'intersection du réseau et de S, par hypothèse de récurrence. L'hyperplan S est représenté sur la figure de droite, couleur crème, le vecteur nul est le point bleu. La famille (b_i) est un bon candidat pour la base recherchée, mais il manque encore un vecteur.

Soit φ une forme linéaire nulle sur S tel que l'image du réseau par φ ne soit pas réduite à 0. Une telle forme existe, sinon le réseau n'engendrerait que l'espace S et pas l'espace entier. L'objectif est de montrer que l'image par φ du réseau est un sous-groupe discret de R, c'est-à-dire qu'il existe un réel strictement positif ε tel que si u est un élément du réseau, l'image du réseau par φ ne contient que la valeur φ(u) entre φ(u) - ε et φ(u) + ε. On remarque que l'on peut supposer u nul, en effet, si l'image par φ du réseau n'est pas discret, quel que soit ε, il existe deux vecteurs u et v d'images distinctes par φ et dont la différence est, en valeur absolue inférieur à ε, ce qui montre que l'image par φ de u - v est, en valeur absolue, inférieure à ε.

Pour montrer ce résultat, on va montrer qu'il n'existe qu'un nombre fini de valeurs atteintes par φ sur l'intervalle [-1, 1]. Tous les points du réseau ayant une image par φ dans cet intervalle se trouvent entre les hyperplans affines d'équation φ(x) = - 1 et φ(x) = 1, représentés en bleu sur la figure. Soit V le volume de Rⁿ composé des vecteurs compris entre les deux hyperplans et dont les coordonnées, dans la base (b_i), de la projection orthogonale par p sur S, sont toutes comprises entre 0 et 1. Le volume V est représenté en vert sur la figure. On remarque que V est bien borné car il représente l'ensemble des vecteurs de Rⁿ ayant des coordonnées comprises entre 0 et 1 dans la base (b_i, ,π). Ici π désigne le vecteur orthogonal à S et d'image égale à 1 par la forme φ. Si δ est un nombre réel, compris entre -1 et 1, et image du réseau par φ, δ possède un antécédent dans V. En effet, il existe un vecteur u du réseau compris entre les deux hyperplans et tel que φ(u) = δ. Le vecteur p(u) est dans S et se décompose sur la base (b_i), soit (u_i) les coordonnées de p(u) dans cette base. Si q_i désigne la partie entière de u_i et r_i la partie fractionnaire :

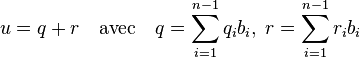
On remarque que q est un élément du réseau car combinaison linéaire de la famille (b_i) à coefficients dans Z. Son image par φ est nulle car il est élément de S. Le point u - q est constitué de la différence de deux éléments du réseau et fait partie du réseau. L'image de q par φ est nulle et φ est linéaire. La projection orthogonale de u - q sur l'hyperplan engendré par S est égal à r, ce qui montre que u - q est bien un élément de V. Le volume V est borné, il ne contient qu'un nombre fini de points du réseau, car le réseau est discret. Il ne peut exister qu'un nombre fini de valeurs prises par l'image du réseau par la fonction φ entre -1 et 1, ce qui montre que la valeur 0 est bien isolée dans cette image.

Soit Δ une droite vectoriel de Rⁿ non contenu dans S et contenant un point non nul du réseau. L'image par φ de Δ est un groupe discret d'après la démonstration précédente, il existe un point b_n de Δ et du réseau de plus petite image a strictement positive par φ, ce point est représenté en rouge sur la figure. Soit enfin un élément λ quelconque du réseau, l'élément λ s'exprime comme une combinaison linéaire de (b_i), car cette famille est une base de Rⁿ. Il faut alors montrer que les différents coefficients sont des entiers :

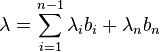
L'image par φ de λ est égal à λ_n.a, qui est un élément de a.R, l'image de Δ par φ. On en déduit que λ_n est entier. Le vecteur λ- λ_nb_n est élément du réseau et de S, ce qui montre que les coordonnées λ_i sont toutes entières. La famille (b_i), pour i variant de 1 à n de Rⁿ est génératrice du réseau. Le fait qu'elle soit de cardinal n termine la démonstration.

 

Domaine fondamental

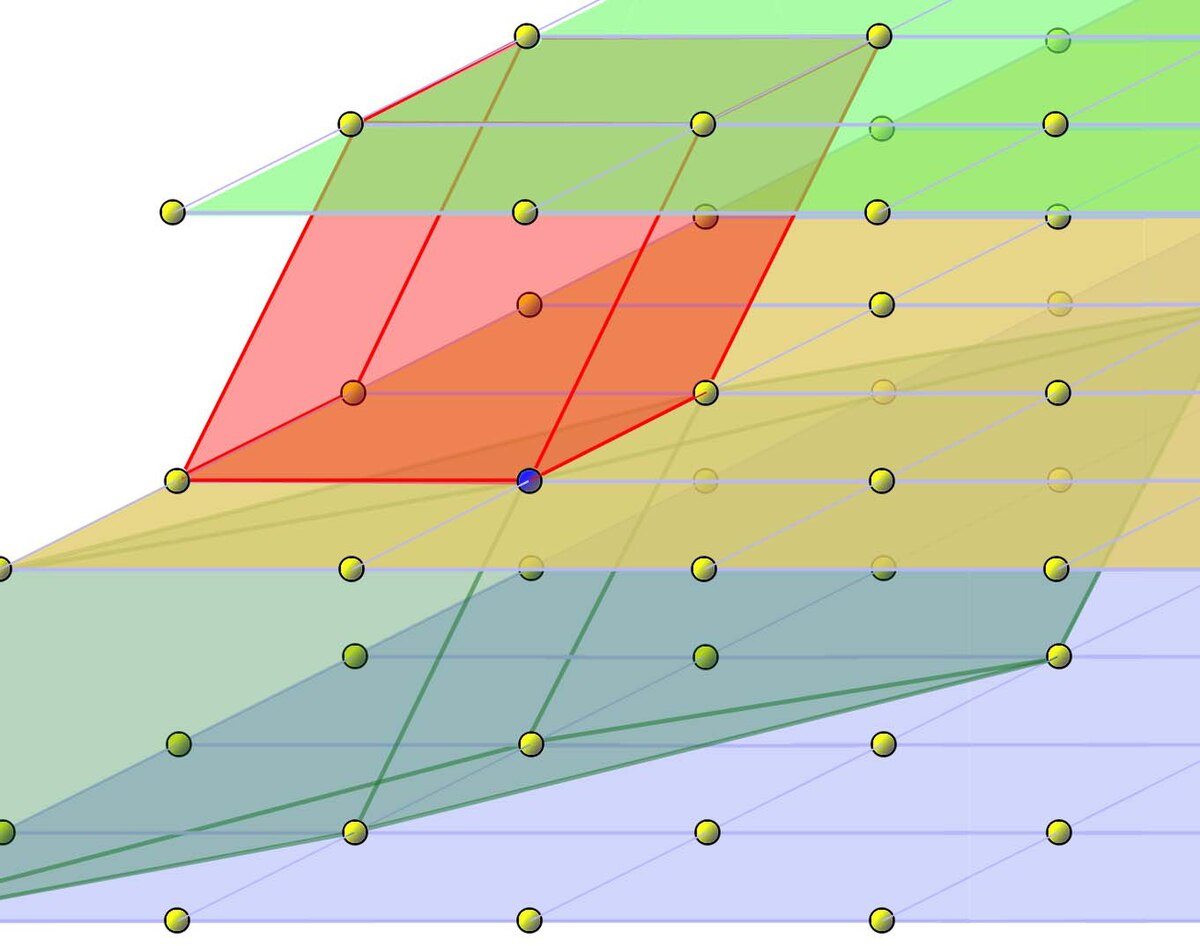
Une zone particulière a été utilisé, dans la démonstration précédente, elle correspond à la zone illustrée en jaune pour la dimension 2. Elle correspond à la définition suivante :

Définition d'un domaine fondamental — 

• Le domaine fondamental par rapport à une base B , si B est une base (b_i) du réseau est l'ensemble des points P :

Deux domaines fondamentaux ont même volume.

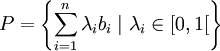
La zone rouge de la figure de droite est un exemple de volume fondamental. La définition d'un domaine fondamental s'obtient à partir d'une base. Pour les réseaux, comme pour les espaces vectoriels, il existe plusieurs bases et, en conséquence plusieurs volume fondamentaux. À part en dimension 1, où il n'en existe que deux, ayant la même géométrie, il en existe dans tous les autres cas une infinité. Pour s'en rendre compte il suffit de remplacer le deuxième vecteur de la base par la somme de k fois le premier vecteur et le deuxième. Si k désigne un entier, on a là un moyen de construire une infinité de bases aux géométries différentes. Sur la figure de droite, la zone verte est un autre domaine fondamental.

Il existe un invariant associé au domaine fondamental. Le volume fondamental d'un réseau est la mesure du volume du domaine fondamental et lui est unique. Sur la figure de droite, les volumes définis par les parallélépipèdes vert et rouge sont égaux.

Il existe une manière intrinsèque de définir le domaine fondamental, elle fait appel à des concepts plus avancés. Le groupe de Lie Rⁿ / Λ dispose d'une mesure canonique. Pour tout point p de Rⁿ / Λ, il existe un ouvert de p tel que la projection canonique de Rⁿ dans Rⁿ / Λ soit un difféomorphisme. Ces difféomorphismes permettent de définir une mesure. Le groupe de Lie est compact, sa mesure totale peut être choisie égale au volume fondamental du réseau.

Une manière simple de voir les choses est de se limiter en dimension 2. Les points de première coordonnée égal à un entier sont identifiés avec les points de première coordonnée égal à 0. Cela revient à enrouler l'espace pour obtenir un cylindre où tous les points de première coordonnée entière sont superposés. On identifie alors les points de deuxième coordonnée égal à un entier aux points de deuxième coordonnée égal à 0. Cela revient à enrouler le cylindre pour obtenir un tore, illustré sur la figure de gauche.

La représentation est, en termes de mesure imparfaite. Les cercles horizontaux du tore correspondent aux points de deuxième coordonnée constante. Tous ces cercles ont une circonférence égale à 1. Dans la représentation, selon que le cercle est plus ou moins choisi à l'intérieur du tore, la circonférence varie. À ce détail près, la représentation par une forme s'approchant d'une bouée est un bon support pour l'intuition de la géométrie du volume fondamental d'un réseau.