Sécurité des réacteurs chimiques - Définition

Introduction

La réaction chimique, en vertu des énergies considérables qu'elle implique, peut mener, si elle est conduite de manière non contrôlée, à des accidents extrêmement graves, comme des explosions, qui peuvent être mortelles. Parmi les cas les plus marquants, citons le cas de la catastrophe de Seveso, où une pollution majeure à la dioxine fut provoquée par l'emballement d'un réacteur. En raison de tels accidents survenus par le passé, le public perçoit bien souvent l'industrie chimique comme une menace importante pour son environnement. La sécurité des procédés chimiques, et en particulier celle des réacteurs est de nos jours une préoccupation majeure de cette industrie.

De manière générale, l'accident survient lorsque la chaleur produite par la réaction chimique ne peut plus être intégralement évacuée par le système de refroidissement, ce qui provoque une accumulation d'énergie, sous forme d'augmentation de température et de pression, qui peut mener à l'explosion.

Une évaluation du danger est nécessaire pour chaque étape du procédé, de l'arrivée des réactifs jusqu'au transport des produits, en passant par leur conditionnement. Certains accidents majeurs ont par exemple été provoqués par des stockages mal dimensionnées ou défectueux, comme la catastrophe de Bhopal ou celle de l'usine AZF à Toulouse. Les concepts développés ci-dessous concernent essentiellement la sécurité des réacteurs, mais ils sont cependant largement applicables aux sites de stockages.

Effet de la taille sur la sécurité des réactions chimiques

Les problèmes de sécurité liés à l'énergie libérée par les réactions chimiques ne surviennent pas forcément au laboratoire, mais apparaissent plus tard lors du passage à l'échelle industrielle.

Le changement du rapport surface sur volume explique cet état de fait. L'énergie libérée par une réaction est proportionnelle à la quantité de réactif, ou en d'autre termes, celui de la masse réactionnelle. L'évacuation de la chaleur dégagée par la réaction passe par la surface d'échange (manteau du réacteur, paroi du silo, etc.). Comme le volume augmente au cube de la taille caractéristique, alors que la surface augmente seulement avec le carré, le rapport surface sur volume diminue proportionnellement à la taille.

Ainsi si l'on multiplie l'arête d'un cube par 10, on multiplie son volume par 1000 et sa surface par 100, et donc son rapport sur surface sur volume diminue d'un facteur 10. Ainsi s'il est relativement facile d'évacuer la chaleur produite dans un petit volume, il est bien plus difficile de refroidir un réacteur de taille industrielle.

Diagramme de Semenov

Lors du développement d'un procédé chimique, on procède systématiquement à une étude de risque. Lors de celle-ci, on va notamment chercher à déterminer si le réacteur peut s'emballer, et chercher à déterminer le point à partir duquel l'emballement survient, appelé point de non-retour.

En premier lieu, lors de l'étude de risque, on va faire les approximations que la réaction étudiée a une cinétique d'ordre zéro, et que seul le manteau caloporteur du réacteur peut évacuer la chaleur. Ces deux approximations sont péjorantes : elles ne font qu'aggraver le risque. En effet, si la réaction a une cinétique d'ordre supérieure à zéro, la réaction va ralentir au fur et à mesure que le réactif s'épuise, et la puissance développée par la réaction va ainsi diminuer.

Le bilan de chaleur pour un tel système s'écrit :

Qui se simplifie en :

Le terme « Sortie » fait référence à l'évacuation de chaleur par le manteau du réacteur, soit :

Où T_r et T_c représentent la température respectivement au sein du réacteur et dans le manteau de refroidissement. UA est le coefficient global de transfert thermique, avec comme unité .

La puissance libérée par la réaction est donnée par :

Où − ΔH_R est l'enthalpie de réaction, qui est négative pour une réaction exothermique. En introduisant la loi d'Arrhenius, qui donne l'accélération de la vitesse de réaction en fonction de la température, on obtient (avec l'approximation que la cinétique est d'ordre zéro) :

Où k₀ est le facteur de fréquence, C₀ la concentration initiale du réactif limitant, R la constante des gaz parfaits, et E_a l'énergie d'activation.

On arrive donc à l'expression suivante pour l'accumulation de chaleur dans le réacteur :

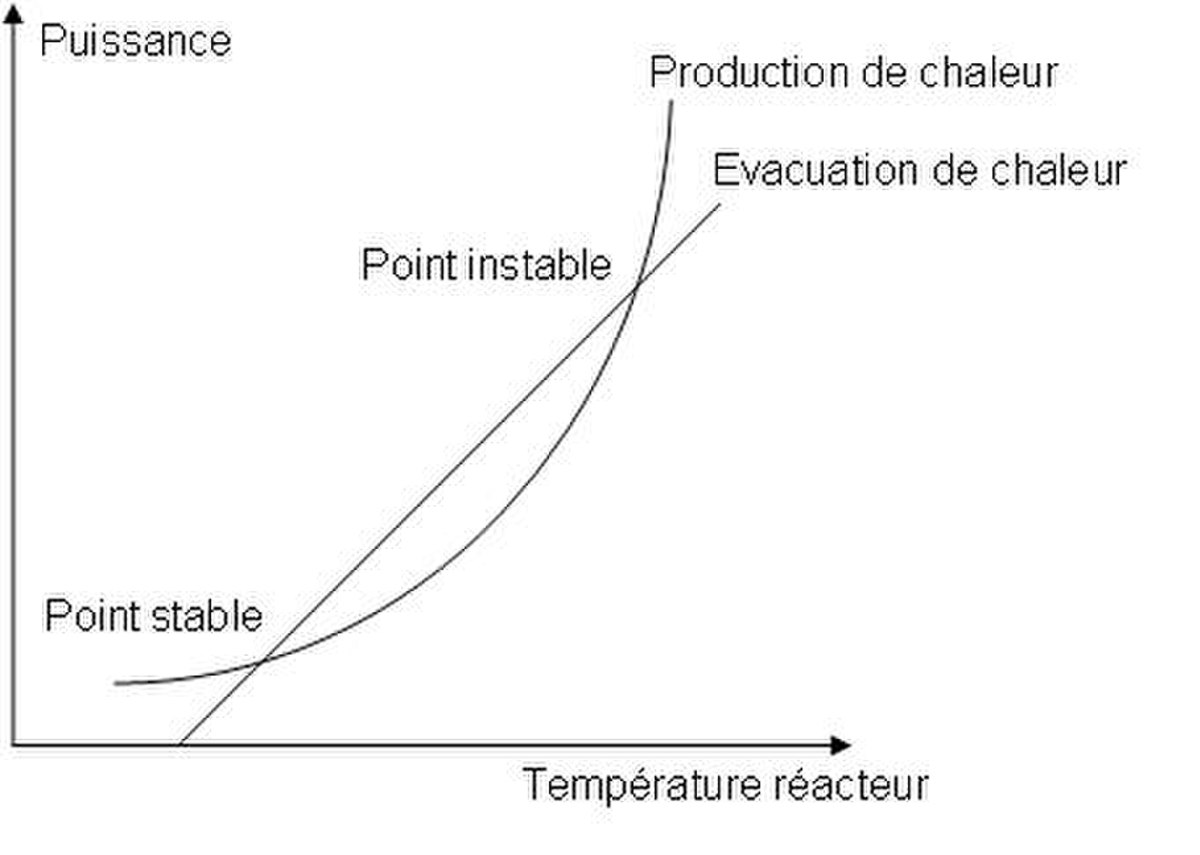
Le réacteur ne pourra être conduit de manière sûre uniquement si la puissance de refroidissement est supérieure ou égale à la puissance dégagée la réaction. Il est cependant important de réaliser que la puissance de refroidissement augmente linéairement avec la température, alors que celle libérée par la réaction augmente exponentiellement. Cela s'illustre bien de manière graphique, en traçant l'évolution de ces deux puissances en fonction de la température (Fig. 1).

Fig. 1 : Évolution de la puissance de refroidissement et de la puissance libérée par une réaction chimique en fonction de la température au sein du réacteur.

Un tel diagramme comme représenté en figure 1 est appelé diagramme de Semenov. La courbe exponentielle correspond à la production de chaleur, qui suit la loi d'Arrhenius, alors que la droite, de pente UA, donne la puissance du refroidissement, qui augmente linéairement avec la différence entre la température du manteau et celle du réacteur. À noter que la puissance de refroidissement vaut zéro quand la température dans le réacteur est égale à celle du manteau caloporteur.

Un tel diagramme de Semenov montre qu'il existe deux points où la production de chaleur est égale à l'évacuation de chaleur, et où par conséquent la température reste stationnaire, puisque le terme d'accumulation de chaleur s'annule. De ces deux points, un seul est dit stable, à savoir le premier. En effet, si la température vient à augmenter à partir de ce point, l'évacuation de chaleur devient supérieure à la production, ce qui a pour conséquence de faire revenir la température à son point stationnaire. La situation est similaire si la température vient subitement à baisser. Il en va du contraire pour l'autre point où la production et l'évacuation de chaleur sont égales. À partir de ce point, si la température augmente, il ne sera plus possible de maîtriser la température dans le réacteur : c'est l'emballement. On appelle par conséquent ce deuxième point point de non-retour.

On peut voir qu'il est possible de repousser le point de non-retour en augmentant la pente de la droite correspondant à la puissance de refroidissement, à savoir UA, le coefficient global de transfert thermique, en essayant par exemple d'augmenter l'aire de contact.