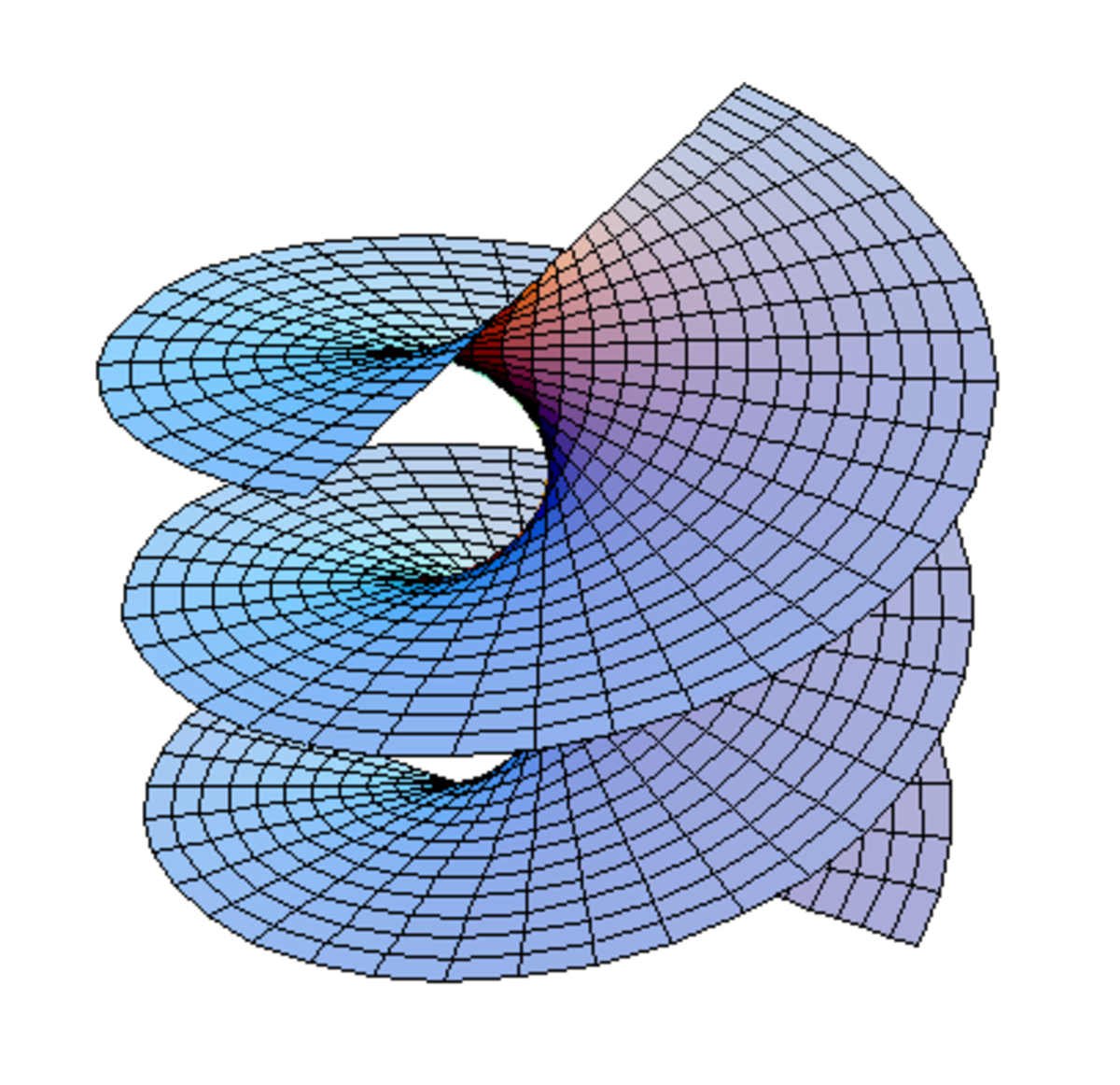
Surface minimale - Définition

Propriétés mathématiques

Courbure nulle

Équation aux dérivées partielles

Une surface de R³ peut localement après changement de coordonnées (euclidiennes) être représentée comme le graphe d'une fonction réelle à deux variables u et v. Plus précisément, la surface devient l'ensemble des points de coordonnées :

,

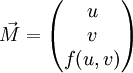
et en utilisant les notations et , l'équation locale d'Euler-Lagrange se réécrit :

.

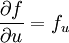
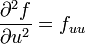
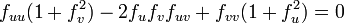
Cette équation donne une relation non évidente entre les dérivées partielles de f aux premier et second ordre : c'est un exemple d'équations aux dérivées partielles.

Exemples : La seule famille de solutions de la forme z = f(v / u) en est l'hélicoïde. La seule famille de solution de la forme z = f(u) + g(v) est une surface de Scherk.

• Même si cela peut paraître contre-intuitif, il n'y a pas unicité de solution au problème de Plateau. En d'autres termes, il n'existe pas toujours qu'une unique surface minimale s'appuyant sur un contour donné. Voici quelques éléments sur le nombre de surfaces minimales par contour:
  • Si le contour est une courbe plane, il ne borde qu'une surface minimale. De même s'il se projette simplement sur un plan suivant une courbe convexe (Rado, 1932).
  • Un contour dont la courbure totale est inférieure à 4π ne peut border qu'une surface minimale du type du disque.
  • Une courbe analytique ne peut border qu'un nombre fini de surfaces d'aire minimale.

Application de la théorie de Morse

La théorie de Morse se relève assez efficace pour compter les points critiques ; elle est célèbre pour avoir donné les inégalités de Morse qui permettent d'obtenir des estimations pour le nombre de points critiques d'une fonction définie sur un espace compact de dimension finie. Les surfaces de courbure nulle se présentent comme les points critiques de l'aire ou du volume. Il est tentant d'appliquer la théorie de Morse : cependant, les variations sur les surfaces impliquent nécessairement une étude en dimension infinie. La compacité ne peut plus être invoquée pour des raisons topologiques fondamentales.

Toutefois, une théorie analogue est réalisable et fournit l'identité:

,

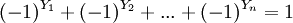
où n est le nombre de surfaces minimales distinctes, et les Y_n des entiers, nombres caractéristiques associés à chaque surface minimale.

Exemples

L'hélicoïde

• La caténoïde;
• La gyroïde;
• L'hélicoïde;
• La surface de Bour;
• La surface de Catalan;
• La surface de Costa;
• La surface d'Enneper;
• La surface d'Hennenberg;
• La surface d'Hoffman;
• Les surfaces de Scherk;
• La trinoïde.

La sphère, qui possède une courbure moyenne constante non-nulle, n'est pas une surface minimale au sens restrictif du terme. Elle vérifie cependant une autre propriété de minimisation : elle est la surface d'aire minimale enfermant un volume donné (lire à ce sujet Théorème isopérimétrique).

Application à la physique

Capillarité

Une caténoïde réalisée avec un film de savon

Dans certains cas, on peut matérialiser une surface minimale par un film de savon. En effet, un film de savon tend à minimiser son énergie potentielle ce qui revient à diminuer sa surface. Plus précisément, il obéit à l'équation de Laplace-Young : , où désigne la différence de pression entre les deux faces de la surface, la tension superficielle, caractéristique du liquide dont est constituée cette surface, et la courbure moyenne. Dans le cas d'un film de savon libre, la pression de l'air est la même de chaque côté, donc , par conséquent la courbure moyenne est nulle : on retrouve la définition mathématique de la surface minimale.

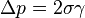
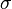
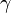
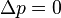
Cette représentation a toutefois d'intéressantes limites. En effet, ne peuvent être représentées de cette manière que des équilibres stables de l'énergie potentielle. Imaginons un contour en forme de "chips". Trois surfaces minimales peuvent s'appuyer sur ce contour, mais seules deux correspondent à des films de savons : la troisième est un équilibre instable, un film de savon "fantôme", c'est le cas correspondant par exemple à une surface d'Enneper.

Coût des matériaux

Stade Olympique de Munich

En architecture, l'utilisation de surfaces minimales permet à la fois de minimiser la quantité de matériaux utilisés et de mieux gérer les contraintes physiques en mimant un film de savon sur une armature. Un exemple frappant en est le stade olympique de Munich, qui date de 1972.