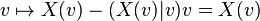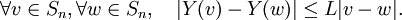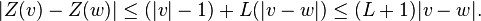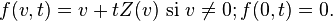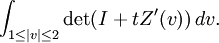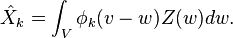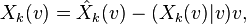Théorème de la boule chevelue - Définition
La liste des auteurs de cet article est disponible ici.
Énoncé
La sphère réelle de dimension n > 0 est la partie de
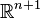
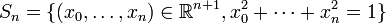
On munit cet ensemble de la topologie induite par la distance euclidienne. Cet espace topologique est une sous-variété connexe et compacte de dimension n. Intuitivement, si v est un vecteur unitaire, donc un point de Sn, la sphère peut au voisinage de v être approchée par l'hyperplan affine de
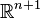
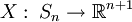
Théorème de la boule chevelue — Si n est un entier pair au moins égal à 2, tout champ de vecteurs continu X sur la sphère réelle Sn s'annule en un point au moins : il existe v (dépendant de X) tel que : X(v) = 0.
En dimension impaire, il existe des champs de vecteurs continus et mieux encore, analytiques, qui ne s'annulent en aucun point. On construit un exemple en identifiant
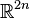
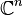
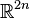
Démonstrations en dimension quelconque
Une démonstration très analytique est due à John Milnor. Dans l'article où il expose la preuve qui va suivre, Milnor évoque la méthode d'Asimov, mais l'article d'Asimov fait appel à des notions beaucoup plus avancées que celles qui seront présentées ici, et ne donne par conséquent pas de lumières élémentaires sur la source de cette surprenante démonstration. Une version un peu différente de la démonstration est donnée par C. A. Rogers.
La démonstration de Milnor est une démonstration par l'absurde, reposant sur la construction d'une transformation particulière dépendant d'un paramètre réel t et du champ de vecteurs considéré.
Afin de pouvoir utiliser des outils d'analyse, il faut supposer que le champ de vecteurs tangents est continûment différentiable, et donc, à la fin du raisonnement, on se sert d'un processus d'approximation.
La transformation dépendant de t envoie une sphère de rayon r sur une sphère de rayon
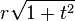
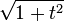
D'autres démonstrations sont fondées sur des notions plus savantes de topologie algébrique. Une démonstration classique utilise la caractéristique d'Euler-Poincaré. C'est un nombre qu'on peut obtenir par des méthodes combinatoires pour des ensembles qu'il est possible d'approcher par triangulation. Il permet dans certains cas (théorème de Poincaré-Hopf) de compter le nombre de points d'annulation d'un champ de vecteurs sur une variété. Une autre démonstration provient des propriétés de l'homotopie : on peut prouver que sur une sphère de dimension paire, l'application antipodale
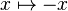
On note X un champ de vecteurs tangents continu sur Sn. Ce champ de vecteurs X est une fonction définie sur la sphère Sn et à valeurs dans l'espace euclidien V de dimension n + 1, avec n pair. On va démontrer au moyen d'un raisonnement par l'absurde qu'il s'annule forcément en au moins un point v de la sphère. On notera | v | la norme euclidienne d'un vecteur v de X, et (v | w) le produit scalaire euclidien de v et w, appartenant à X.
Cas d'un champ de vecteurs X continûment différentiable
Un champ X de vecteurs tangents à la sphère Sn est continûment différentiable, s'il est la restriction à Sn d'un champ continûment différentiable défini au voisinage de Sn. Comme ici, nous sommes dans une géométrie très simple, il suffit que
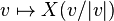
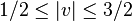
Tangent implique que, quel que soit v dans la sphère, X(v) est orthogonal à v.
Supposons donc que X ne s'annule jamais sur la sphère Sn. Comme X est continûment différentiable, sa norme | X | est aussi continûment différentiable sur la sphère et non nulle. Par conséquent, Y = X / | X | est un champ tangent, continûment différentiable et pour tout v, Y(v) est de norme 1. On dit aussi qu'il est unitaire.
Comme
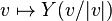
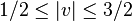
On définit un champ de vecteurs homogène de degré 1 sur tout V en posant
-
- Z(v) = | v | Y(v / | v | ),
et on va montrer que Z est lipschitzien. Supposons tout d'abord
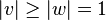
-
- Z(v) − Z(w) = | v | Y(v / | v | ) − Y(v / | v | ) + Y(v / | v | ) − Y(w / | w | ),
d'où, en vertu de l'inégalité triangulaire,
Par homogénéité, on obtient le cas général.
Définissons une fonction f sur V x ]0,1] par la formule suivante:
On voit que la fonction f est homogène de degré 1 par rapport à v. De plus, la norme de f(v,t) est facile à calculer, grâce au théorème de Pythagore:
-
- | f(v,t) | 2 = | v | 2(1 + t2).
En d'autres termes, l'image par f(.,t) de la sphère de centre 0 et de rayon r est incluse dans la sphère de centre 0 et de rayon
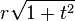
On va montrer qu'en fait cette image est toute la sphère ci-dessus. En vertu de l'homogénéité de f(v,t) par rapport à v, il suffit de le montrer pour une seule valeur de r, et on choisit
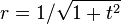
-
- v = w − tZ(v),
pour w donné, de norme 1.
L'idée consiste à utiliser le théorème du point fixe strictement contractant. On pose
-
- g(v,t) = w − tZ(v).
Attention: pour alléger les notations, on ne met pas w dans les arguments de g, et on le considère comme une constante.
La fonction g(.,t) envoie l'espace euclidien, qui est complet, V dans lui-même. Elle est lipschitzienne, de rapport t(L + 1). Par conséquent, si t est strictement inférieur à 1 / (L + 1), g(.,t) est une contraction stricte de V dans lui-même. Elle possède donc un unique point fixe, satisfaisant l'équation g(v,t) = v. Donc v est solution de f(v,t) = w. En particulier, d'après le calcul de la norme de f(v,t) effectué ci-dessus, on constate que | w | 2 = | f(v,t) | 2 = (1 + t2) | v | 2, et donc l'image de la sphère de rayon
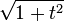
Par homogénéité, ceci démontre que f(.,t) envoie la sphère de rayon r sur la sphère de rayon
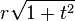
On calcule maintenant de deux manières différentes le volume de l'image par f(.,t) de la couronne solide de centre 0 et de rayons 1 et 2.
D'une part, cette image est la couronne solide de centre 0 et de rayons
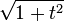
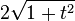
-
- ωn + 1(2n + 1 − 1)(1 + t2)(n + 1) / 2,
avec ωn + 1 le volume de la boule unité en dimension n + 1.
D'autre part, on sait dériver f(v,t) par rapport à v:
-
- f'v(v,t) = I + tZ'(v),
puisque Z est continuûment différentiable en dehors de 0. Ici, I est simplement l'application linéaire identité dans V. Par la formule du changement de variable dans les intégrales multiples, le volume de la boule est donc donné par :
Le déterminant est bien défini dans la formule ci-dessus, puisque Z'(v) est une application linéaire de V dans lui-même, paramétrée par v. On remarque que le déterminant ne change pas de signe, parce que f(.,t) est un difféomorphisme. Par continuité, il vaut 1 pour t nul, et donc il est partout positif. Il est donc inutile de mettre une valeur absolue.
On constate que la première expression du volume est irrationnelle par rapport à la variable t, puisque n est pair, alors que la deuxième est polynomiale par rapport à cette même variable. C'est la contradiction désirée, on a bien montré qu'un champ continûment différentiable tangent à la sphère Sn s'annule forcément en un point.
Cas général
On suppose cette fois-ci que X est un champ tangent continu sur la sphère Sn.
On peut approcher ce champ uniformément par une suite de champs tangents continûment différentiables
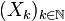
D'après l'étape précédente, pour chaque k, on peut trouver un vk dans Sn pour lequel Xk(vk) s'annule.
Les points vk appartenant à l'ensemble compact Sn, on peut trouver une sous-suite convergente de la suite des vk, ou, ce qui revient au même, une partie infinie K de
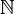
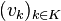
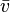
Il est immédiat que, le long de K, Xk(vk) converge vers
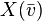
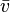
Approximation continûment différentiable d'un champ de vecteurs tangent continu
Soit φ une fonction de V dans
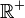
- φ est continûment différentiable;
- le support de φ, c'est-à-dire l'adhérence de l'ensemble de tous les pionts où φ n'est pas nul est inclus dans la boule de centre 0 et de rayon 1;
- l'intégrale de φ sur V vaut 1.
Un tel φ est facile à construire: on choisit tout d'abord une fonction ψ continûment dérivable, positive ou nulle sur
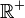
| I = | ∫ | ψ( | v | )dv. |
| V |
On vérifie que la fonction φ ainsi définie a les propriétés requises.
On pose, pour k un entier positif
-
- φk(v) = kφ(kv),
et on définit
On montre alors que les
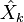
Mais a priori, il n'y a pas de raison que les
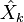
Le champ Xk est tangent à la sphère, et il converge uniformément vers le champ