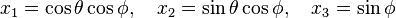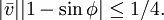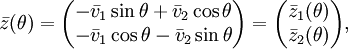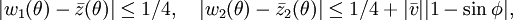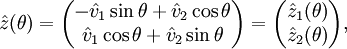Théorème de la boule chevelue - Définition
La liste des auteurs de cet article est disponible ici.
Formalisation de la démonstration visuelle
Cette formalisation sera d'abord géométrique, puis analytique pour ceux qui se sentent plus sûr des questions d'orientation quand tout est écrit. On raisonne par l'absurde, en supposant qu'il existe un champ de vecteur tangent v(x) continu et ne s'annulant nulle part sur la sphère de dimension S2.
Version géométrique
On choisit sur la sphère un pôle nord et un pôle sud, ainsi qu'une orientation. On peut alors parler des parallèles de la sphère et les orienter de façon continue. De plus, on peut définir un repère mobile tangent sur la sphère, en dehors des pôles nord et sud. Le premier vecteur du repère mobile est tangent au parallèle passant par ce point et orienté dans la direction de parcours des parallèles, et le second vecteur est perpendiculaire au premier, avec un sens choisi pour se conformer à l'orientation de la sphère. Le champ de vecteur v admet une décomposition dans le repère mobile. On peut donc associer à tout parallèle un nombre d'enroulement : c'est le nombre d'enroulement du champ de vecteur dans le repère mobile le long de ce parallèle. Ce nombre est bien défini puisque le champ de vecteur ne s'annule pas. Il dépend continûment de la latitude du parallèle, d'après les résultats standard sur la continuité du nombre d'enroulement, et il est entier. Il est donc constant.
On calcule ce nombre d'enroulement au voisinage du pôle nord. Certes, le repère mobile cesse d'être défini au pôle nord, mais pour pallier cette difficulté, on dilate un parallèle proche du pôle nord en un cercle de rayon unité, et on projette à la fois le champ de vecteur v et le repère mobile sur le plan tangent au pôle nord. L'orientation de ce plan tangent est déduite de celle de la sphère. Par continuité, le nombre d'enroulement ne change pas lors de cette transformation. A la limite, le repère mobile transformé tourne une fois autour du pôle, dans le sens des parallèles, et donc le champ de vecteurs tourne - une fois dans le repère mobile. Le nombre d'enroulement vaut donc m et m vaut + 1 ou − 1, suivant le choix d'orientation des parallèles.
Avec le même raisonnement au voisinage du pôle sud, le repère mobile tourne une fois autour du pôle sud dans le sens des parallèles, mais pour maintenir une orientation cohérente avec celle de la sphère, en tant que plan dans l'espace à trois dimensions, le plan tangent au pôle sud est orienté dans le sens opposé du plan tangent au du pôle nord, et donc le nombre d'enroulement du champ est − m. On a la contradiction souhaitée.
Version analytique
On note x le point courant de la sphère et v(x) le champ de vecteurs. On paramétrise la sphère en coordonnées polaires, en la supposant de rayon 1:
avec 0≤θ<2π et − π / 2≤ φ≤π / 2. On remarque que ce paramétrage ne définit ni une bijection ni a fortiori un difféomorphisme.
En chaque point de la sphère distinct des pôles nord et sud, on introduit un repère mobile formé de deux vecteurs tangents à la sphère. Le premier vecteur, e1(θ,φ), a pour coordonnées ( − sinθ,cosθ,0) et le deuxième, e2(θ,φ), a pour coordonnées ( − sinφcosθ, − sinφsinθ,cosφ). Il est immédiat que cette base dépend continûment de θ et φ pour
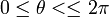
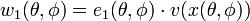
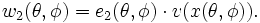
Ces coordonnées dépendent continûment de θ et φ, sur
![[0,2\pi]\times]-\pi/2,\pi/2[](https://static.techno-science.net/illustration/Definitions/autres/8/8b231ae143a06b22ad71bd31940d0d06_ac811d62d734b10192be2d133250a90f.png)
Pour tout φ compris strictement entre -π/2 et π/2, on peut donc définir le nombre d'enroulement du champ de vecteur
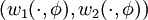
![\phi\in]-\pi/2,\pi/2[](https://static.techno-science.net/illustration/Definitions/autres/3/3b449fdcfe16044050fe70b64874a75d_2339925da9b10141d401e4eeb39db170.png)
On va maintenant calculer le nombre d'enroulement du champ de vecteur au voisinage des pôles nord et sud, afin d'arriver à une contradiction.
Soit
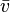
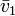
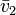
-
si 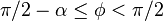
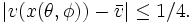
On peut aussi choisir α assez petit pour avoir
Si l'on note
alors le calcul donne
pour
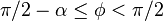
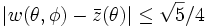
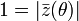
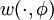
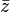
Le même raisonnement au voisinage du pôle sud montre que si l'on pose
alors pour φ assez proche de − π / 2, le nombre d'enroulement de
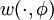
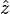
On a bien la contradiction souhaitée.