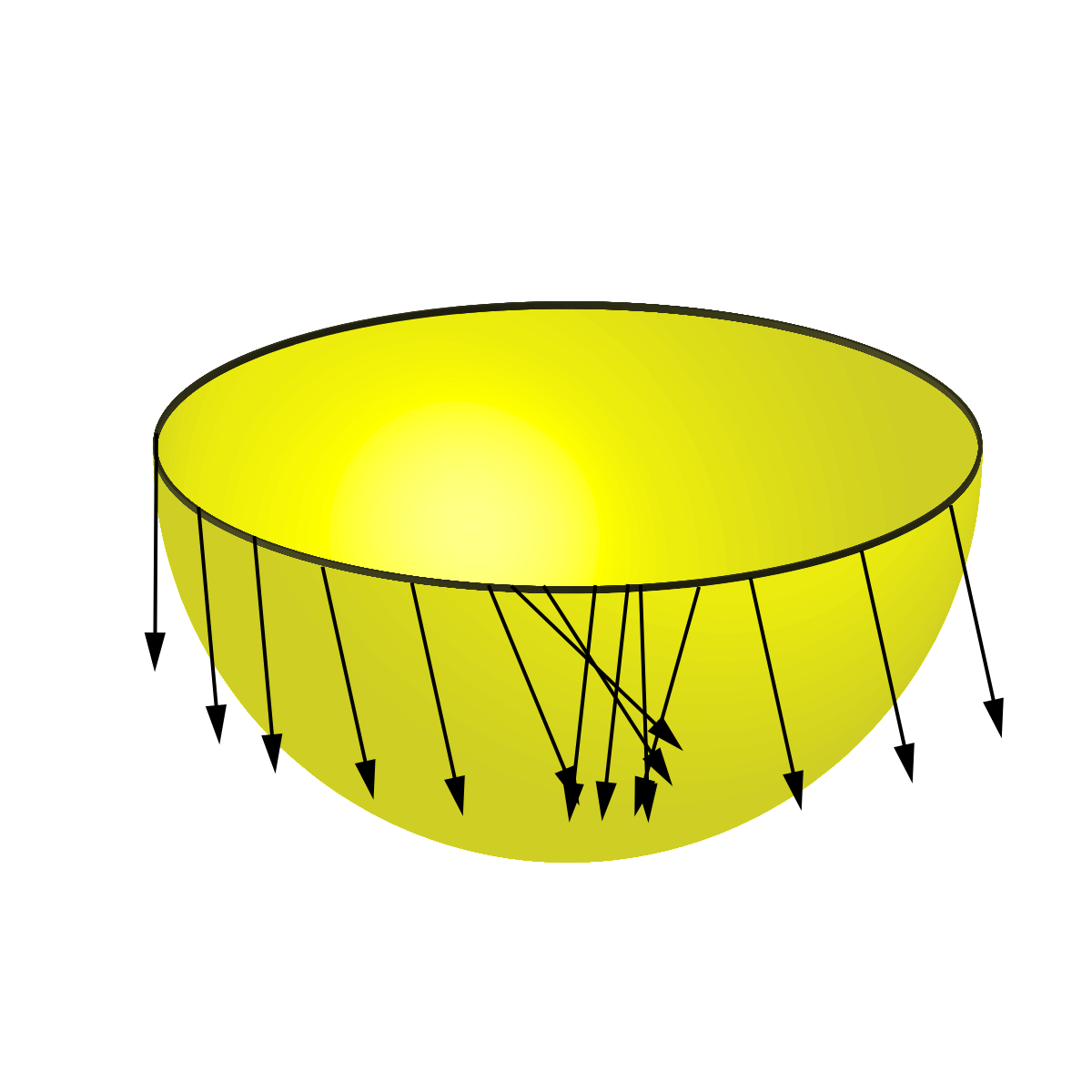
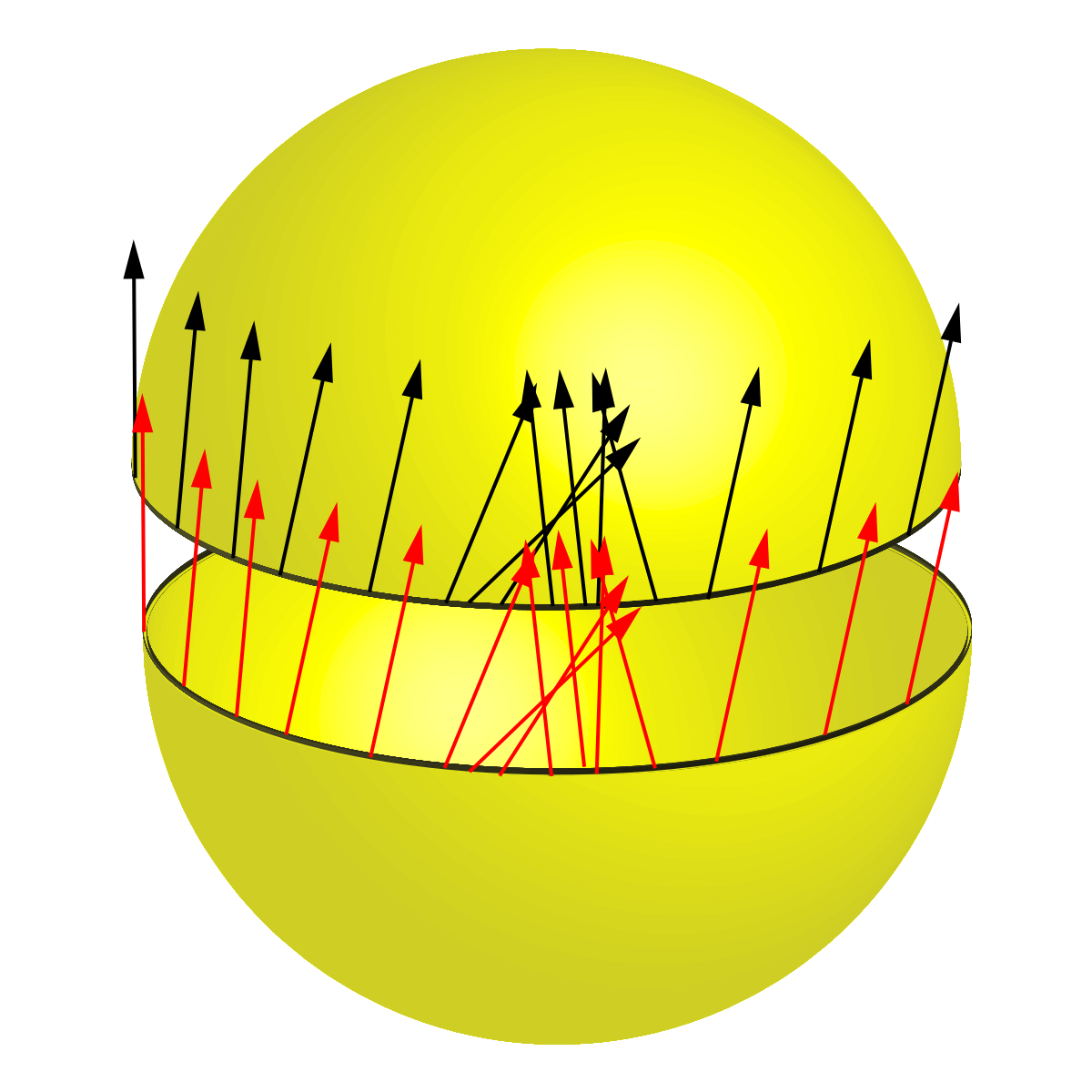
Théorème de la boule chevelue - Définition

Bibliographie

• (en) J. W. Milnor, Topology from the differentiable viewpoint Princeton Univ. 1997
• (fr) N. E. Chinn W. G. Steenrod Topologie élémentaire Dunod 1991
• (en) M. Eisenberg, R. Guy, A Proof of the Hairy Ball Theorem The American Mathematical Monthly Vol. 86, No. 7 (Aug. — Sep., 1979), pp. 571–574

Conséquences

Les conséquences du théorème sont nombreuses et ne se limitent pas aux mathématiques.

Fusion nucléaire

Une application technologique est donnée par la fusion nucléaire civile. L'objectif est d'obtenir de l'énergie à partir d'une réaction de fusion de même nature que celle qui produit l'énergie des étoiles. Une des difficultés provient du fait que la matière, à l'état de plasma, doit être confinée à une température et une pression trop forte pour qu'aucun matériau ne puisse résister.

Une solution envisagée est le confinement du plasma par un champ magnétique. On parle de confinement "magnétique", par opposition au confinement dit "inertiel", également en cours d'expérimentation, qui ne repose pas sur l'électromagnétisme mais sur des techniques à base de lasers. Un exemple plus précis pourrait être le tokamak, littéralement la contraction (en Russe) de "Chambre de confinement magnétique toroïdale". Si une forme sphérique semble la solution la plus naturelle pour ce type de réacteur, le théorème de la boule chevelue implique qu'une telle géométrie est impossible. Il existerait en effet un point à la surface où le champ magnétique de confinement s'annulerait. En un tel point, le plasma ne serrait plus confiné par le champ magnétique, et l'objectif de réaction entretenue ne serait pas atteint.

C'est pour cette raison que la forme retenue pour les tokamak est comme son nom l'indique un tore, c'est-à-dire l'unique géométrie qui n'admet pas d'équivalent du théorème de la boule chevelue. Le projet Joint European Torus est un exemple.

Météorologie

L'oeil d'un cyclone correspond à une singularité de même nature que celle qu'impose le théorème de la boule chevelue.

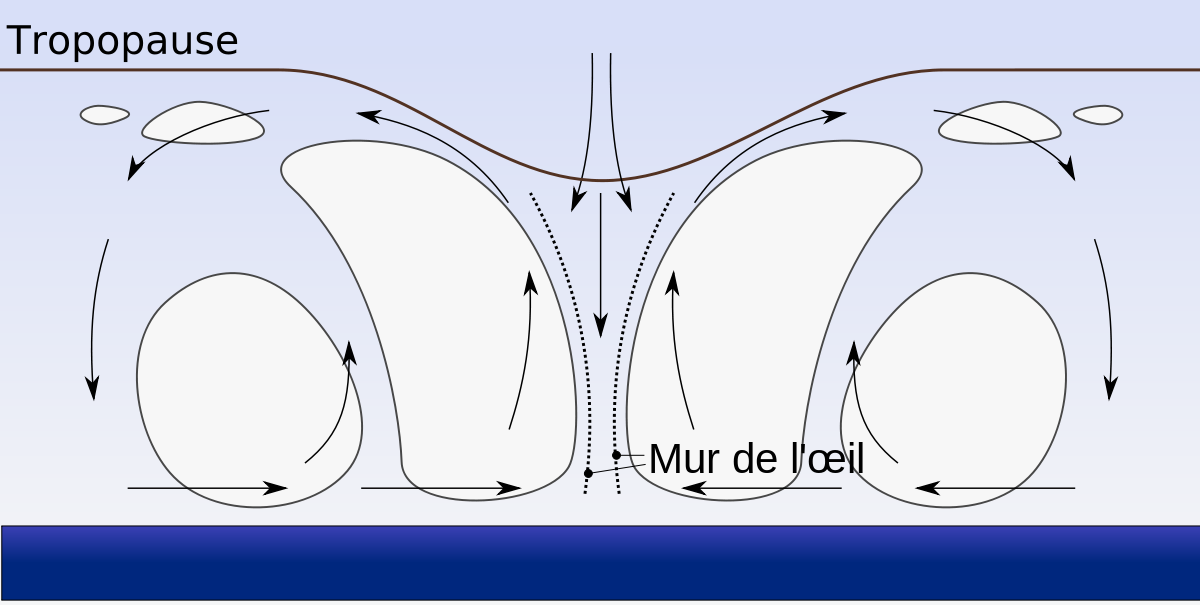
Le théorème de l'article possède une conséquence météorologique. Le vent, sur la surface du globe se décrit par une fonction continue. Une modélisation schématique le représente par un champ de vecteurs bi-dimensionnel. Relativement au diamètre de la terre, la composante verticale du vent est en effet négligeable.

Une première manière de satisfaire le théorème de la boule chevelue consiste à imaginer l'existence d'un point de la surface terrestre absolument sans vent. Une telle hypothèse est physiquement irréaliste.

Une modélisation physiquement plus en cohérence avec l'observation implique l'existence d'un complexe cyclonique ou anticyclonique. Le théorème de l'article impose l'existence permanente d'un point sur terre ou le vent se modélise par un système tourbillonnant avec, en son centre un oeil où la composante horizontale du vent est nulle. Cette conséquence est de fait observée dans la réalité.

Le théorème n'offre aucune indication sur la taille de l'œil ou sur la puissance des vents qui l'entourent.

Théorème du point fixe de Brouwer

On peut démontrer le théorème du point fixe de Brouwer à partir du théorème de la boule chevelue. Il s'énonce ainsi :

Démonstration visuelle pour le disque

La démonstration est encore une fois une démonstration par l'absurde. Supposons qu'il existe une application continue f du disque unité dans lui-même, telle que f(x) soit distinct de x quel que soit x dans le disque unité. On va fabriquer une boule chevelue sans épi ni calvitie, et obtenir ainsi une contradiction.

Si on a une application f sans point fixe, alors chaque point x du disque permet de définir un vecteur non nul, le vecteur f(x) − x.

Maintenant, on prend une balle de tennis, on coupe soigneusement la peau de la balle le long de l'équateur, et on détache chacune des demi-sphères de peau. Comme elles sont en caoutchouc, on peut les déformer et les appliquer soigneusement tour à tour sur le demi-disque.

Le disque avec les vecteurs f(x) − x attachés chacun à leur origine x.

La balle de tennis incisée le long de son équateur avec son noyau en caoutchouc.

L'hémisphère du haut rendu transparent et déplacé au-dessus du disque.

On aplatit l'hémisphère du haut, transparent, sur le disque.

Une fois la première demi-sphère appliquée sur le disque, il est facile de dessiner en chaque point un vecteur, qui a la même direction que f(x) − x, mais qui est de norme 1, pour ne pas se compliquer la tâche. On relâche alors la demi-sphère, et par un miracle mathématique, les vecteurs dessinés deviennent des vecteurs tangents non nuls. On fait la même chose pour le deuxième demi-hémisphère : on copie le champ de vecteur, puis on le relâche, si bien qu'il reprend sa forme, et il est muni d'un champ de vecteurs tangent qui ne s'annule pas.

L'hémisphère du haut, toujours aplati, mais avec copie des vecteurs.

L'hémisphère du haut reprend sa forme, avec les vecteurs collés.

Au bord de chacun des deux demi-hémisphères, le champ de vecteur se trouve dans un plan vertical. Si on remettait les deux hémisphères sur la balle de tennis, on n'aurait pas un champ continu. Mais cela se corrige : sur le deuxième hémisphère, on transforme le champ de vecteur de la façon suivante : en chaque point, le champ se trouve dans un plan tangent, et dans ce plan, on reflète le vecteur par rapport à la tangente au parallèle en ce point.

L'hémisphère du bas est d'abord l'image de celui du haut dans un miroir horizontal. On n'a représenté que les vecteurs du devant.

Maintenant, les vecteurs attachés à l'hémisphère du bas sont symétrisés. On n'a représenté que les vecteurs du devant.

L'hémisphère du bas prêt à être recollé à l'hémisphère du haut. Ses vecteurs sont en rouge pour faciliter la lecture de la figure, et ils sont en continuité avec ceux de l'hémisphère du haut.

A ce moment-là, on recolle les deux hémisphères sur la balle, et cette fois-ci leurs champs tangents se raccordent continûment, fournissant ainsi une chevelure continue et sans calvitie à la boule, ce qui donne la contradiction désirée.

Démonstration dans le cas général pour n'importe quelle boule

La démonstration générale est une formalisation de la démonstration visuelle qui précède, dans le cas des boules de dimension paire. Le cas de dimension impaire est déduit du cas de dimension paire par abaissement dimensionnel.

Un corollaire anecdotique

Le résultat suivant d'algèbre linéaire est bien plus élémentaire et général (il reste immédiat quand on remplace R par n'importe quel anneau commutatif de caractéristique différente de 2), mais peut être vu, dans le cas particulier du corps des réels, comme un corollaire du théorème de la boule chevelue :

Une matrice antisymétrique A d'ordre impair à coefficients dans R n'est pas inversible (car son déterminant est nul). Ou encore : la forme bilinéaire antisymétrique associée est dégénérée.

En effet, pour tout vecteur v de l'espace euclidien V sur lequel agit A, on a : (Av | v) = − (v | Av) = − (Av | v) et donc Av.v = 0. En particulier, X(v) = Av définit par restriction un champ de vecteurs continu sur la sphère unité de V, qui est une sphère de dimension paire. Ce champ admet un point d'annulation v. Ce vecteur unitaire v appartient donc au noyau de A.