Théorie du chaos - Définition

Introduction

La théorie du chaos traite des systèmes dynamiques rigoureusement déterministes, mais qui présentent un phénomène fondamental d'instabilité appelé « sensibilité aux conditions initiales » qui, modulant une propriété supplémentaire de récurrence, les rend non prédictibles en pratique sur le « long » terme.

Introduction

Définition heuristique d'un système chaotique

Un système dynamique est dit chaotique si une portion « significative » de son espace des phases présente simultanément les deux caractéristiques suivantes :

• le phénomène de sensibilité aux conditions initiales.

• une forte récurrence.

La présence de ces deux propriétés entraîne un comportement extrêmement désordonné qualifié à juste titre de « chaotique ». Les systèmes chaotiques s'opposent notamment aux systèmes intégrables de la mécanique classique, qui furent longtemps les symboles d'une régularité toute puissante en physique théorique. La dynamique quasi-périodique d'un système intégrable semblait elle-même trouver son illustration parfaite dans les majestueux mouvements des planètes du système solaire autour du Soleil ; souvenons-nous que Voltaire, qui incita Émilie du Châtelet à entreprendre la traduction des Principia Mathematica de Newton, parlait de Dieu comme du « Grand Horloger »…

Qu'est-ce que la « théorie du chaos » ?

Au cours de son histoire, la physique théorique s'était déjà trouvée confrontée à la description de systèmes complexes macroscopiques, comme un volume de gaz ou de liquide, mais la difficulté à décrire de tels systèmes semblait découler du très grand nombre de degrés de liberté internes du système à l'échelle microscopique (atomes, molécules). La mécanique statistique avait dans ce cas permis de rendre compte de façon satisfaisante des propriétés macroscopiques de ces systèmes à l'équilibre. Ce fut donc une grande surprise lorsqu'on s'aperçut à la fin du XIX^e siècle qu'une dynamique d'une grande complexité pouvait résulter d'un système simple possédant un très petit nombre de degrés de liberté, pourvu qu'il possède cette propriété de sensibilité aux conditions initiales.

La théorie du chaos s'attache principalement à la description de ces systèmes à petit nombre de degrés de liberté, souvent très simples à définir, mais dont la dynamique nous apparaît comme très désordonnée.

La théorie du chaos est-elle née dans les années 1970 ?

Attracteur étrange de Lorenz (1963)

La réponse à cette question est : oui et non.

• Non, car le phénomène de sensibilité aux conditions initiales a été découvert dès la fin du XIX^e siècle par Henri Poincaré dans des travaux concernant le problème à N corps en mécanique céleste, puis par Hadamard avec un modèle mathématique abstrait aujourd'hui baptisé « flot géodésique sur une surface à courbure négative ». Cette découverte a entraîné un grand nombre de travaux importants, principalement dans le domaine des mathématiques. Ces travaux sont évoqués dans le paragraphe Développements historiques situé plus loin.

• Oui, car ce n'est véritablement que dans les années 1970 que la théorie du chaos s'est progressivement imposée sur le devant de la scène scientifique, opérant une rupture épistémologique forte. Le terme suggestif de « chaos » n'a d'ailleurs été introduit qu'en 1975 par les deux mathématiciens Tien-Yien Li et James A. Yorke. Le caractère tardif de ce changement de paradigme s'explique aisément : la théorie du chaos doit en effet sa popularisation aux progrès fulgurants de l'informatique à partir des années 1960-70. Cette science nouvelle a en effet rendu accessible aux non-mathématiciens la visualisation directe de l'incroyable complexité de ces systèmes dynamiques, auparavant réservée aux seuls « initiés » capables d'absorber le formalisme mathématique idoine.

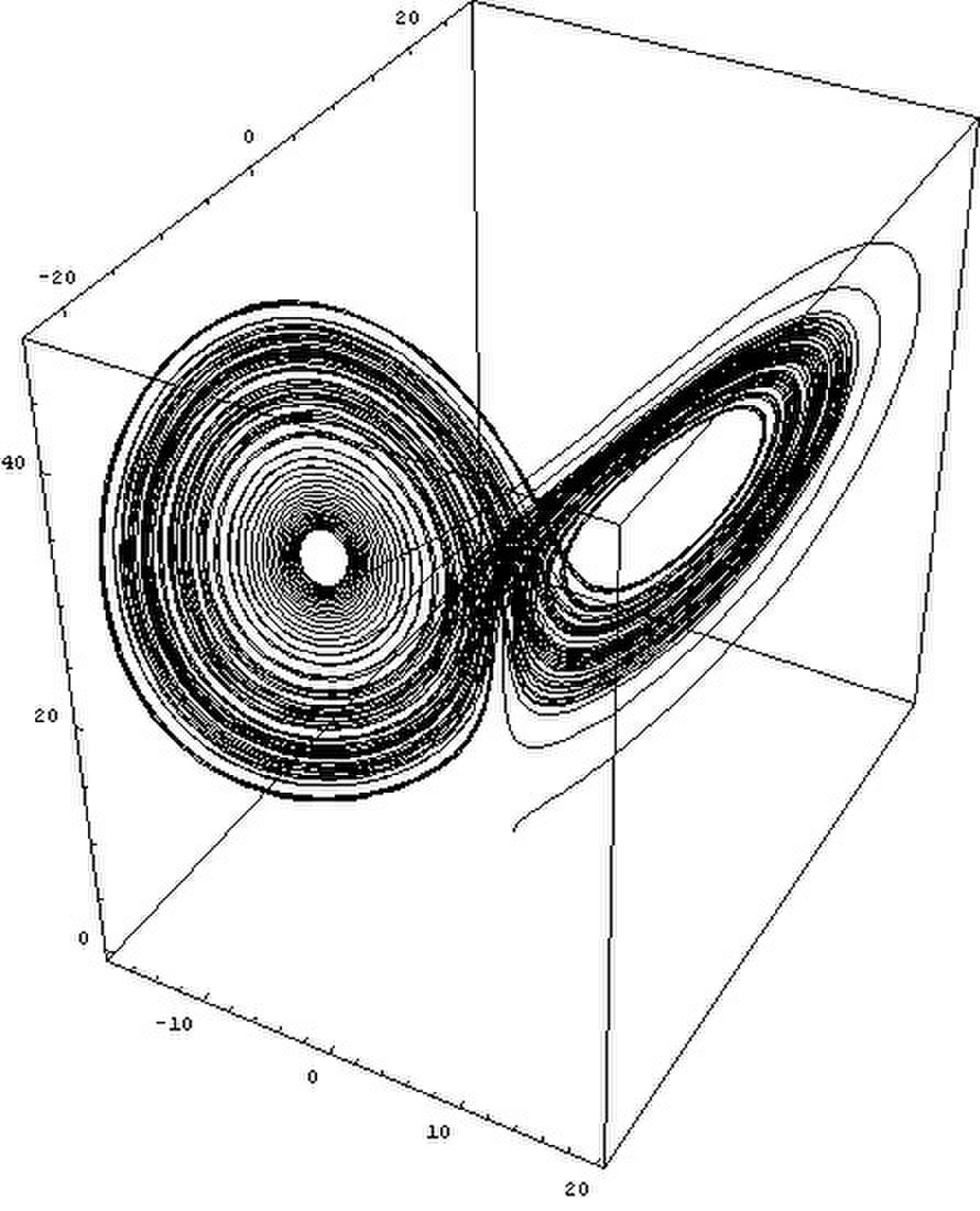
À titre d'illustration, la figure ci-contre est un exemple typique d'images produites par la théorie du chaos ; il s'agit ici d'un objet géométrique découvert par Lorenz en 1963, et baptisé depuis « attracteur étrange ». (Cet objet sera commenté plus bas, au paragraphe : Lorenz & la météorologie.)

La théorie du chaos est une véritable théorie scientifique, qui a su trouver de l'ordre caché sous le désordre apparent. Mais ce nouvel ordre est très différent de l'ordre ancien : au déterminisme implacable d'une dynamique intégrable quasi-périodique a succédé une description de nature fondamentalement probabiliste, caractérisée par l'existence d'invariants prenant la forme de mesures de probabilités, d'attracteurs, de dimensions fractales… Toutes les sciences, y compris sociales, sont concernées par ce changement de paradigme.