Parabole de sûreté - Définition

Soit un boulet B (lancé à une vitesse initiale Vo), tombant dans le vide, dans un champ de pesanteur uniforme g.

Sa trajectoire sera dans le plan vertical (O, Vo, g). Selon la célèbre loi de la chute libre énoncée en 1602 par Galilée (1568-1642), son mouvement ne dépend ni de sa masse, ni de sa densité.

Il est régi par la seule équation :

,

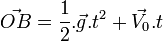
qui est l'équation d'une parabole en coordonnées affines (de vecteurs de base g et V°).

Pour un module V° donné, quelle que soit la direction donnée à la " hausse " du canon, certains points seront hors de portée du canon. L'ensemble de ces points forme une région du plan limitée par une courbe (C) qui " entoure " le point O ; au-delà de (C), " on est en sûreté ", d'où le nom de la courbe.

Dans le cas présent, (C) est une parabole, d'où le titre : parabole de sûreté :

En coordonnées polaires, en partant de l'apex H de la parabole, son équation est :

, avec (portée horizontale).

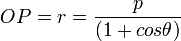
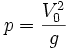
Démonstration

Elle a été donnée par Galilée, améliorée par Torricelli, son élève (de 1640 à 1642). La voici :

Soit φ = angle (OH,V°). Soit P le point de portée maximale,sur (C). Il faut démontrer, avec θ = 2φ, que OP = p/2cos²φ, avec p/2 = OH.

Soit OR = V°t , le mouvement comme rien ! et RP = -1/2 g t^2 la chute verticale.

Considérer le losange OPRQ de côtés égaux OP=RP=RQ=OQ = 1/2 g.t^2, de centre C : la cote z_C vaut OH ; alors on lit :

géométriquement, et

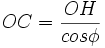
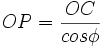
soit , CQFD.

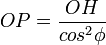
Note d'Histoire

Le père minime Mersenne (1588-1648) fut ébahi par une démonstration si simple, et adressa une lettre au jeune Huygens (1629-1695), alors jeune homme, qui répondit immédiatement qu'il en était " fort bien ainsi ".

Bien faire attention au fait que ce sont des problèmes de théoriciens : on est bien loin de se préoccuper de la trajectoire réelle d'un boulet.

En réalité, Torricelli est le premier à mettre la relativité galiléenne en acte : son idée ? Extrêmement simple, mais géniale : quelle que soit la position B1 du boulet B, à l'instant t1, avec la vitesse V1, il suffit de se placer dans le référentiel galiléen tangent pour retrouver une chute verticale B1B = 1/2 g (t-t1)^2. Ce sera pour la première fois sans doute le fameux dessin du " funiculaire à rochets " : le mobile poursuit sa course tangentielle , et retombe sur sa trajectoire, etc. Appris très jeune par Huygens, cela ne lui posera aucun problème de calculer ensuite l'accélération centripète du mouvement circulaire (encore qu'il préférât toujours parler de force centrifuge). Il n'y avait qu'un pas à franchir : ce fut Newton.

Relativité galiléenne ?

Mais encore bien plus : Torricelli a-t-il pu traiter formellement le problème de covariance galiléenne suivant : soit une vitesse nulle au départ. Intuitivement le corps tombe verticalement : OB = k f(t). Appliquons maintenant le principe d'inertie et celui de relativité galiléenne et l'invariance temporelle et locale des lois : pour 2 temps t1 et t2, on doit avoir :

OB(t1+t2) = V°(t1+t2) + k f(t1+t2) = OB1 + V1.t2 + k f(t2), avec OB1 = V°.t1 +k f(t1) et V1 = V° +k f '(t1).

Soit f(t1+t2) = f(t1) +f(t2) +f '(t1).t2

Comme t1 et t2 sont commutatifs, f'(t1).t2 = f'(t2).t1 : donc f'(t)/t=cste ; la vitesse est nécessairement fonction linéaire du temps : f'(t) = g.t : dans un champ invariant par position, c’est-à-dire produisant en tout point initial, de vitesse nulle, le même mouvement, alors la relativité galiléenne impose la linéarité temporelle de la vitesse : V(t) = g.t .

Personnellement, je serais heureuse de retrouver qui, le premier, a écrit un papier de ce goût-là : avis de recherche. merci d'avance.

(1,3,5,7...)

La suite est mieux connue : très habilement en construisant le diagramme des vitesses, Galilée retrouve la célèbre loi du trapèze : B1B2 = (V1+V2)/2 .(t2-t1) , soit des accroissements de distance comme 0+1, 1+2 , 2+3 ,3+4 , ... Nous préférons dire aujourd'hui un anachronique et sec z = 1/2 g t^2. Oui ! On n'a jamais le temps.

Et rajoutera Torricelli V(x) = sqrt(2gx); ou V2² − V1² = 2g(z1 − z2)

Soit V1^2 + 2g z1 = V^2 + 2g.z = cste = (2E° pour nous aujourd'hui): c'est la formule de Torricelli qu'il appliquera à l'écoulement de l'eau, par un raisonnement que perso, je n'ai jamais lu. Comme V^2 >0, on obtient un z maximum : c'est cette idée que Torricelli va transmettre au jeune Huygens via Mersenne : oui, ainsi va la science ; si j'ai pu voir plus loin c'est parce que j'étais juché sur des épaules de géants...