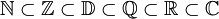Nombre - Définition
Un nombre est un concept caractérisant une unité, une collection d'unités ou une fraction d'unité.
Notions à distinguer
- Chiffre
Un chiffre est un caractère utilisé à l'écriture d'un nombre ou d'un numéro. L'erreur la plus fréquente est de confondre le chiffre avec le nombre. Les chiffres généralement utilisés pour l'écriture des nombres sont les chiffres arabes : {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
- Nombre
Les nombres sont utilisés pour résoudre des problèmes faisant intervenir des valeurs. Mais attention, un nombre n'est pas une quantité. C'est un objet mathématique qui répond à des lois précises.
Un nombre cardinal est un type de nombre particulier utilisé pour le dénombrement des ensembles. Il ne faut pas les confondre avec les adjectifs numéraux cardinaux.
Un nombre ordinal est un type de nombre particulier utilisé pour marquer l'ordre des éléments d'un ensemble. Il ne faut pas les confondre avec les adjectifs numéraux ordinaux. L'énumération avec les nombres ordinaux commence par " 0 ", tandis qu'avec les adjectifs numéraux ordinaux elle commence par premier ou " 1 ".
- Numéro
Un numéro est simplement une combinaison de chiffres qui ne respecte pas nécessairement une énumération et joue généralement le rôle d'une étiquette numérique.
Types de nombres
Il existe différents types de nombres. Les nombres les plus familiers sont les entiers naturels : 0, 1, 2, 3, … éléments de l'ensemble
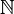
Si les entiers négatifs sont inclus, on obtient l'ensemble des nombres entiers relatifs

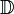
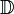
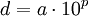


La division d'un entier relatif par un entier relatif non nul forme un nombre rationnel. L'ensemble de tous les nombres rationnels est noté
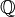
Si, dans l'ensemble, outre les éléments de



Les nombres réels peuvent être étendus aux nombres complexes, dont l'ensemble est noté

Nous avons donc une hiérarchie d'ensembles :
Les nombres complexes peuvent, à leur tour, être étendus aux quaternions, mais la multiplication des quaternions n'est plus commutative. Les octonions, à leur tour, étendent les quaternions, mais cette fois, l'associativité est perdue. Les sédénions étendent à leur tour l'ensemble des octonions.
En fait, les seules algèbres de division associatives à dimension finie sur

Les éléments des corps de fonctions algébriques de caractéristique finie ont été souvent interprétés de plusieurs manières comme une sorte de nombres par les théoriciens des nombres.
Histoire
Les nombres sont apparus dans cet ordre :
- Les entiers naturels,
- Les nombres rationnels positifs,
- L'invention du zéro,
- Les entiers relatifs,
- Les nombres rationnels,
- Les nombres irrationnels et les nombres réels,
- Les nombres complexes,
- Les nombres hypercomplexes (quaternions),
- Les nombres p-adiques,
- Les nombres réels transcendants et les nombres réels algébriques,
- Les nombres transfinis, constitués des ordinaux et cardinaux
- Les nombres hyperréels,
- Les nombres réels calculables,
- Les nombres surréels et pseudo-réels.
Ce n'est pas fortuit : on passe de la façon la plus simple de mesurer à des techniques beaucoup plus élaborées.
La compréhension des limites des nombres rationnels et de la nécessité des nombres irrationnels fut particulièrement douloureuse pour les pythagoriciens ; on dit même que cela scella la fin de cette École.
Les nombres complexes se sont imposés dans un premier temps comme un argument spécieux mais efficace pour résoudre les équations polynomiales (d'où le vocable d'" imaginaire " pour désigner certains d'entre eux), avant de finalement être reconnus comme des nombres à part entière.
Les nombres hypercomplexes furent inventés par Hamilton (quaternions) puis par Cayley (octonions) et les sédénions par la construction de Cayley-Dickson. À chaque composante d'un nombre hypercomplexe, on peut associer une base à plusieurs dimensions (4 pour les quaternions, 8 pour les octonions et 16 pour les sédénions). Il existe aussi les biquaternions.
L'apparition des nombres p-adiques est liée à la notion de valeur absolue, et sont très utilisés en théorie des nombres.
Les nombres hyperréels furent conçus pour résoudre certains problèmes de l'analyse et leur création par Abraham Robinson permit le développement de l'analyse non-standard. Les nombres pseudo-réels sont très semblables à l'ensemble plus vaste des hyperréels, mais la construction est différente.
Les opérations arithmétiques sur les nombres, telles que l'addition, la soustraction, la multiplication et la division sont généralisées dans la branche des mathématiques appelée algèbre abstraite dans laquelle on obtient les groupes, les anneaux et les corps.