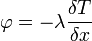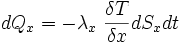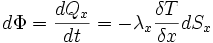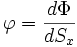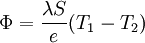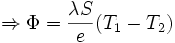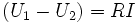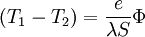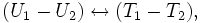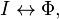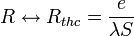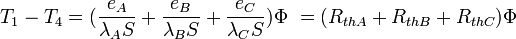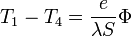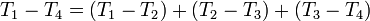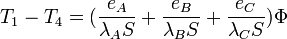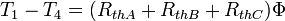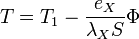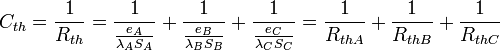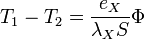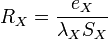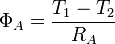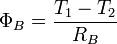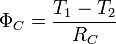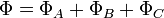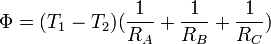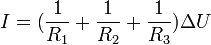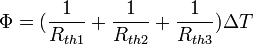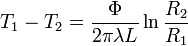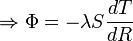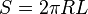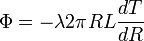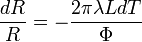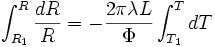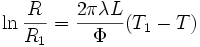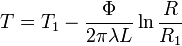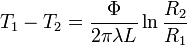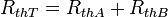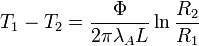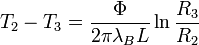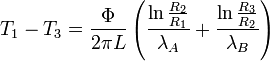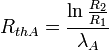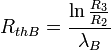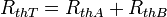Conduction thermique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

La conduction thermique est le mode de transfert de chaleur provoqué par une différence de température entre deux régions d'un même milieu ou entre deux milieux en contact sans déplacement appréciable de matière. C'est en fait l'agitation thermique qui se transmet de proche en proche, une molécule ou un atome cédant une partie de son énergie cinétique à son voisin (la vibration de l'atome se ralentit au profit de la vibration du voisin).

Généralités

Loi de Fourier

Ce transfert de chaleur spontané d'une région de température élevée vers une région de température plus basse obéit à la loi dite de Fourier (établie mathématiquement par Jean-Baptiste Biot en 1804 puis expérimentalement par Fourier en 1822).

La densité de flux de chaleur est proportionnelle au gradient de température.

$\varphi= - \lambda \frac{\delta T}{\delta x}\,$

La constante de proportionnalité λ est nommée conductivité thermique du matériau. Elle est toujours positive. Avec les unités du système international, la conductivité thermique λ s'exprime en J.m^-1.K^-1.s^-1 ou, soit des W.m^-1.K^-1.

Démonstration

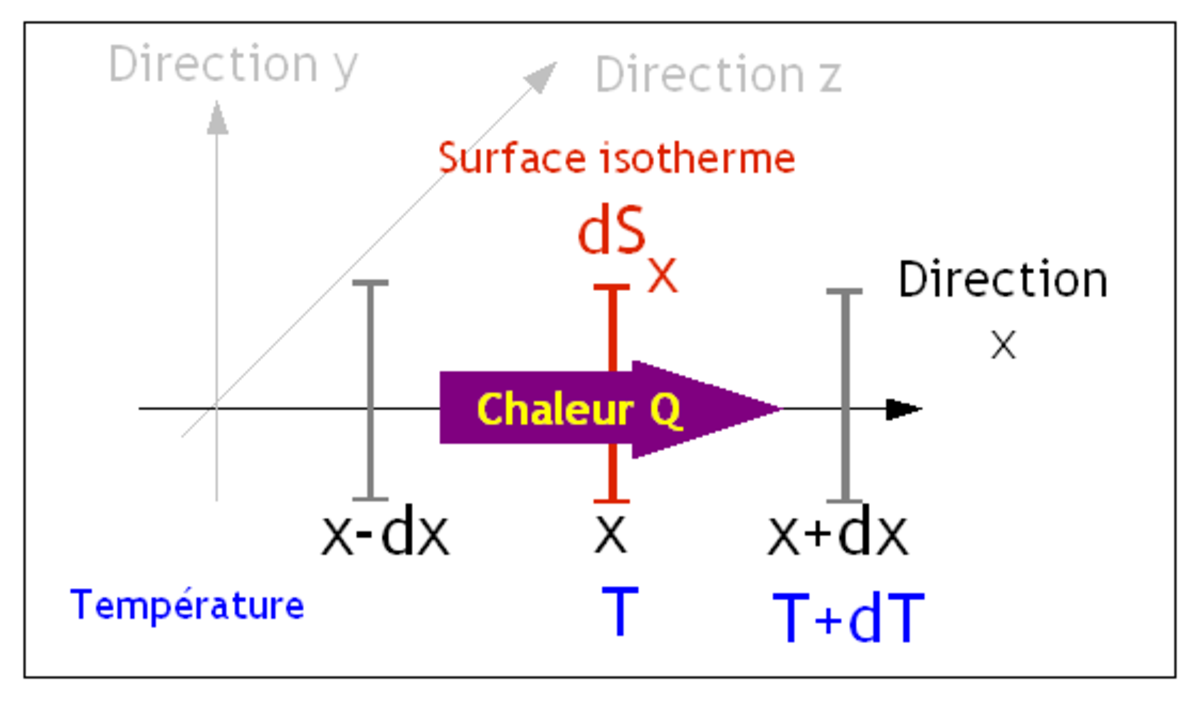
dans la direction (0,x) nous pouvons exprimer le transfert thermique selon x pendant un temps dt :

$dQ_x= - \lambda_x\ \frac{\delta T}{\delta x} dS_x dt\,$

Le flux thermique (à travers une surface élémentaire) est alors :

$d\Phi= \frac{dQ_x}{dt}= - \lambda_x \frac{\delta T}{\delta x} dS_x\,$

Nous pouvons en déduire la densité de flux :

$\varphi= \frac{d \Phi}{d S_x}\,$

$\varphi= - \lambda \frac{\delta T}{\delta x}\,$

Équation de la chaleur

Un bilan d'énergie, et l'expression de la loi de Fourier conduit à l'équation générale de conduction de la chaleur. Elle est ici donnée sous sa forme unidimensionnelle :

$\frac{\partial }{\partial x} \left (\lambda\,\frac{\partial T}{\partial x}\right) + P = \rho\,c\,\frac{\partial T}{\partial t}$ ,

où :

P est l'énergie produite au sein même du matériau en W.m^-3. Elle est souvent nulle (cas des dépôts de chaleur en surface de murs, par exemple), mais l'on peut citer de nombreux cas où elle ne l'est pas ; citons parmi d'autres l'étude du transfert de chaleur par conduction au sein du combustible nucléaire, ou l'absorption de la lumière ou des micro-ondes au sein des matériaux semi-transparents ...,
ρ est la masse volumique du matériau en kg.m^-3,
et c est la chaleur massique du matériau en J.kg^-1.K^-1.

(établissement de l'équation de conduction de la chaleur)

Au cas où P est nulle et où l'on fait de plus l'approximation que la conductivité thermique λ ne dépend pas de la position :

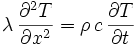
$\lambda\, \frac{\partial^2 T}{\partial x^2} = \rho\,c\,\frac{\partial T}{\partial t}$ .

Soit, en régime permanent (lorsque la température n'évolue plus avec le temps) :

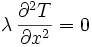
$\lambda\, \frac{\partial^2 T}{\partial x^2} = 0$ .

La solution de cette équation est alors :

T = A x + B

où A et B sont des constantes à fixer selon les conditions aux limites.

Conduction en régime stationnaire

Surface plane simple

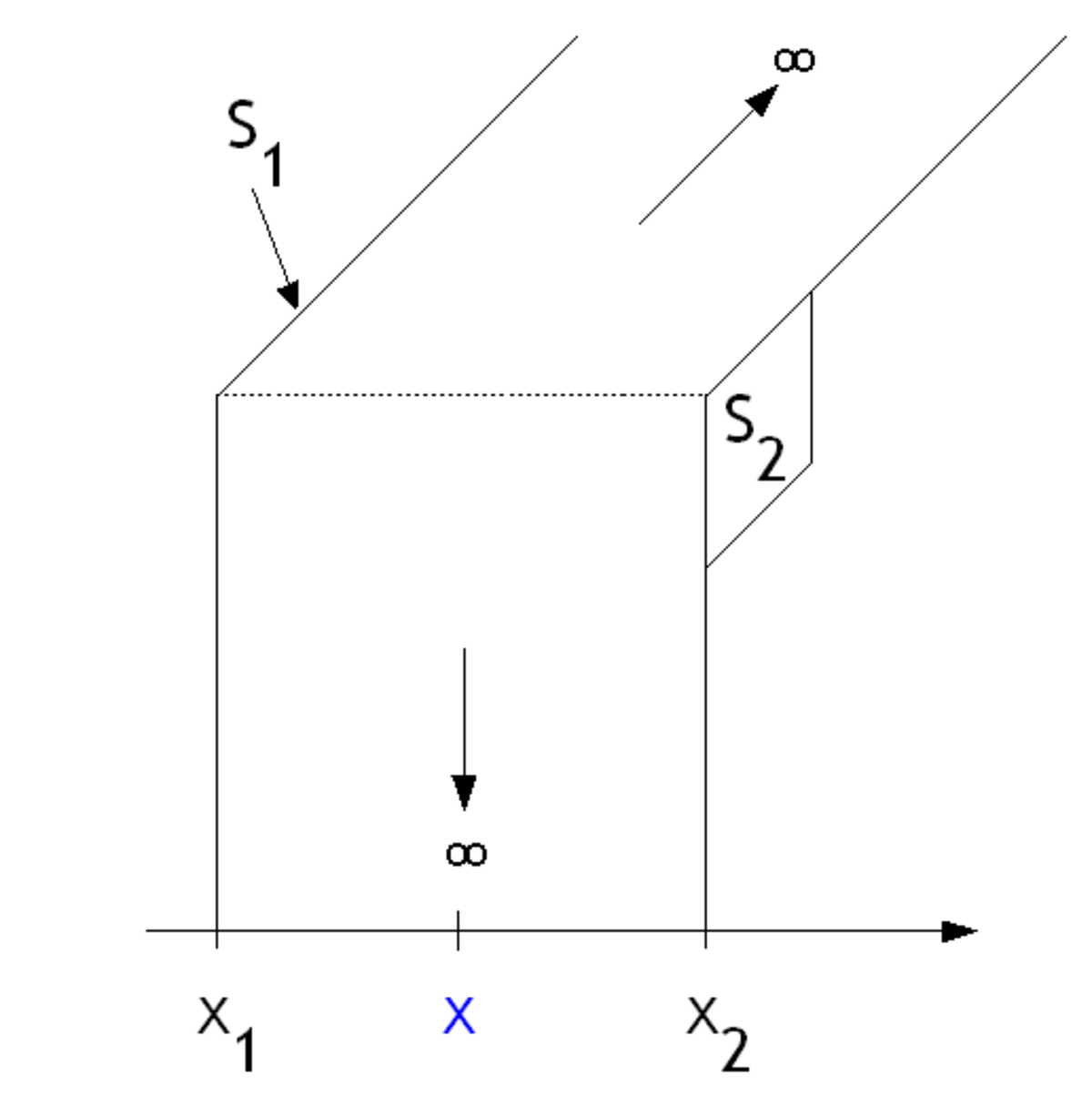
Le matériau est milieu conducteur thermiquement limité par deux plans parallèles (cas d'un mur). Chaque plan à une température T homogène sur toute sa surface. On considère que les plans ont des dimensions infinies pour s'affranchir des effets de bords. En conséquence le flux entrant est égal au flux sortant, il n'y a pas de pertes de chaleur sur les bords.

Le flux thermique s'écrit :

$\Phi = \frac{\lambda S}{e} (T_1-T_2)\,$

La densité de flux thermique surfacique s'écrit :

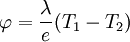
$\varphi= \frac{\lambda}{e} (T_1-T_2)$ .

Démonstration

Compte tenu de la définition :

$\frac{dT}{dx}= {\rm Constante}\,$ .

L'équation de Fourier devient

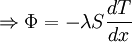
$\Rightarrow \Phi= - \lambda S \frac{dT}{dx}\,$ .

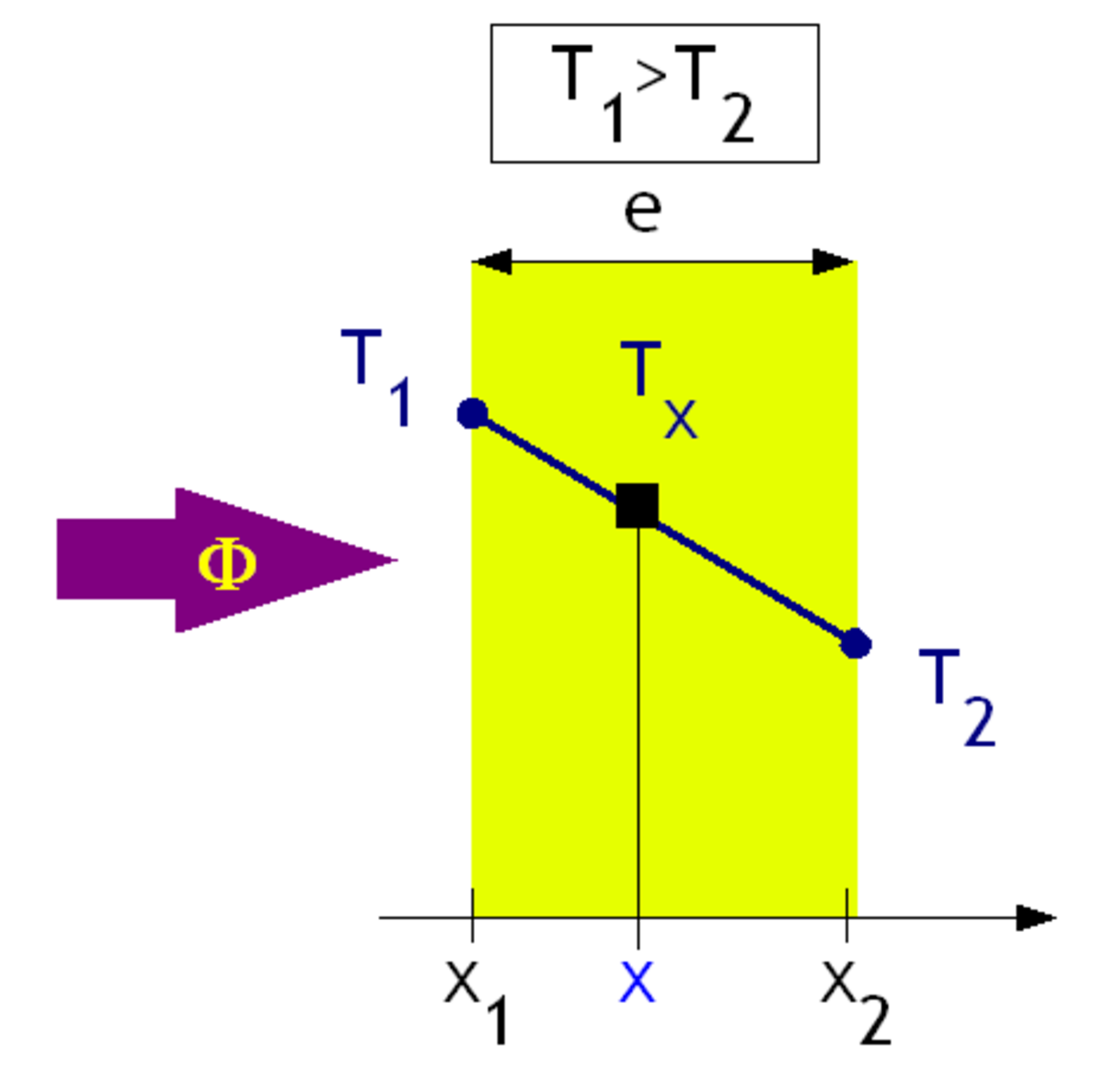
Profil de température dans un mur

Par intégration, il est possible de déterminer le profil de température dans l'épaisseur du mur

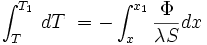
$\int_{T}^{T_1}\, dT\ = - \int_{x}^{x_1} \frac{\Phi}{\lambda S} dx\,$ ,

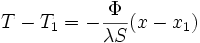
$T-T_1= - \frac{\Phi}{\lambda S} (x-x_1)\,$ ,

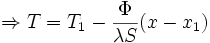
$\Rightarrow T= T_1 - \frac{\Phi}{\lambda S} (x-x_1)\,$ .

La variation de température dans un mur est donc linéaire.

Calcul du flux thermique.

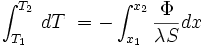
$\int_{T_1}^{T_2}\, dT\ = - \int_{x_1}^{x_2} \frac{\Phi}{\lambda S} dx\,$ ,

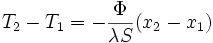
$T_2-T_1= - \frac{\Phi}{\lambda S} (x_2-x_1)\,$ ,

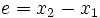
$e= x_2-x_1\,$ .

$\Rightarrow \Phi = \frac{\lambda S}{e} (T_1-T_2)\,$

Calcul de la densité de flux thermique surfacique.

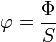
$\varphi= \frac{\Phi}{S}\,$ ,

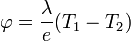
$\varphi= \frac{\lambda}{e} (T_1-T_2)\,$ .

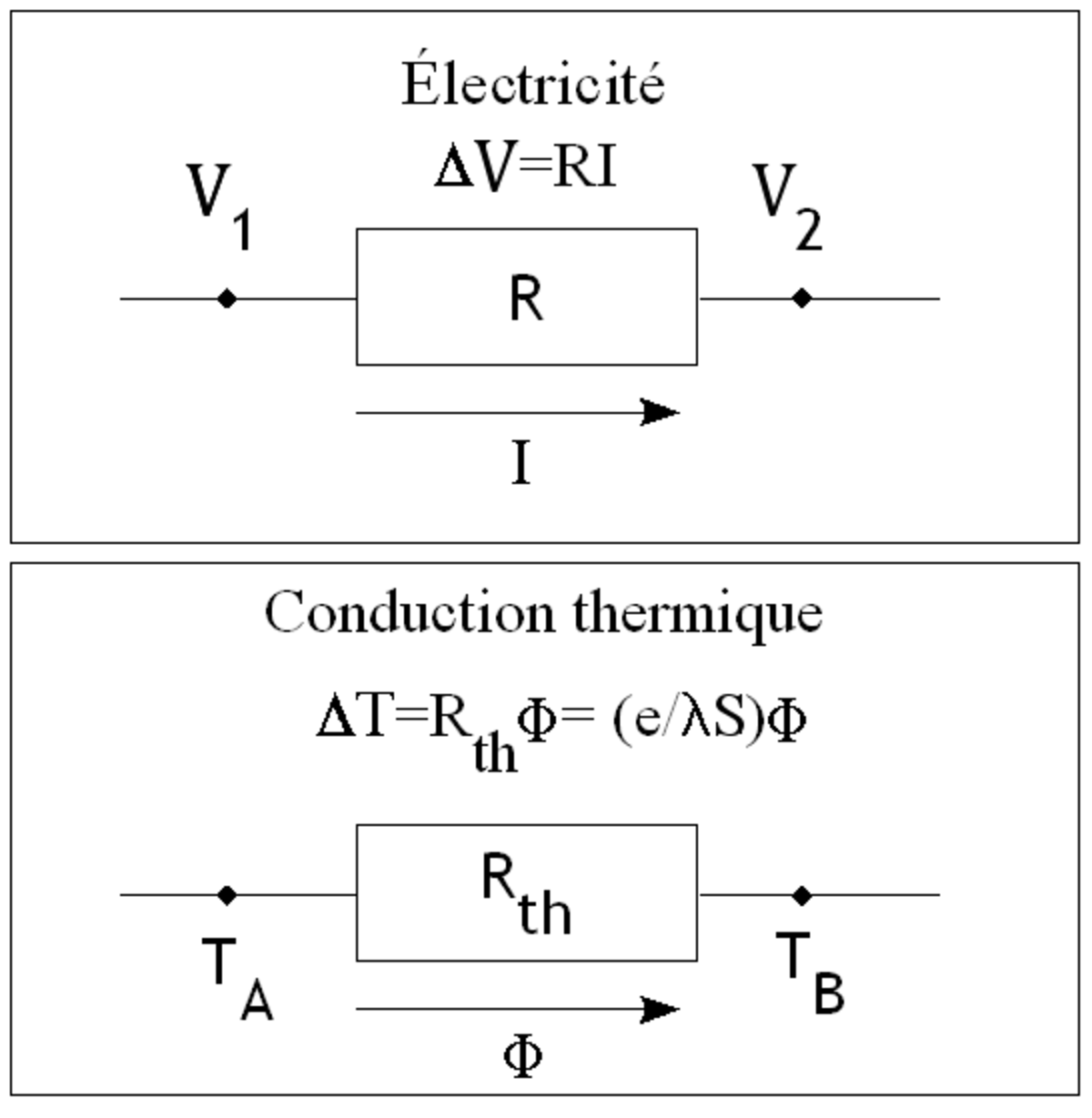
Analogie électrique

Par analogie avec l'électricité (loi d'Ohm) dans le cas particulier où la surface de contact entre chaque matériau est constante (flux surfacique $\varphi$ constant) nous pouvons mettre en parallèle les deux expressions :

$(U_1-U_2)= RI\,$

$(T_1-T_2)= \frac{e}{\lambda S} \Phi\,$

Nous pouvons mettre en parallèle la tension et l'intensité

$(U_1-U_2) \leftrightarrow (T_1-T_2),$

$I \leftrightarrow \Phi,$

Avec la résistance thermique

$R \leftrightarrow R_{thc}= \frac{e}{\lambda S}\,$

où $S$ est la surface du matériaux et $e$ son épaisseur. La résistance thermique $R t h c$ est homogène à des K.W^-1

Surfaces planes en série

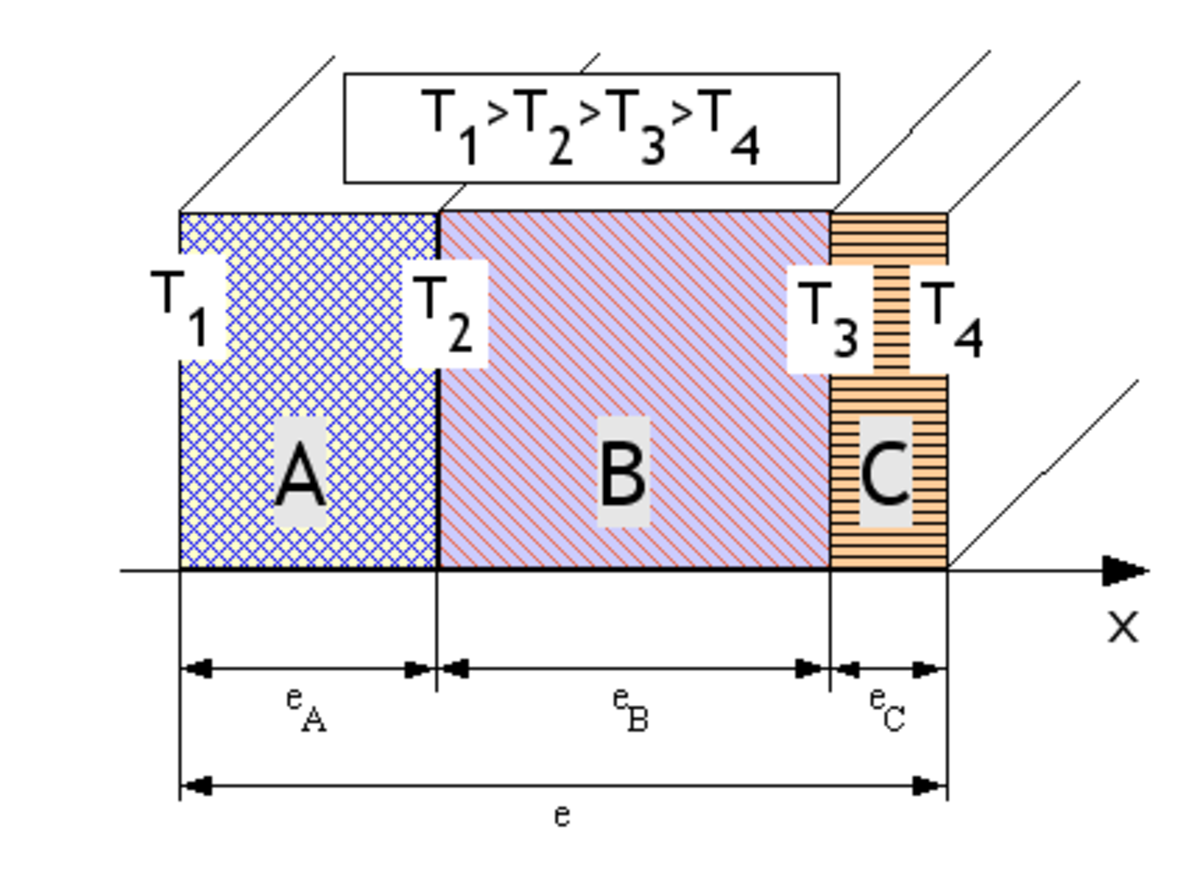
On considère des matériaux A B et C d'épaisseur respective $e A$ , $e B$ et $e C$ et de conductivité radiative respective $λ A$ , $λ B$ et $λ C$ .

Les hypothèses sont identiques à celles d'une surface plane simple. On considère que le contact entre chaque couche est parfait ce qui signifie que la température à l'interfaces entre 2 matériaux est identique dans chaque matériaux (Pas de saut de température au passage d'une interface).

Enfin la surface de contact entre chaque matériau est constante ce qui implique un flux surfacique $\varphi$ constant.

les résistances thermiques s'additionnent :

$T_1- T_4= (\frac{e_A}{\lambda_A S}+ \frac{e_B}{\lambda_B S}+ \frac{e_C}{\lambda_C S}) \Phi\ = (R_{thA}+ R_{thB}+ R_{thC}) \Phi$

Démonstration

Globalement, nous avons

$T_1- T_4= \frac{e}{\lambda S} \Phi\,$

Si l'on décompose

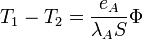
Pour la couche A : $T_1- T_2= \frac{e_A}{\lambda_A S} \Phi\,$

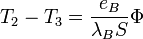
pour la couche B : $T_2- T_3= \frac{e_B}{\lambda_B S} \Phi\,$

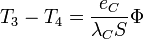
pour la couche C : $T_3- T_4= \frac{e_C}{\lambda_C S} \Phi\,$

Nota : Compte tenu des hypothèses, le flux (ou la densité de flux reste constant).

Avec :

$T_1- T_4= (T_1-T_2)+(T_2-T_3)+(T_3-T_4)\,$

Donc

$T_1- T_4= (\frac{e_A}{\lambda_A S}+ \frac{e_B}{\lambda_B S}+ \frac{e_C}{\lambda_C S}) \Phi\,$

$T_1- T_4= (R_{thA}+ R_{thB}+ R_{thC}) \Phi\,$

Le profil des températures
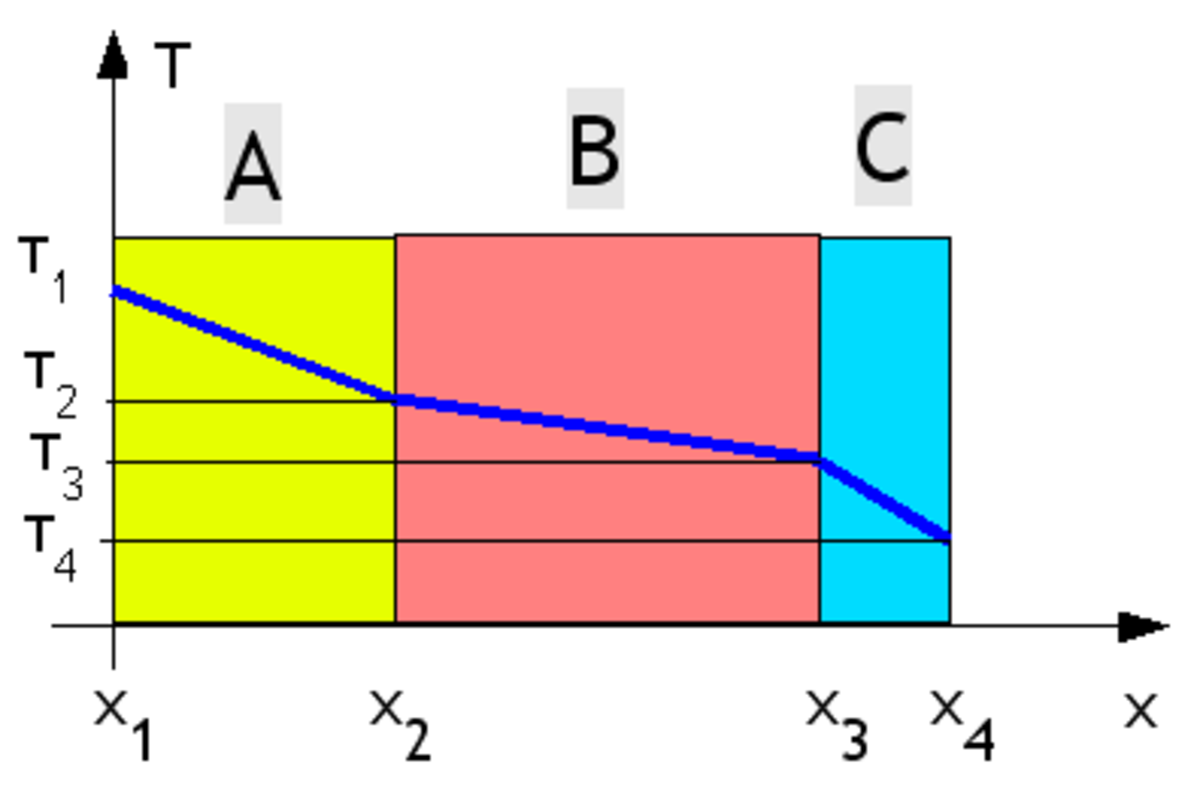
Pour chaque matériau la variation de température suit une loi du type :

$T= T_1- \frac{e_X}{\lambda_X S}\Phi\,$

La variation de température est donc linéaire dans l'épaisseur du matériau considéré. La pente dépend de λ (conductivité thermique) caractéristique de chaque matériau. Plus la conductivité thermique sera faible (donc plus le matériau sera isolant) plus la pente sera forte.

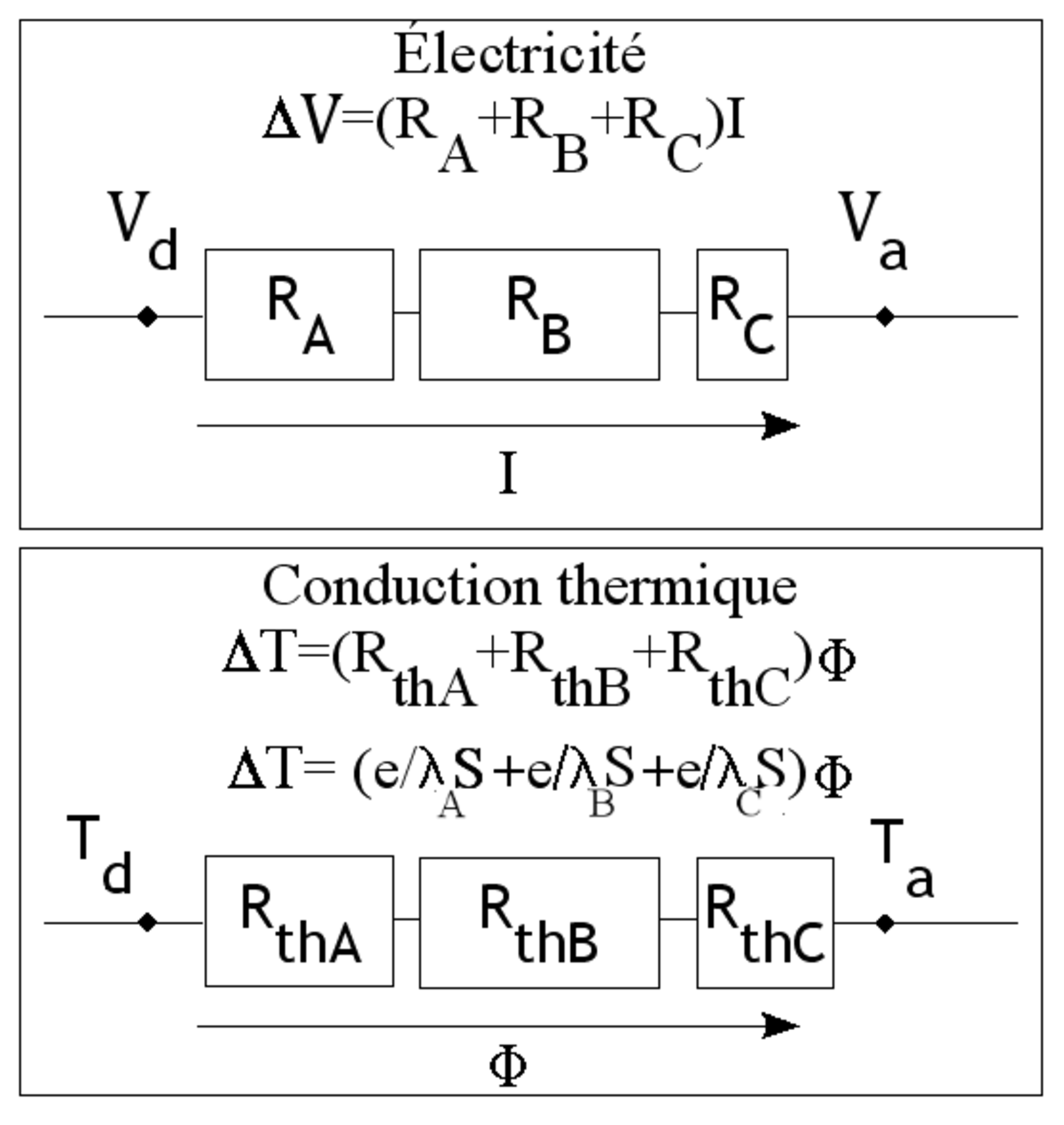
Analogie électrique
De la même manière que les résistances électriques en série s'additionnent, les résistances thermiques en série s'additionnent.

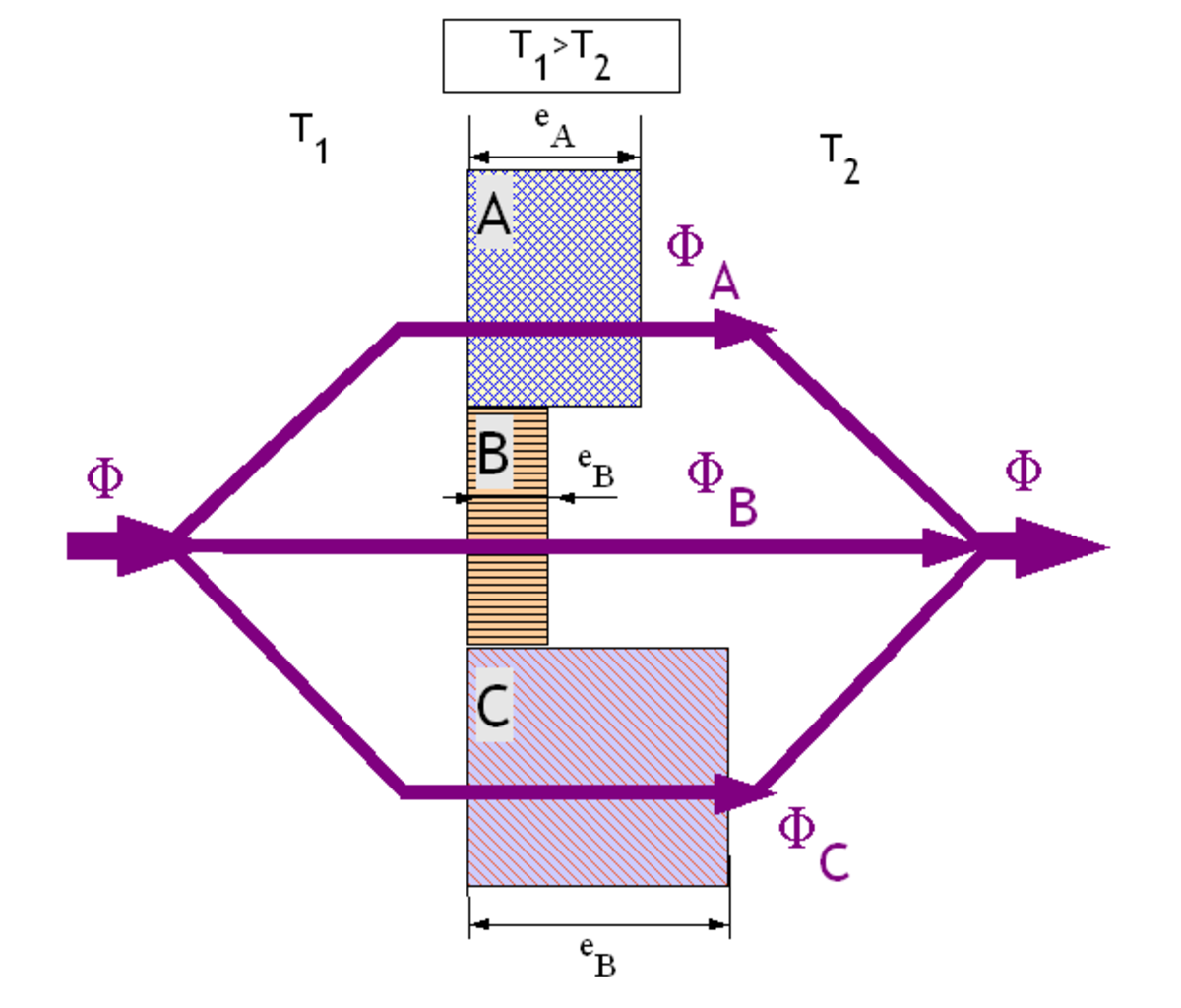
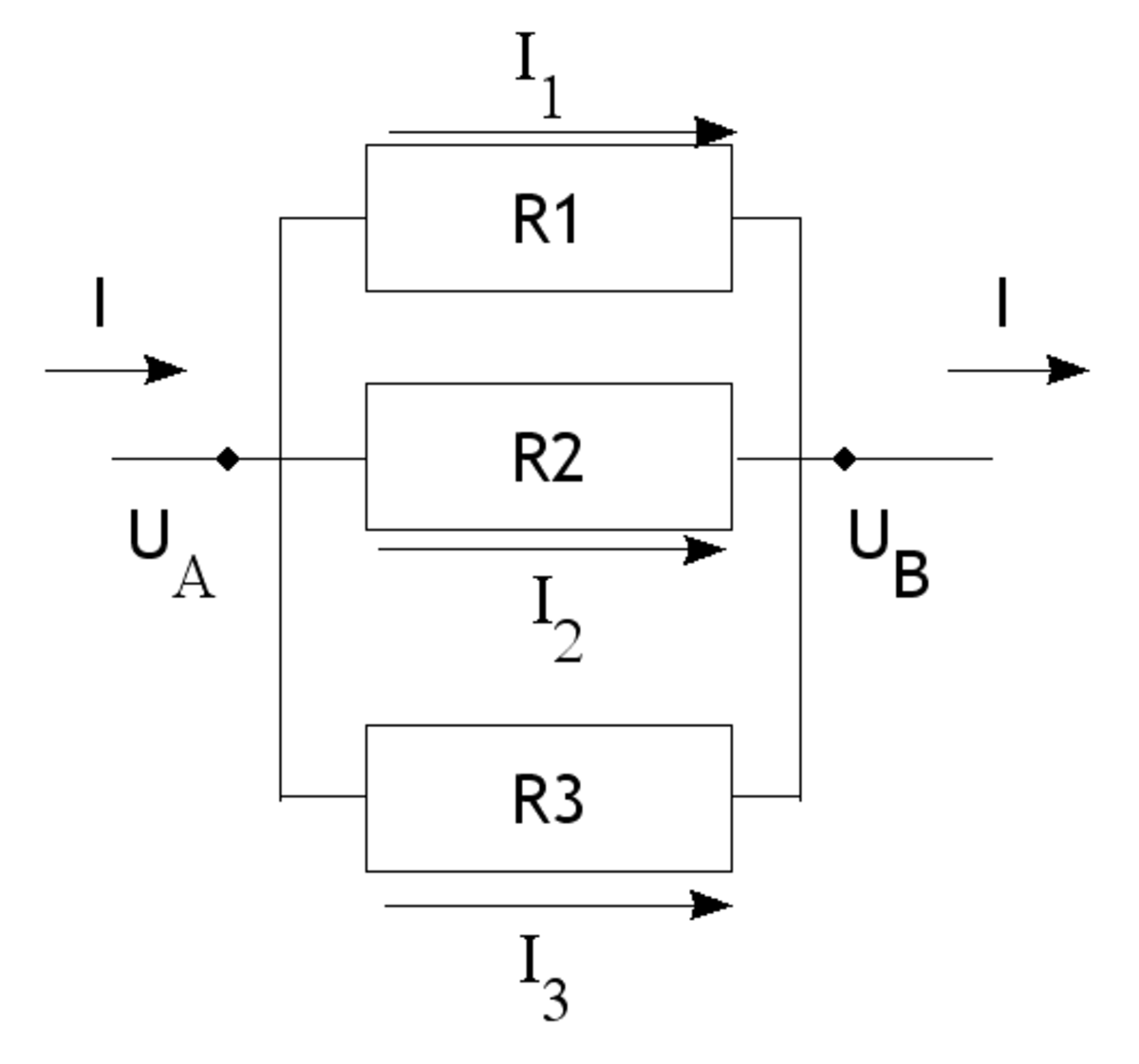
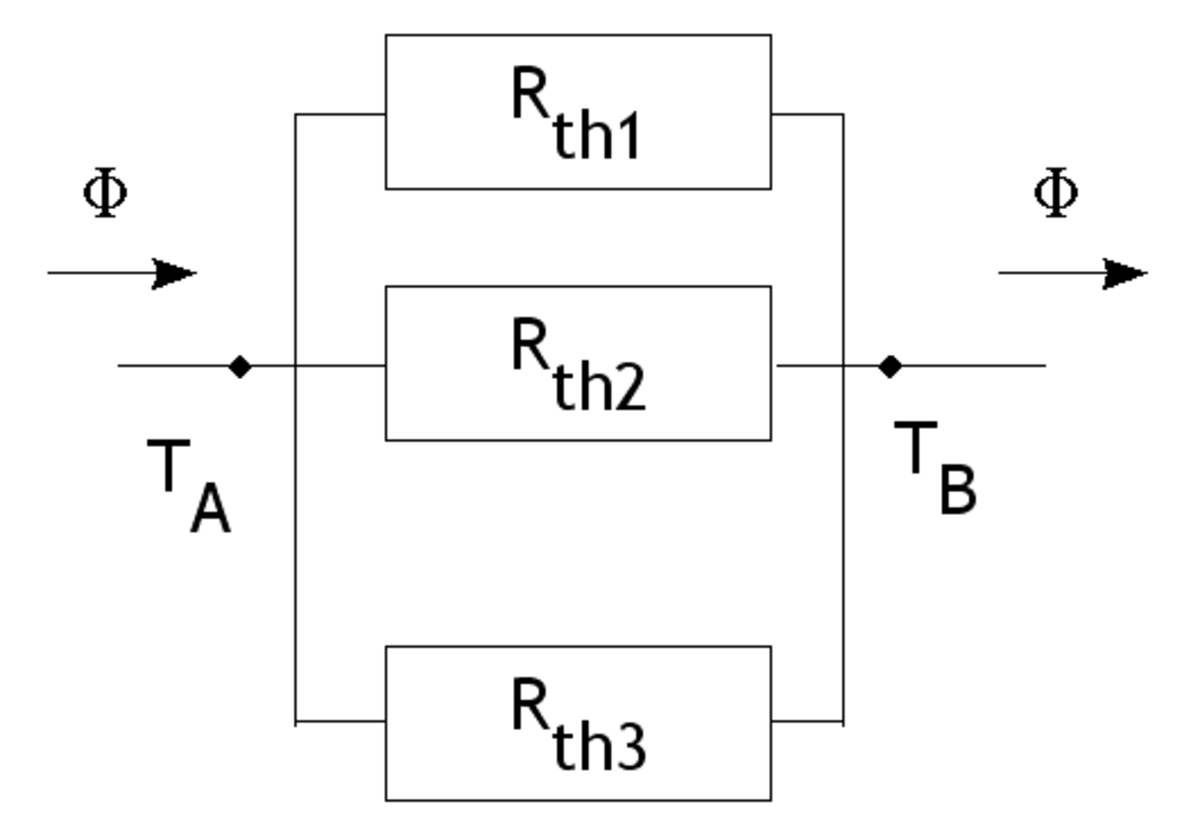
Surfaces planes en parallèle

On considère des matériaux plans juxtaposés côte à côte. Chaque matériau est homogène et limité par deux plans parallèles. C'est par exemple le cas d'un mur avec une fenêtre. Les hypothèses sont identiques à celles d'une surface plane simple. En supplément, on considère que la température est uniforme en surface de chaque élément (T₁ et T₂). Soit S_A, S_B et S_C les surfaces respectives des éléments A, B et C.

Par la suite, on fait l'hypothèse que le flux est toujours perpendiculaire à la paroi composée ; ceci n'est pas réaliste puisque la température de surface de chaque élément qui la composent est différente et qu'il existe par conséquent un gradient de température latéral (à l'origine des ponts thermiques). Aussi, il est nécessaire de corriger le flux de chaleur calculé dans la paroi composée à l'aide de coefficients de déperdition linéiques, spécifiques à chaque jonction de paroi (et pouvant être négligeables, cf. réglementation thermique TH 2000)

Les conductances thermiques s'additionnent :

$C_{th}= \frac{1}{R_{th}} = \frac{1}{\frac{e_A}{\lambda_A S_A}}+\frac{1}{\frac{e_B}{\lambda_B S_B}}+\frac{1}{\frac{e_C}{\lambda_C S_C}} = \frac{1}{R_{thA}} + \frac{1}{R_{thB}} + \frac{1}{R_{thC}}$

Démonstration

Pour chaque élément, le flux s'exprime suivant la relation

$T_1- T_2= \frac{e_X}{\lambda_X S} \Phi\,$

Avec en prenant l'analogie électrique

$R_X= \frac{e_X}{\lambda_X S_X}\,$

où $X$ est égale à $A$ , $B$ ou $C$ Nous avons donc

$\Phi_A= \frac{T_1- T_2}{R_A}\,$

$\Phi_B= \frac{T_1- T_2}{R_B}\,$

$\Phi_C= \frac{T_1- T_2}{R_C}\,$

Le flux total est égale à la somme des flux dans chaque élément

$\Phi= \Phi_A+ \Phi_B+ \Phi_C\,$

$\Phi= (T_1- T_2) (\frac{1}{R_A}+ \frac{1}{R_B}+ \frac{1}{R_C})\,$

Soit S la surface totale

$S= S_A+ S_B+ S_C\,$

Le flux surfacique s'écrit alors

$\varphi=\frac{\Phi}{S}\,$

Toujours par analogie avec les lois électriques, l'inverse de la résistance thermique est parfois appelé conductance thermique.

$C_{th}= \frac{1}{R_{th}} = \frac{1}{\frac{e_A}{\lambda_A S_A}}+\frac{1}{\frac{e_B}{\lambda_B S_B}}+\frac{1}{\frac{e_C}{\lambda_C S_C}} = \frac{1}{R_{thA}} + \frac{1}{R_{thB}} + \frac{1}{R_{thC}}$

Analogie électrique
Il est donc également possible de faire une analogie entre un montage électrique de résistances en parallèle.


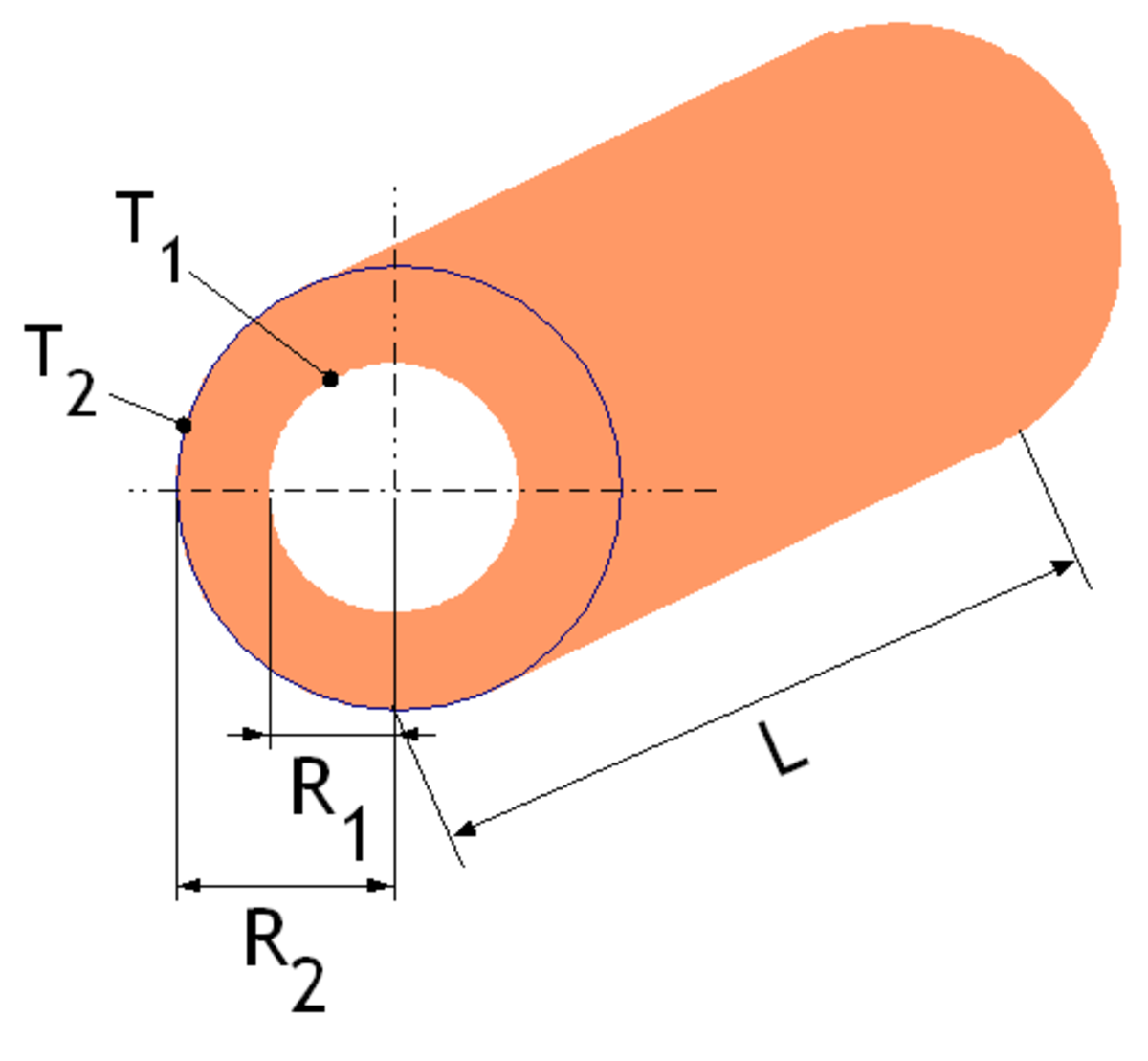
$I = (\frac{1}{R_1}+ \frac{1}{R_2}+ \frac{1}{R_3}) \Delta U\,$	$\Phi = (\frac{1}{R_{th1}}+ \frac{1}{R_{th2}}+ \frac{1}{R_{th3}}) \Delta T\,$

Surface cylindrique simple

Le tube simple est constitué d'un seul matériau homogène. La température est homogène sur chaque surface du tube. On considère que le tube à une longueur infinie afin de s'affranchir des effets de bord.

La variation de température s'écrit :

$\ T_1-T_2= \frac{\Phi}{2 \pi \lambda L } \ln \frac{R_2}{R_1}$

Démonstration

Si l'on considère une variation dR à l'intérieur du matériau constituant le tube, la loi de Fourier s'exprime alors :

$\Rightarrow \Phi= - \lambda S \frac{dT}{dR}\,$

Variation de la température dans l'épaisseur du tube

Textérieure">

Évolution de la température dans l'épaisseur d'un tube simple avec T_intérieure>T_extérieure

Soit S la surface d'un cylindre :

$S= 2 \pi R L\,$

Nous pouvons écrire la loi de Fourier sous la forme :

$\Phi= - \lambda 2 \pi R L \frac{dT}{dR}\,$

$\frac{dR}{R}= - \frac{2 \pi \lambda L dT}{\Phi}\,$

$\int_{R_1}^{R} \frac{dR}{R}= - \frac{2 \pi \lambda L }{\Phi} \int_{T_1}^{T} dT\,$

$\ln \frac{R}{R_1}= \frac{2 \pi \lambda L }{\Phi} (T_1-T)\,$

La variation de température dans le matériau est donc

$\ T= T_1 - \frac{\Phi}{2 \pi \lambda L } \ln \frac{R}{R_1}\,$

Sur la totalité de l'épaisseur du tube, la variation est

$\ T_1-T_2= \frac{\Phi}{2 \pi \lambda L } \ln \frac{R_2}{R_1}\,$

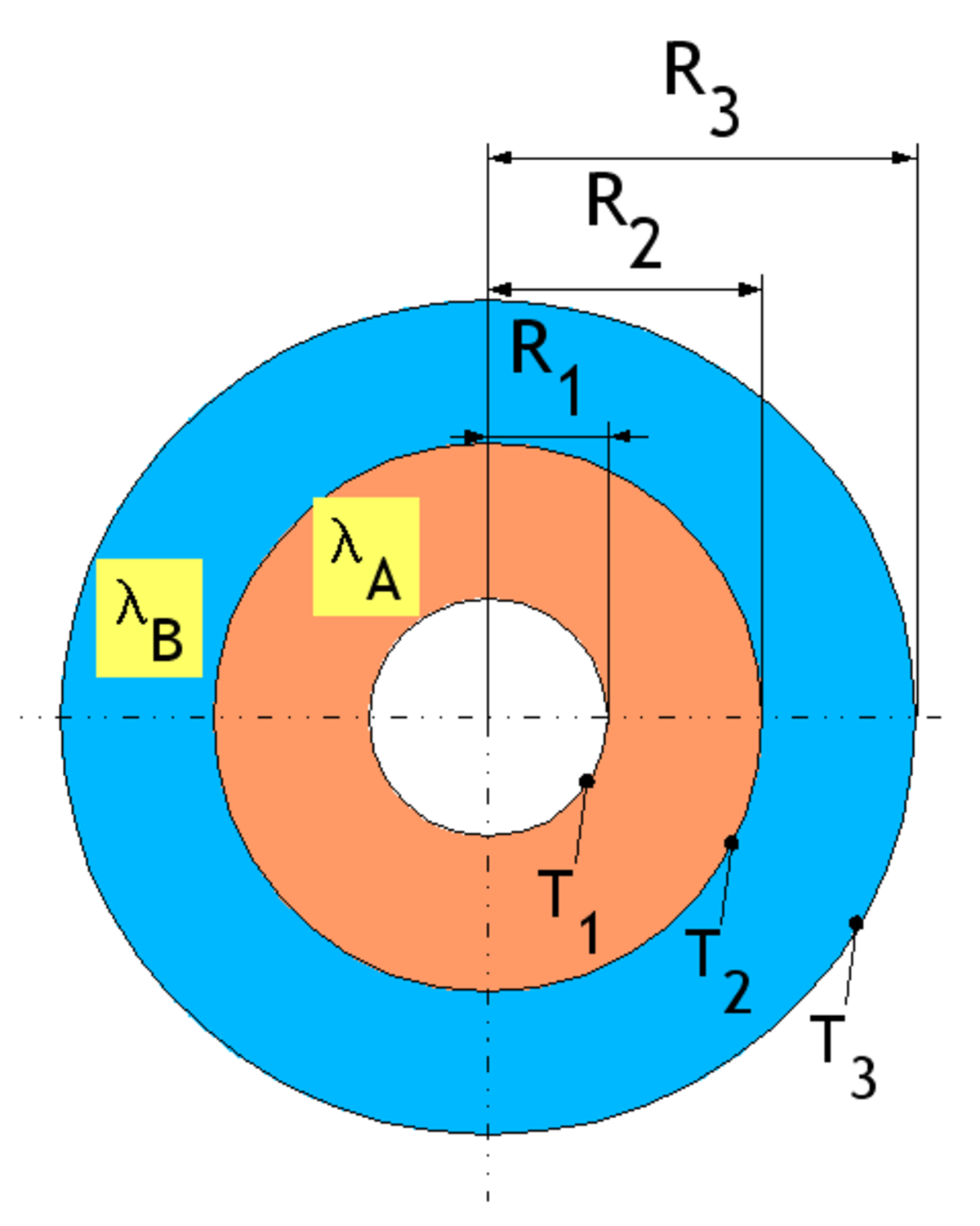
Surfaces cylindriques concentriques

Schéma d'un tube concentrique

Le tube concentrique est constitué de tubes disposés en couches concentriques. On considère que le contact est parfait entre les tubes. La température est homogène sur chaque surface du tube. On considère que le tube à une longueur L infinie afin de s'affranchir des effets de bord.

La résistance totale du tube s'exprime suivant une loi de type " série " comme le mur composé série :

$\ R_{thT}= R_{thA} + R_{thB}$

Démonstration

Évolution de la température dans la première couche :

$\ T_1-T_2= \frac{\Phi}{2 \pi \lambda_A L } \ln \frac{R_2}{R_1}\,$

Évolution de la température dans la deuxième couche :

$\ T_2-T_3= \frac{\Phi}{2 \pi \lambda_B L } \ln \frac{R_3}{R_2}\,$

Sur la totalité de l'épaisseur du tube :

$\ T_1-T_3= \frac{\Phi}{2 \pi L } \left ( \frac {\ln \frac {R_2}{R_1} }{\lambda_A} + \frac {\ln \frac {R_3}{R_2} }{\lambda_B}\right )\,$

La résistance thermique de la couche A

$\ R_{thA}= \frac {\ln \frac {R_2}{R_1} }{\lambda_A}\,$

La résistance thermique de la couche B

$\ R_{thB}= \frac {\ln \frac {R_3}{R_2} }{\lambda_B}\,$

La résistance totale du tube s'exprime suivant une loi de type " série " comme le mur composé série :

$\ R_{thT}= R_{thA} + R_{thB}\,$

Conduction en régime dynamique

Notes

D'où vient cette structure fractale observée dans une bactérie ?

Il y a 6 heures

Découverte majeure dans les allergies respiratoires

Il y a 6 heures

Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers

Il y a 11 heures

Propagation inquiétante de la "mouche noire" suceuse de sang en Allemagne

Il y a 11 heures

Le hasard confère le prix Turing et 1 million de dollars au mathématicien Avi Wigderson

Il y a 13 heures

AI Act: comment encadrer l'intelligence artificielle en Europe ?

Il y a 13 heures

Quelle est cette forme étrange photographiée près de la Lune ?

Il y a 1 jour

Si vous avez déjà eu une entorse de la cheville, attention à ceci

Il y a 1 jour

Démonstration d'une nouvelle technologie de lévitation, stable et sans supraconductivité

Il y a 1 jour

Ces indices d'une rupture imminente de la faille de San Andreas

Il y a 1 jour

Cet effet inattendu de la musculation sur la mémoire

Il y a 1 jour

Les géantes Uranus et Neptune ne seraient pas faites comme nous l'imaginions

Il y a 1 jour

Parker Solar Probe se prépare à battre le record de vitesse de l'humanité

Il y a 2 jours

Nos ancêtres à l'époque des dinosaures

Il y a 2 jours

Observer directement le Big Bang avec un télescope plus puissant que le James Webb ?

Il y a 2 jours

Découverte de 17 variants génétiques liés à la maladie d'Alzheimer

Il y a 2 jours

Un immense glacier du Groenland est littéralement en train de fondre sous nos yeux

Il y a 2 jours

Découverte: des bactéries anticholestérol dans notre intestin

Il y a 2 jours

Des dinosaures aux oiseaux: cette anomalie de l'ADN a trompé les scientifiques

Il y a 3 jours

De la vie cachée 800 mètres sous terre: comment est-ce possible ?

Il y a 3 jours

Analyse d'un signal radio inhabituel, en provenance de cet objet spatial extrême

Il y a 3 jours

Ce liquide est programmable, pouvant changer de consistance et de couleur

Il y a 3 jours

Un trou noir trop léger, ou une étoile à neutrons trop lourde ? L'objet qui intrigue les scientifiques

Il y a 3 jours

Un lien démontré entre vapotage, petit-déjeuner et maux de tête

Il y a 3 jours

Un immense "arc-en-ciel" détecté sur une exoplanète

Il y a 4 jours

Des scientifiques étudient 40 ans de vie marine dans... des conserves de saumon

Il y a 4 jours

Cette innovation va améliorer significativement la sensibilité des détecteurs d'ondes gravitationnelles

Il y a 4 jours

Découverte d'une ingénierie humaine vieille de... 300 000 ans

Il y a 4 jours

Psyche: une mission à la découverte de ce très mystérieux objet spatial

Il y a 5 jours

Peur généralisée: des scientifiques découvrent comment ne pas être tétanisé par la peur

Il y a 5 jours

Découverte accidentelle d'une mémoire quantique au potentiel énorme

Il y a 5 jours

Des chercheurs ont créé artificiellement des "minifoies"

Il y a 5 jours

Surprise: la surface lunaire a "coulé" sous la croûte

Il y a 6 jours

Un curieux "point de bascule" découvert dans l'évolution des champignons

Il y a 6 jours

Des humains préhistoriques ont gravé ces traces de dinosaures

Il y a 6 jours

Ralentissement significatif d'importants courants océaniques: des répercussions graves ?

Il y a 6 jours

Les étoiles à neutrons, des aspirateurs de matière noire ?

Il y a 6 jours

Greffer de la peau de porc pour soigner les plaies

Il y a 6 jours

Le secret d'une jeunesse éternelle à proximité du trou noir de notre Voie Lactée

Il y a 7 jours

Une quantité phénoménale de volcans cachés sous l'Antarctique: des risques d'éruption ?

Il y a 7 jours

Une mission spatiale dans l'espace interstellaire, à 1000 unités astronomiques ?

Il y a 7 jours

Ce régime montre une efficacité contre la maladie d'Alzheimer

Il y a 7 jours

Les dinosaures contredisent ce principe scientifique

Il y a 7 jours

Sentons-nous le goût des aliments uniquement avec notre langue ?

Il y a 7 jours

Nova: une rare et impressionnante explosion stellaire bientôt visible dans le ciel

Il y a 8 jours

Découverte d'une importante vertu anti-vieillissement à cette vitamine

Il y a 8 jours

Quand le cerveau ne perçoit que des visages distordus: la prosopométamorphopsie

Il y a 8 jours

La future station lunaire Gateway sous le feu des radiations spatiales

Il y a 8 jours

Cette découverte pourrait améliorer considérablement l'efficacité des traitements contre le cancer

Il y a 8 jours

Les orages violents en France sont déjà intensifiés par le changement climatique

Il y a 8 jours

Populaires

Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers

Parker Solar Probe se prépare à battre le record de vitesse de l'humanité

Ces indices d'une rupture imminente de la faille de San Andreas

Découverte majeure dans les allergies respiratoires

D'où vient cette structure fractale observée dans une bactérie ?

De la vie cachée 800 mètres sous terre: comment est-ce possible ?

Toutes les ventes flash et Codes Promos Amazon

Cdiscount: les meilleures réductions actuelles

Page générée en 0.011 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise