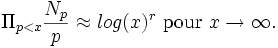Conjecture de Birch et Swinnerton-Dyer - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En mathématiques, la conjecture de Birch et Swinnerton-Dyer relie le rang du groupe abélien de points sur un corps de nombres d'une courbe elliptique E à l'ordre du zéro de la fonction L associée L(E,s) pour s = 1.

Ouverte de puis plus de quarante ans, la conjecture n'a été prouvée que dans des cas particuliers. Largement reconnue comme un des problèmes mathématiques les plus difficiles et les plus profonds encore ouverts à la fin du XX^e siècle, elle est un des sept problèmes du prix du millénaire pour lesquels le Clay Mathematics Institute offre un prix d'un million de dollars US.

Arrière-plan

En 1922 Louis Mordell a démontré que le groupe de points rationnels d'une courbe elliptique possède une base finie. Ce qui signifie que pour toute courbe elliptique, il existe un sous-ensemble fini de points rationnels sur la courbe à partir desquels tous les autres points peuvent être générés.

Si le nombre de points rationnels sur une courbe est infini alors certains points dans une base finie doive être d'ordre infini. Le nombre de points de la base d'ordre infini est appelé le rang de la courbe, et est une importante propriété invariante d'une courbe elliptique.

Si le rang d'une courbe elliptique est 0 alors la courbe possède seulement un nombre fini de points rationnels. D'un autre côté, si le rang de la courbe est plus grand que 0, alors la courbe possède un nombre infini de points rationnels.

Bien que le théorème de Mordell montre que le rang d'une courbe elliptique est toujours fini, il ne donne pas de méthode efficiente pour calculer le rang de chaque courbe. Le rang de certaines courbes elliptiques peut être calculé en utilisant des méthodes numériques mais celles-ci ne peuvent pas être généralisées pour toutes les courbes.

Une fontion L L(E,s) peut être définie pour une courbe elliptique E en construisant un produit eulérien à partir du nombre de points sur la courbe modulo chaque nombre premier p. Cette fonction L est analogue à la fonction Zeta de Riemann et aux séries L de Dirichlet qui est définie pour une forme quadratique binaire.

La définition naturelle de L(E,s) converge seulement pour les valeurs de s dans le plan complexe avec Re(s) > 3/2. Helmut Hasse a conjecturé que L(E,s) pouvait être étendue par prolongement analytique au plan complexe entier. Cette conjecture fut démontrée en premier par Max Deuring pour les courbes elliptiques avec la multiplication complexe. Elle fut montrée vraie ultérieurement pour toutes les courbes elliptiques, comme une conséquence du théorème de Taniyama-Shimura.

Trouver des points rationnels sur une courbe elliptique générale est un problème difficile. Trouver les points sur une courbe elliptique modulo un nombre premier donné p est conceptuellement direct, puisqu'il n'existe seulement qu'un nombre fini de possibilités de vérification. Néanmoins, pour des grands nombres premiers, cela requiert des calculs intensifs.

Histoire

Au début des années 1960, Bryan Birch et Peter Swinnerton-Dyer ont utilisé l'ordinateur EDSAC au laboratoire informatique de l'Université de Cambridge pour calculer le nombre de points modulo p (désigné par N_p) pour un grand nombre de nombres premiers p sur des courbes elliptiques dont le rang était connu. À partir de ces résultats numériques, ils émirent la conjecture que N_p pour une courbe E avec un rang r obéissent à la loi asymptotique

Initialement, ceci était basé sur quelque chose de ténu montré par des points graphiques qui ont induit un certain scepticisme chez le maître de Birch, J. W. S. Cassels.

Ceci les conduisit à faire une conjecture à propos du comportement de la fonction L d'une courbe elliptique L(E,s) en s = 1, expressément, qu'il y aurait un zéro d'ordre r en ce point. Ceci fut une conjecture particulièrement spectaculaire car à cette époque, le prolongement analytique de L(E,s) au point s = 1 était seulement établi pour les courbes avec multiplication complexe.

La conjecture fut par la suite étendue pour inclure la prédiction du résidu du zéro en s = 1 en fonction d'invariants de la courbe étudiés par Cassels, Tate, Shafarevich et d'autres.

Par exemple, considérons un polynôme en deux variables $f (x, y)$ non-nul dont les coefficients sont des nombres rationnels. Supposons que la courbe projective plane associée n'ait pas de singularités. Intéressons-nous aux solutions de l'équation $f (x, y) = 0$ en des nombres rationnels (x,y). Alors,

Si le degré de f est égal à 1 ou 2 (le cas d'une droite ou d'une conique) soit cet ensemble est vide (par exemple $f (x, y) = x 2 + y 2 + 1$ ) soit il est infini, auquel cas la courbe projective associée est isomorphe à une droite projective.
Si le degré de f est supérieur ou égal à 4 alors Gerd Faltings a démontré que cet ensemble est fini (conjecture de Mordell).
Si le degré de f est égal à 3 tous les cas sont possibles. Si cet ensemble est non-vide la courbe projective associée est une courbe elliptique. La conjecture de Birch et Swinnerton-Dyer prédit alors la " taille " (le rang) de l'ensemble des solutions en fonction du prolongement méromorphe d'une série génératrice formée à partir du nombre de solutions de f(x,y)=0 modulo p pour tout nombre premier p. Elle prédit en particulier le fait de savoir si cet ensemble est fini ou infini.

Enoncé plus précis

Considérons une courbe elliptique sur $\mathbb{Q}$ . La conjecture de Birch et Swinnerton-Dyer prédit que l'ordre d'annulation de la fonction L de cette courbe elliptique en s=1 est égal au rang de cette même courbe. Elle prédit même la valeur du premier terme non-nul dans le développement limité en s=1 de cette fonction L.

État actuel

La conjecture de Birch et Swinnerton-Dyer a été démontrée seulement dans les cas particuliers suivants :-

En 1976, John Coates et Andrew Wiles ont démontré que si E est une courbe avec la multiplication complexe et L(E,1) n'est pas 0 alors E possède seulement une nombre fini de points rationnels, dans le cas de nombre de classe 1. Ceci fut étendu à tous les corps quadratiques imaginaires par Nicole Artaud.
En 1983, B. Gross et D. Zagier ont montré que si une courbe elliptique modulaire possède un zéro de premier ordre à s = 1 alors elle possède un point rationnel d'ordre infini.
En 1990, Victor Kolyvagin a montré qu'une courbe elliptique modulaire E pour laquelle L(E,1) n'est pas zéro est de rang 0, et une courbe elliptique modulaire E pour laquelle L(E,1) possède une zéro de premier ordre à s = 1 est de rang 1.
En 1999, Andrew Wiles, Christophe Breuil, Brian Conrad, Fred Diamond et Richard Taylor ont démontré que toutes les courbes elliptiques sont modulaires (le théorème de Taniyama-Shimura), qui étend les deux résultats précédents à toutes les courbes elliptiques.

Rien n'a été démontré pour les courbes de rang plus grand que 1, bien qu'il existe une importante évidence numérique pour la véracité de la conjecture.

La conjecture de Birch et Swinnerton-Dyer est un des sept Problèmes du prix du millénaire sélectionnés en mai 2000 par le Clay Mathematics Institute, qui offre un prix d'un million de dollars US pour une preuve de la conjecture entière.