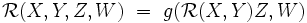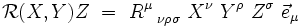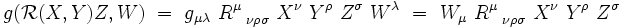Courbure - Définition

Courbure d'une surface de R3

Pour disposer de versions algébrisées de toutes les notions de courbure introduites, il convient de considérer une surface orientée.

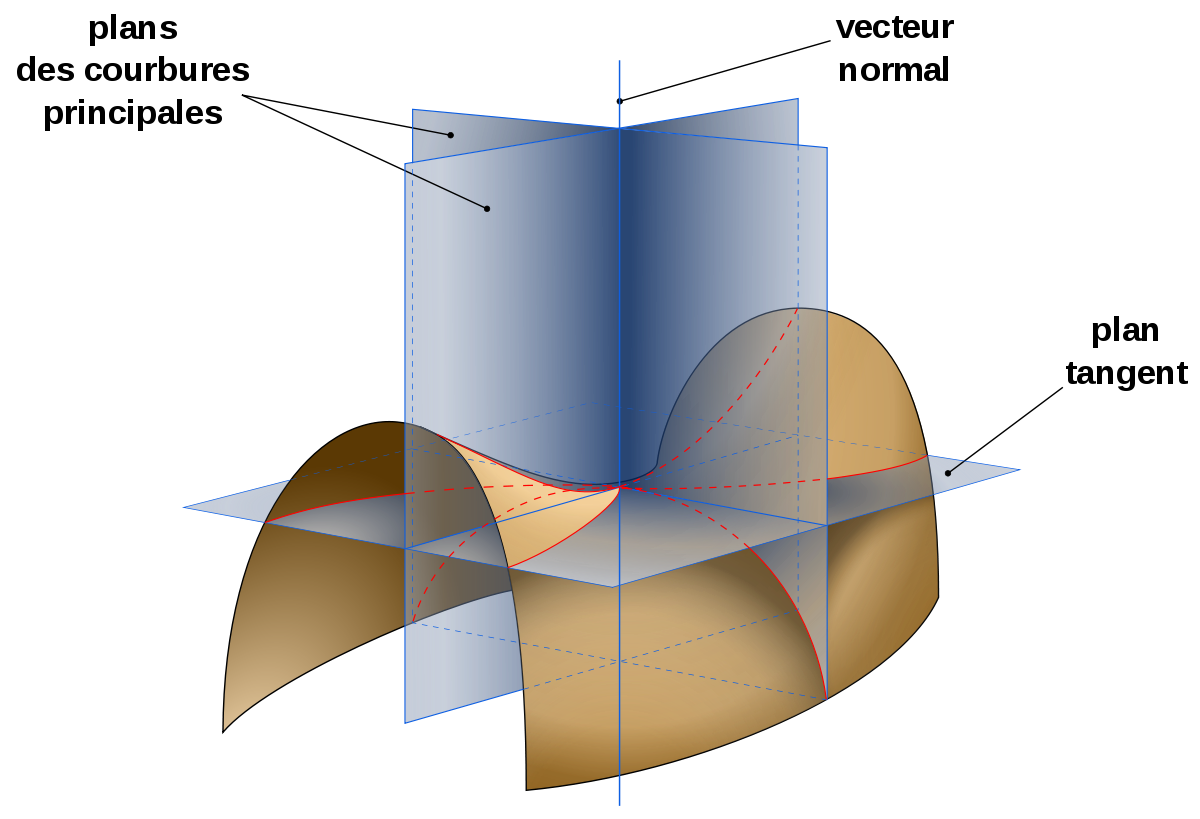
Courbures principales

En un point M de la surface, on considère un plan tournant, perpendiculaire en M au plan tangent à la surface. Ce plan intersecte la surface considérée en une courbe. À chacune des courbes ainsi construite est associée sa courbure en M.

Les valeurs minimum et maximum de la courbure portent le nom de courbures principales. En général, elles sont différentes et, dans ce cas, les plans correspondant aux deux courbures principales sont perpendiculaires entre eux. Leur intersection avec le plan tangent définit les directions principales.

Courbures principales et directions principales sont respectivement les valeurs propres et vecteurs propres d'un endomorphisme symétrique du plan tangent. Ce dernier, l'endomorphisme de Weingarten, s'obtient à partir de la différentielle de l'application de Gauss.

Courbure moyenne

On appelle courbure moyenne la moyenne des courbures principales, soit

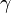
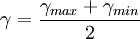
Il s'agit de la trace de l'endomorphisme de Weingarten.

Courbure de Gauss

On appelle courbure de Gauss le produit des courbures principales, soit

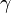
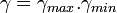
Il s'agit du déterminant de l'endomorphisme de Weingarten.

Courbure totale

La courbure totale d'une surface orientée S de l'espace est l'intégrale de la courbure de Gauss sur la surface. Elle s'interprète également comme l'aire (algébrique) balayée par le vecteur normal unitaire sur la sphère unité.

Définition de la courbure d'un arc plan

La courbure est définie comme la norme du vecteur accélération d'un mobile parcourant une courbe à vitesse constante égale à 1. En d'autres termes, c'est la dérivée seconde par rapport à l'abscisse curviligne de la position du mobile.

En pratique si on considère une courbe paramétrée , la courbure est la norme du vecteur , où s est l'abscisse curviligne définie par , où on note et .

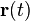
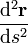
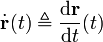
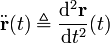
Le problème revient donc à calculer :

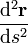
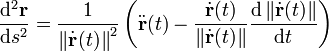
On peut également écrire cette formule ainsi:

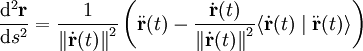
où désigne le produit scalaire entre un vecteur et un vecteur .

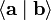
Calcul explicite

Pour une courbe plane en coordonnées paramétriques dans un repère orthonormé , la courbure s'exprime par

.

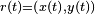
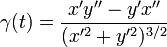
Dans le cas où la courbe est paramétrée par l'abscisse cartésienne la courbure s'exprime par

.

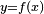
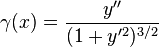
Lorsque l'équation de la courbe est exprimée en coordonnées polaires, , sa courbure se calcule par la formule

,

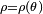
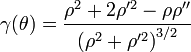
dans laquelle la dérivée est prise par rapport à .

Courbure d'une variété riemanienne

En géométrie riemannienne, la courbure est un tenseur introduit à partir de la notion de connexion. Cet objet s'est dégagé comme le plus pertinent, mais il peut être difficile à appréhender en raison du formalisme nécessaire à son introduction. La courbure sectionnelle d'une variété riemannienne, d'abord plus simple, véhicule autant d'information que le tenseur de courbure, et permet de faire le lien avec la courbure de Gauss.

Courbure sectionnelle

On définit une courbure sectionnelle pour chacun des 2-plans inclus dans chacun des espaces tangents d'une variété riemannienne. Si P est un tel plan en un point m, on considère en premier lieu la famille des géodésiques issues de m selon les vecteurs de P. Cette famille constitue une surface paramétrée incluse dans la variété, image du 2-plan par l'application exponentielle.

La courbure sectionnelle du 2-plan est alors la courbure de Gauss de cette surface. Formellement, la collection de toutes les courbures sectionnelles constitue une application sur la grassmannienne des 2-plans, à valeurs réelles.

Définition du tenseur de courbure

Soit une variété affine M de dimension n, c'est-à-dire une variété munie d'une connexion affine . À partir de cette connexion, on définit le tenseur de courbure, ou tenseur de Riemann . Ce tenseur est défini pour X, Y et Z champs de vecteurs sur la variété par :

,

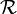
où [X, Y] est le crochet de Lie de X et Y. est un champ d'endomorphisme de l'espace fibré tangent TM : à tout champ de vecteur Z, il associe un nouveau champ de vecteur noté R(X, Y)Z.

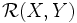
Introduction d'une métrique

On munit la variété affine M d'un tenseur métrique g : (M,g) est alors une variété riemannienne, et on peut définir une courbure à valeurs réelles par :

.

En composantes dans une base locale , est le vecteur qui s'écrit :

.

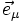
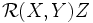
où les sont les composantes du tenseur de courbure. On a alors :

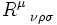
En prenant sa trace (par rapport à X et Y), on obtient le tenseur de courbure de Ricci, et en prenant la trace de celui-ci, on obtient la courbure scalaire (qui est une fonction de M dans ).

Courbure de Ricci

Courbure scalaire

Exemples

• Pour l'espace euclidien, la courbure scalaire est nulle.

• Pour la sphère de dimension n rayon un, la courbure scalaire vaut n(n − 1).