Réseau de Bravais - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En cristallographie, un réseau de Bravais est une distribution régulière de points – appelés nœuds – dans l’espace qui représente la périodicité de la distribution atomique d’un cristal. Les nœuds peuvent être imaginés comme les sommets des mailles, c'est-à-dire des portions de l'espace dans lesquelles la structure cristalline peut être divisée. La structure est alors reconstruite par simple translation de la maille. La donnée d'un réseau de Bravais n'est pas suffisante pour caractériser un cristal : d'une part le cristal est constitué d'atomes et non de nœuds, et d'autre part la maille peut contenir plusieurs atomes, ce qui fait que certaines symétries du réseau ne sont pas forcement des symétries de la structure cristalline : c'est le cas des cristaux mérièdres. Lorsque que la symétrie complète du réseau de Bravais est réalisée aussi dans la structure cristalline on parle de cristaux holoèdres.
Formellement, un réseau de Bravais en dimension n est défini comme l'ensemble des vecteurs {ma + ma + ... + ma}, où m, ..., m appartiennent à Z et où les vecteurs de base du réseau a, ..., a sont n vecteurs linéairement indépendants. Les paramètres du réseau sont constitués des longueurs a, ..., a et des angles entre les vecteurs de base du réseau.
La périodicité engendre un groupe de symétrie constitué des opérations de translation et de rotation laissant le réseau de Bravais invariant. Si le nombre de réseaux est infini, puisqu'à chaque valeur des paramètres il correspond un réseau différent, le nombre de types de réseaux est fini, le type d'un réseau étant défini par son groupe de symétrie. On dénombre ainsi 5 types de réseau de Bravais dans l'espace bidimensionnel et 14 types dans l'espace tridimensionnel.
Lorsqu'il existe dans un cristal une invariance par rotation, on dit qu'il existe un axe de symétrie d'ordre 2, 3, 4 ou 6, selon que la rotation en question corresponde respectivement à un angle de ± 180°, ± 120°, ± 90° ou ± 60°. L'étude des réseaux de Bravais à l'aide de la théorie des groupes a montré que dans les espaces bidimensionnel et tridimensionnel il n'existe pas de cristal ayant un axe de symétrie d'ordre 5. Ceci n'est plus vrai si la périodicité de la distribution atomique n'est pas parfaite, comme c'est le cas dans un quasi-cristal.
Un réseau étant infini, il est décrit par une maille, qui représente l’unité par répétition infinie de laquelle le réseau est obtenu. Le choix de la maille n’est pas unique, chaque réseau pouvant en principe être décrit par une infinité de mailles différentes ; toutefois, deux types de mailles sont utilisés le plus souvent : la maille primitive (ou élémentaire) et la maille conventionnelle. Les cristaux dont les mailles conventionnelles sont transformées l'une en l'autre en ajoutant ou supprimant des nœuds soit au centre des faces, soit à l'intérieur du volume de la maille, appartiennent à la même famille cristalline.
Mathématiques
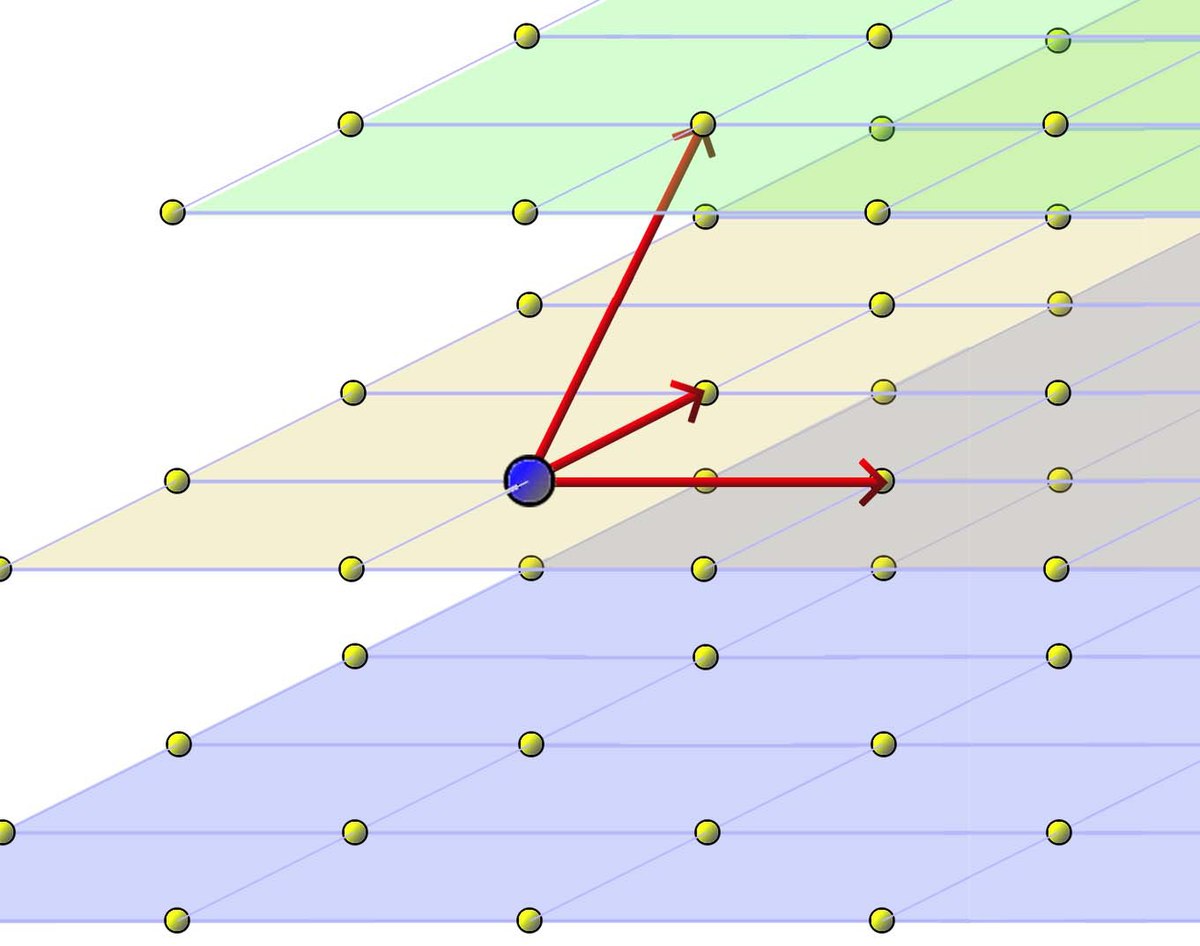
Un réseau de Bravais correspond à une question d'ordre mathématique. Il est associé à l'étude d'un quasi espace vectoriel, la différence entre un espace vectoriel et un réseau étant que dans ce dernier les scalaires sont des entiers et non plus des nombres inversibles (à l'exception de 0) comme les réels ou les complexes. Pour bénéficier d'une géométrie aisément préhensible, le réseau est plongé dans un espace vectoriel euclidien de dimension minimale. Cet espace est, par définition d'un réseau, de dimension finie. Enfin, le réseau peut également être vu comme un espace affine.
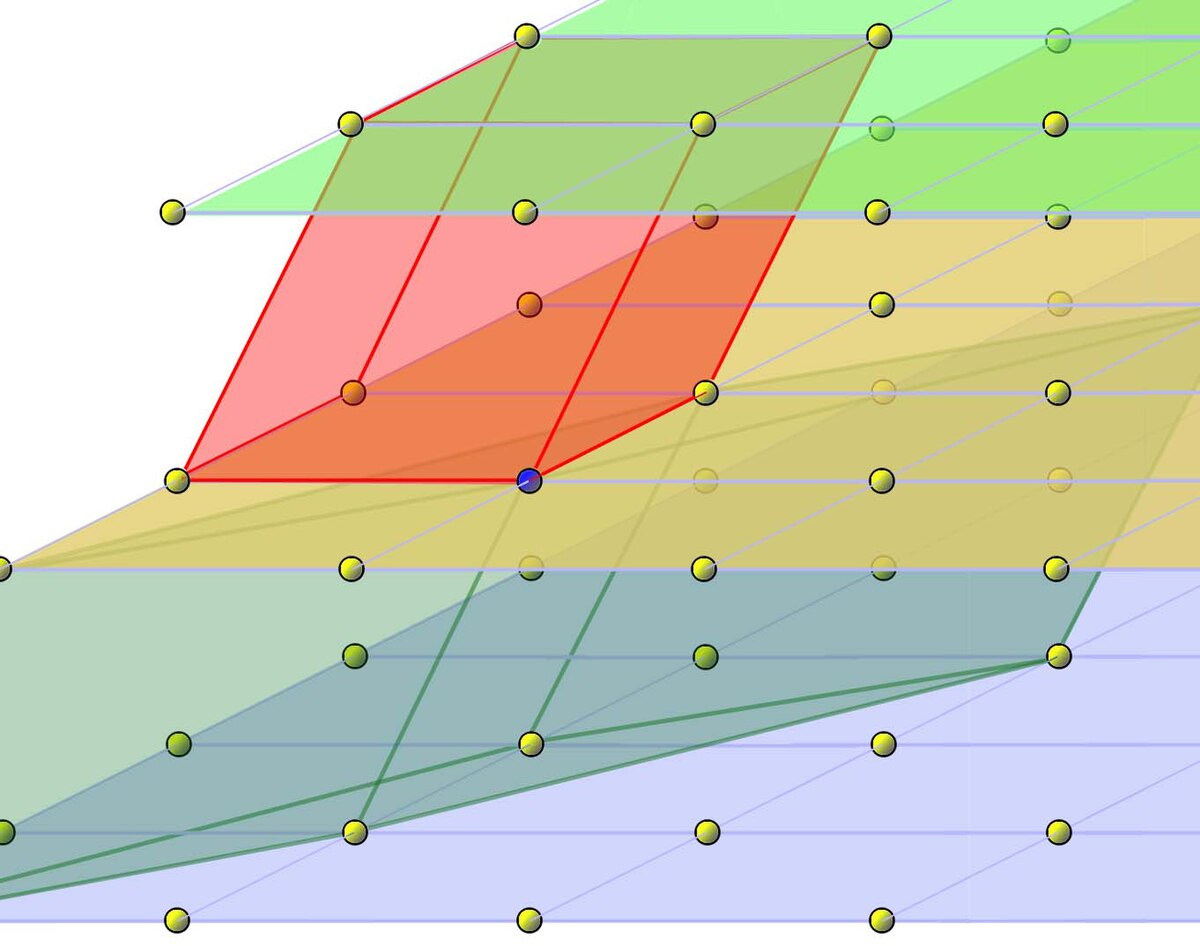
Une des premières propriétés est le fait que, à l'image de la structure d'espace vectoriel, il existe une base et, si une telle base n'est pas unique, son volume l'est. Le domaine fondamental d'une base est formé par l'ensemble des vecteurs dont les coordonnées dans la base sont dans l'intervalle [0,1[, ce que le cristallographe appelle la maille primitive. La figure de droite illustre deux domaines fondamentaux, en vert et en rouge, nécessairement de même volume.
Plusieurs groupes apparaissent naturellement dans l'étude des réseaux de Bravais. Tout d'abord, comme dans un espace vectoriel, le réseau forme un groupe pour l'addition des vecteurs. Ce groupe est isomorphe au groupe des translations laissant le réseau invariant. Ensuite, une question importante est celle du groupe orthogonal, appelé parfois groupe ponctuel de symétrie. Il est composé des applications linéaires qui conservent les distances et les angles, à l'image d'une rotation ou d'une réflexion dans un miroir. Ces transformations forment les isométries vectorielles du réseau. Dans un réseau, le groupe orthogonal est toujours fini et dispose d'une structure de groupe. C'est-à-dire qu'il existe un élément neutre, celui qui ne bouge aucun point du réseau, que l'application réciproque d'une isométrie est encore une isométrie et que la loi de composition des applications linéaires est associative. Enfin, en combinant les deux groupes précédents, on peut former un autre groupe : le groupe d'espace du réseau.
Contrairement au cas des espaces vectoriels, les groupes orthogonaux de deux réseaux de même dimension ne sont pas forcément isomorphes. Élucider la structure du groupe orthogonal d'un réseau de dimension 2 est relativement aisé. Il n'existe que 4 groupes finis possibles et ils sont tous de petits cardinaux : 2, 4, 8 ou 12. Aucun outil sophistiqué n'est nécessaire, il suffit d'utiliser quelques matrices 2x2 pour arriver à ses fins. En dimension 3, la question se corse un petit peu. Le groupe le plus vaste contient 48 éléments. Pour expliciter la structure d'un groupe, il est plus simple de faire appel à la théorie des représentations d'un groupe fini. Un outil un peu abstrait, le caractère permet de résoudre rapidement des questions, d'apparence délicate.
L'article détaillé Réseau (géométrie) fait usage de l'algèbre linéaire pour construire les groupes orthogonaux des réseaux de dimension 2 et de la représentation d'un groupe pour la dimension 3.