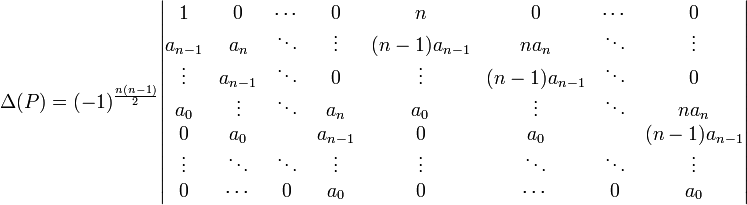Discriminant - Définition
La liste des auteurs de cet article est disponible ici.
Discriminant d'un anneau d'entiers algébrique
La théorie algébrique des nombres utilise la notion de discriminant à partir d'une définition qui semble bien différente. Elle correspond à un déterminant d'une forme quadratique et s'applique à un anneau A. Les deux définitions sont néanmoins intimement corrélées. S'il existe un entier algébrique a tel que l'anneau A est égal à Z[a], ici Z désigne les entiers relatifs, alors le polynôme minimal de a possède ses coefficients dans Z. Son discriminant au sens des polynômes est égal au discriminant de l'anneau au sens de la théorie algébrique des nombres.
Polynôme de degré quelconque
L'extraction de racine d'un polynôme à l'aide du discriminant ne se généralise pas aux degrés supérieurs à deux. Le discriminant d'un polynôme garde néanmoins une utilité.
Dans le cas des équations de degré deux, le discriminant est nul si et seulement si le polynôme possède une racine multiple. L'existence de racine multiple peut avoir d'importantes conséquences. En algèbre linéaire, la présence de racine multiple dans le polynôme minimal d'un endomorphisme modifie sa nature. Cette présence interdit la diagonalisation. Sur les extensions des nombres rationnels, les polynômes irréductibles, c'est-à-dire qui ne sont pas factorisables, n'ont jamais de racine multiple (cf l'article Extension séparable), cette situation n'est pas vraie pour tous les corps. Dans le cadre de la théorie de Galois, cette distinction est importante, les résultats sont différents selon la configuration.
Définition et propriétés
La généralisation du discriminant d'un polynôme de degré quelconque offre un outil permettant de déterminer si ses racines sont simples ou multiples. Dans ce paragraphe A désigne un anneau commutatif, unitaire et intègre et P[X] un polynôme de degré n dont les coefficients sont notés de la manière suivante :
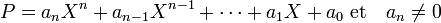
La dérivée formelle de P est notée P' , elle existe même si A est différent du corps des nombres réels ou complexes. Enfin R désigne le résultant, c'est-à-dire une application qui à deux polynômes associe un élément de A.
-
- Le discriminant de P, en général noté Δ(P), est la valeur définie par la formule suivante lorsque deg(P') = n − 1 (avec n = deg(P)) :
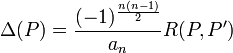
Le coefficient de normalisation possède son importance, un discriminant peut aussi être interprété comme un volume orienté. L'usage d'une telle approche devient évidente lors de l'analyse du discriminant d'une forme quadratique ou d'un anneau de Dedekind dans le cadre de la théorie algébrique des nombres.
Certains résultats de la théorie de Galois s'appliquent au discriminant, il faut alors étendre l'anneau A des coefficients. Comme A est commutatif unitaire intègre, il possède un corps des fractions F commutatif et P peut être considéré comme un polynôme à coefficients dans F. Ici K désigne le corps de décomposition de P, c'est-à-dire le plus petit corps contenant F et toutes les racines de P, à un isomorphisme près. Le discriminant possède la propriété suivante :
-
- Le discriminant du polynôme P est non nul si et seulement il n'admet aucune racine multiple.
La démonstration est une conséquence générale du résultant démontrée dans l'article détaillé. Si un polynôme n'admet aucune racine multiple, il est qualifié de séparable.
Il existe une formule différente permettant d'exprimer le discriminant, à l'aide des racines du polynôme :
-
- Soit αi pour i variant de 1 à n, les racines du polynôme P, le discriminant vérifie l'égalité suivante :
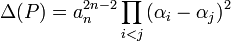
Cette propriété démontre la précédente, elle dérive d'une caractéristique du résultant de deux polynômes. Il est nul si et seulement si les deux polynômes ne sont pas premiers entre eux.
D'après les propriétés du résultant (cf l'article détaillé), le discriminant est égal à :
![R(P,P') = (-1)^{n(n-1)}a_n^{n-1}\prod_{i=1}^n P'[\alpha_i]=a_n^{n-1}\prod_{i=1}^n P'[\alpha_i]](https://static.techno-science.net/illustration/Definitions/autres/c/c0b516bea3ae059fa951df134f763be5_a97b829d331ee99403804dd78cd50091.png)
Le polynôme P vérifie l'égalité suivante, ce qui, par dérivation donne :
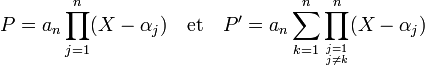
On en déduit l'expression de P' (αj) :
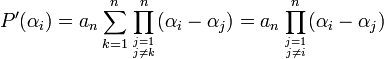
Ce qui fournit l'expression suivante du discriminant :
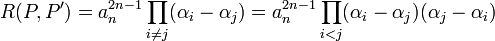
Comme il existe exactement n(n - 1)/2 couples (i, j) tel que i est strictement plus petit que j, on en déduit :
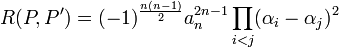
La définition du discriminant permet de conclure.
Exemples
- Pour les polynômes du second degré et avec les notations du premier paragraphe, on obtient :
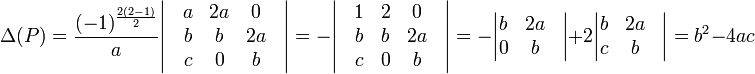
- Pour les polynômes de degré trois on considère généralement le polynôme normalisé, c'est-à-dire celui dont le monôme dominant est égal à 1. et avec les notations suivantes :
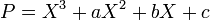
On obtient :
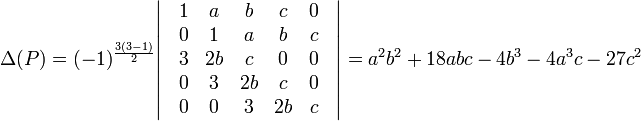
L'expression est un peu complexe, pour cette raison, la tradition est de réaliser des substitutions pour obtenir un polynôme de la forme suivante, le discriminant est alors plus simple :
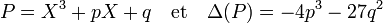
Dans le cas d'une équation polynomiale de degré 3 à coefficients réels, si le discriminant est strictement négatif l'équation admet trois solutions réelles, si le déterminant est nul une racine est multiple et toutes sont réelles, si le déterminant est strictement positif, l'équation n'admet qu'une solution réelle, les deux autres sont complexes conjugués.
- Les courbes elliptiques sont un cas particulier de polynômes du troisième degré à deux variables. Pour le cas simple d'une courbe elliptique de la forme y2 = x3 + ax + b, où les coefficients a,b sont des nombres réels, le discriminant est défini par Δ = − 16(4a3 + 27b2).
Expression générale
L'expression générale du discriminant du polynôme P défini par :
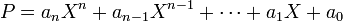
est la suivante :