Énigme des trois maisons - Définition

Solutions avec d'autres géométries

Ruban de Möbius

Sur un ruban de Möbius, une solution existe.

L'impossibilité de résoudre l'énigme est une conséquence du théorème de Jordan. Une géométrie pour laquelle une solution existe doit donc admettre des courbes de Jordan qui ne divisent pas l'espace en deux composantes connexes par arcs. Comme le montre le paragraphe intitulé Topologie géométrique, la recherche d'une solution sur une sphère est vaine, une méthode rapide pour s'en convaincre est de remarquer que le théorème de Jordan est valide sur cette géométrie.

En revanche, le théorème ne s'applique pas si l'espace n'est pas orientable. Dans un espace non orientable, le côté droit de certaines courbes finit par devenir le côté gauche. Autrement dit, le concept de droite et de gauche ne fait pas sens sur un tel espace. Tel est le cas sur un ruban de Möbius. La ligne à égale distance des deux bords possède cette propriété. Placer les trois maisons et les trois fournisseurs sur une telle ligne, à l'image de la figure de gauche, est judicieux. Les six premières canalisations n'ont alors pas coupé la géométrie en deux composantes connexes par arcs.

Pour comprendre ce qu'il advient une fois ces six premières canalisations posées, le plus simple est de construire un ruban de Möbius, de dessiner les différents nœuds et de couper effectivement le ruban. On obtient la figure en haut à droite (on n'a pas représenté la double torsion induite par le découpage dans la mesure où celle-ci ne change pas la résolution de l'énigme). Le ruban devient un unique nouveau ruban, deux fois plus long et deux fois moins large. Une des frontières du ruban contient maintenant deux séries des six nœuds à la suite l'une de l'autre.

Pour une raison de simplicité, il est plus simple de déformer le cylindre obtenu. On resserre la frontière ne contenant pas les nœuds jusqu'à ce que cette frontière soit réduite à un point, on ajoute alors ce point (on a vu précédemment que cela ne change rien à la résolution de l'énigme) pour obtenir un cône. Aplatir ce cône, ce qui ne change encore rien à l'existence ou l'absence de solution, donne la figure en bas à droite. Il devient aisé de trouver comment placer les trois dernières canalisations. La solution en bas à droite est celle qui est illustrée à gauche, une fois réalisées les transformations inverses.

Tore

Le tore ne vérifie pas le théorème de Jordan. La courbe de Jordan verte ne divise pas le tore en deux composantes connexes par arcs.

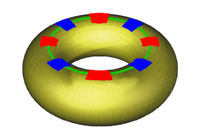
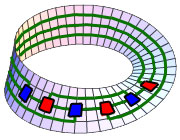
Le ruban de Möbius est un exemple de surface qui ne satisfait pas le théorème de Jordan car il n'est pas orientable. D'autres surfaces sont orientables et ne satisfont néanmoins pas le théorème. C'est le cas du tore. Il existe cette fois, non pas un, mais deux types de courbes de Jordan dont le complémentaire est connexe par arcs. Pour cette raison, il est possible de résoudre l'énigme, même avec quatre maisons et quatre fournisseurs. Le fait de considérer une géométrie contenant un trou, comme le tore autorise la représentation de graphe non planaire. Tout graphe se représente sur une surface ayant un nombre de trous, encore appelé genre de la surface, suffisamment élevé. Sur une telle surface, et à condition de s'y prendre convenablement, il existe deux courbes de Jordan qui ne créent pas de nouvelles faces, l'équation d'Euler s'écrit alors n - a + f = 0. S'il existe quatre maisons et quatre fournisseurs, le graphe est composée de huit nœuds et seize arêtes, ce qui implique l'existence de huit faces. Le nombre moyen d'arêtes par face est le double du nombre d'arêtes, on trouve donc comme valeur moyenne quatre. Comme c'est aussi le nombre minimal d'arêtes pour une face, la solution ne comporte que des faces à quatre arêtes.

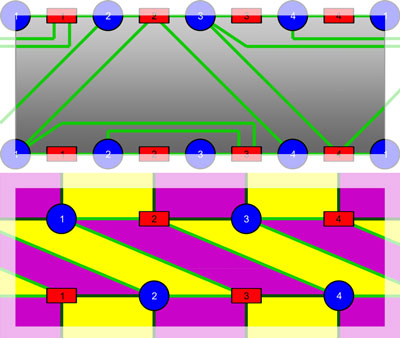
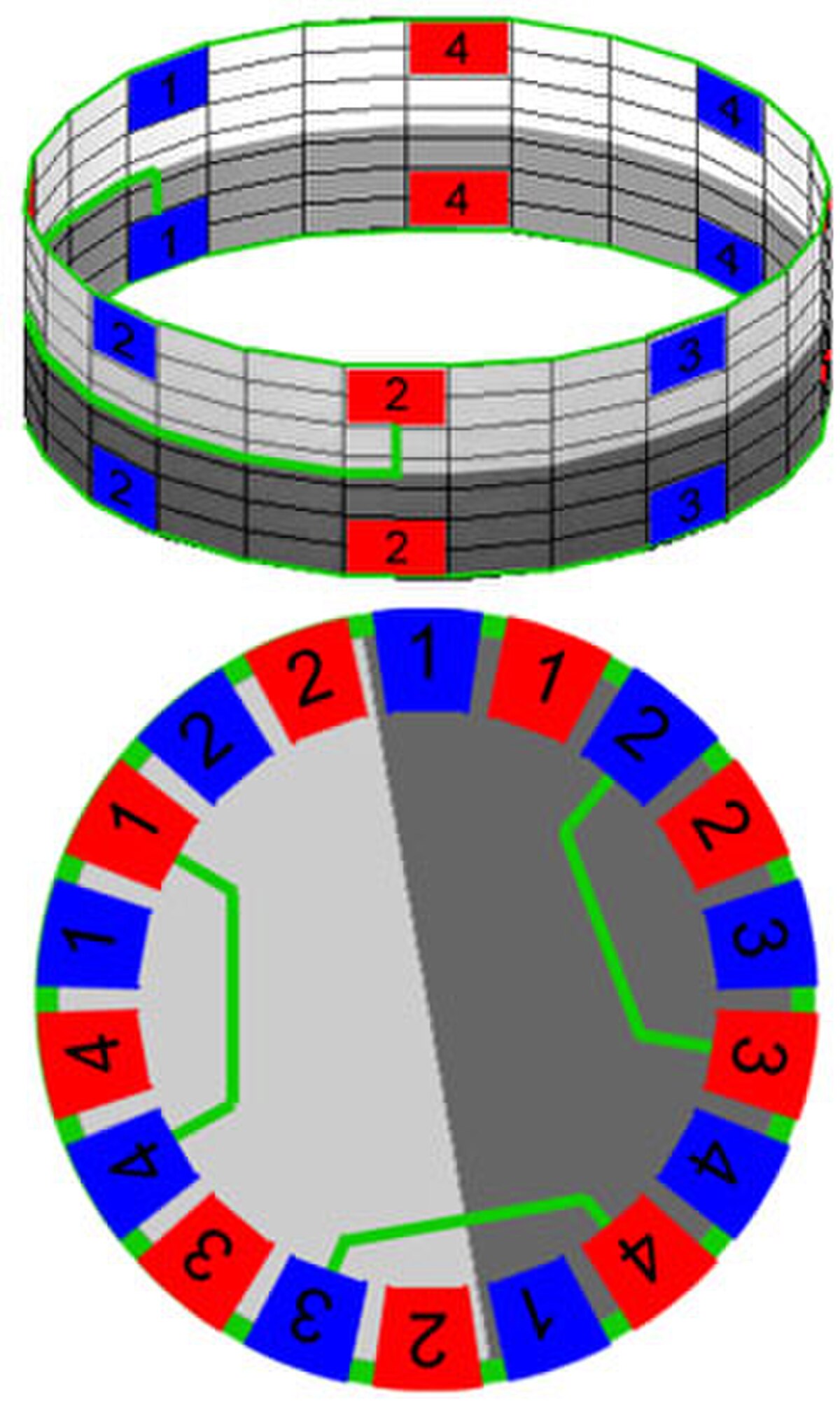
La première courbe de Jordan est illustrée sur la figure en haut à gauche. Comme pour le ruban de Möbius, on obtient un cylindre, illustré à droite. Cette fois-ci, les nœuds ne se trouvent pas tous en haut mais une série est sur la frontière haute et une sur la frontière basse. La technique précédente, pour transformer le cylindre en disque reviendrait à identifier les différents nœuds en un unique point, ce qui n'est pas acceptable. En revanche, il est possible d'établir un lien entre le nœud M₁ situé en bas (avec les notations précédentes M₁ correspond à la première maison. Les maisons sont illustrées en bleu sur les figures) et le nœud F₂ (qui désigne le deuxième fournisseur. Les fournisseurs sont illustrés en rouge sur les figures). Ce lien est illustré en vert sur la figure en haut à droite. On obtient alors une figure comparable à un disque. Ce disque, illustré en bas à droite, comporte dix-huit nœuds. Chaque nœud est représenté deux fois, à l'exception des nœuds M₁ et F₁ qui le sont trois fois. La zone supérieure est représentée en gris clair et celle inférieure en gris foncé. Sous cette forme de disque, trouver la bonne configuration est aisée.

On peut se demander si une solution existe pour cinq fournisseurs et cinq maisons. Le même calcul montre que le nombre moyen d'arêtes par face est égal à dix tiers, soit strictement inférieur à quatre. Or quatre est le minimum d'arêtes pour construire une face pour cette énigme. La recherche d'une solution est donc vaine.

Un raisonnement simple permet de déterminer la bonne configuration et sans tâtonnement. La première courbe de Jordan fournit huit liens. Le neuvième lien transforme la question en un problème plan. Il reste encore sept liens à placer et l'on sait déjà que chaque face (c'est-à-dire chaque composante connexe par arcs du complémentaire) est bordée par exactement quatre liens.

Sous sa forme de disque, on dispose de dix-huit nœuds, qui sont des répétitions des huit nœuds présents sous la forme du tore. Ils sont répétés deux fois, à l'exception des nœuds M₁ et F₂ qui sont répétés trois fois. Sous la forme du disque, l'ajout d'un lien, pour créer des faces contenant quatre liens, se traduit par la pose d'une canalisation qui saute deux nœuds pour se connecter au suivant. Comme, in fine, ce sont les seuls faces qui existent, il est inutile de rechercher d'autres types de pose de canalisation. Placer un lien rend alors inaccessible, sous la forme du disque, les deux nœuds qu'il enserre.

• Liens dix à douze :

Les nœuds M₁ et F₂ disposent de deux spécificités, non seulement ils sont présents trois fois sous la forme de disque, mais, sous la forme torique, ils disposent déjà de trois liens sur quatre. Il est possible, sans dommage, d'enserrer par au moins deux liens ces deux nœuds. Il en restera toujours une instance pour fournir les liens encore manquants. Il existe sur le disque deux séries de nœuds M₁ et F₂ adjacents. Celle du haut sur la figure représentant le disque avec les dix-huit nœuds conduit à la création d'un lien M₂F₁ inutile car déjà existant. Celle du bas permet de créer le lien manquant M₄F₃, c'est celui-ci qu'il faut choisir pour dixième lien.

Les nœuds M₄ et F₃ sont maintenant présents deux fois sur le disque et disposent de trois liens sur quatre dans le tore. On peut donc enserrer une instance de chacun de ces deux nœuds M₄ et F₃ sans dommage. Il est encore possible d'enserrer une instance des nœuds M₁ et F₂ car il reste deux instances disponibles alors qu'un unique lien est manquant pour chacun de ces deux nœuds. On en déduit les deux autres liens, illustrés sur le disque à dix-huit nœuds, en vert. Ce sont les liens onze et douze.

• Quatre derniers liens

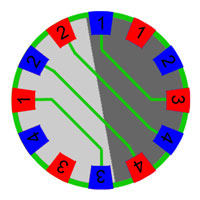
Pour y voir plus clair, le plus simple est de dessiner ce qu'il reste de la plus grande composante connexe par arcs après la pose des douze premières canalisations, illustrée sur la figure de droite. Chaque nœud (vu du point de vue du tore) dispose maintenant de trois liens et il ne manque plus qu'un lien par nœud, or quatre nœuds sont encore représentés deux fois : F₁, M₂, F₃ et M₄. Ce sont donc ces liens qu'il faut enserrer. Il existe deux manières d'enserrer les liens F₁ et M₂. Les deux débouchent chacune sur une solution acceptable. On choisit de poser la canalisation M₁F₃ en haut à droite, qui devient à treizième. Il n'existe alors plus qu'une solution pour enserrer les liens F₃M₄, la quatorzième canalisation relie M₃ à F₁. Les deux dernières sont évidentes et illustrées sur la figure de droite.

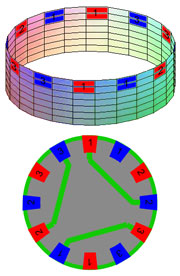
Il reste encore à remonter la solution sur le tore. La convention choisie consiste à représenter un côté de la première courbe de Jordan en gris foncé et l'autre en gris clair. Les canalisations qui restent proches de la première courbe de Jordan restent sur la même couleur, les autres sont celles qui font le tour du tore, à l'image de la neuvième canalisation. On obtient la première figure ci-dessous.

Cette solution n'est encore guère satisfaisante pour comprendre véritablement comment s'organisent les canalisations sur le tore. La représentation géométrique est plus simple en positionnant les nœuds de manière plus géométrique. Posons le tore à plat sur un plan horizontal. Sur le cercle de plus haute altitude, plaçons 4 nœuds sur deux diagonales orthogonales, de manière à ce qu'une diagonale supporte deux maisons et l'autre deux fournisseurs. Le cercle correspond au quatre premières canalisations. Sur le cercle de plus basse altitude, on agit de même, puis on pivote les quatre nouveaux nœuds d'un quart de tour, le cercle de basse altitude correspond à quatre canalisations supplémentaires. En reliant par l'intérieur un nœud au nœud situé exactement au dessous, on obtient encore quatre canalisations. Pour les quatre dernières, imaginons que les canalisations soient élastiques, on relie, à l'aide de quatre canalisations les quatre nœuds supérieurs au quatre nœuds inférieurs en passant par l'extérieur, puis une rotation d'un demi-tour est appliquée aux extrémités inférieures des quatre derniers nœuds. Cette configuration est représentée sur la figure la plus basse. Les huit faces, seize arêtes et huit nœuds sont plus aisément visibles. Les huit liens sombres correspondent à la première courbe de Jordan.

Pour obtenir le tore à partir des figures, il suffit de coller l'arête inférieure du rectangle sur son arête supérieure, puis de coller l'arête de droite, qui est devenue un cercle sur celle de gauche. Les côtés supérieurs et inférieurs du deuxième tore correspondent au cercle de plus petit diamètre du tore.