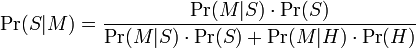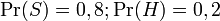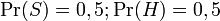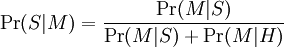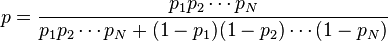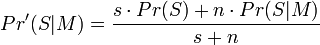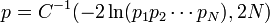Filtrage bayésien du spam - Définition

Discussion

Avantages

L'avantage du filtre bayésien est qu'il s'adapte à son utilisateur.

Le spam qu'un utilisateur reçoit est souvent lié à son activité sur Internet. Par exemple, alors qu'il surfait sur le web, il peut avoir été inscrit à son insu sur une liste de diffusion (présentée comme une « lettre commerciale ») qu'il considérera comme du pourriel. La plupart du temps, l'ensemble des messages envoyés sur cette liste contiennent des mots communs, comme le nom de la liste et l'adresse de courrier électronique de son émetteur. Le filtre bayésien détectera ces points communs et leur attribuera une probabilité élevée.

De la même façon, les courriers légitimes reçus par plusieurs utilisateurs tendent à être différents. Par exemple, en milieu professionnel, le nom de la société où l'on travaille ainsi que les noms des clients et fournisseurs seront mentionnés souvent. Le filtre attribuera une probabilité basse aux courriers contenant ces noms.

Les probabilités peuvent évoluer au fil du temps, au moyen de l'apprentissage continu, à chaque fois que le filtre classe mal un message. Il en résulte qu'un filtre bayésien est souvent plus précis que des règles prédéfinies.

Les filtres bayésiens évitent particulièrement bien les faux positifs, c'est-à-dire de classer les messages légitimes comme des pourriels. Par exemple, si le courriel contient le mot « Nigeria », qui apparaît souvent dans les pourriels de type arnaque nigériane, un jeu de règles prédéfinies le rejettera d'office. Un filtre bayésien marquerait le mot « Nigeria » comme caractéristique de spam, mais prendrait aussi en compte d'autres mots importants, comme par exemple le nom du conjoint ou les noms d'amis, qui sont habituellement des signes de courriers légitimes et prendront le pas sur la présence du mot « Nigeria ».

Inconvénients

L'empoisonnement bayésien (bayesian poisoning) est une technique utilisée par les polluposteurs pour tenter de dégrader l'efficacité des filtres antipourriels bayésiens. Elle consiste à placer dans le courrier une grande quantité de texte anodin (provenant de site d'actualités ou de la littérature par exemple), pour noyer le texte indésirable et tromper le filtre. Ils combattent le filtrage statistique en insérant de grandes quantité de texte anodin ou de salade textuelle, c'est-à-dire des séquences aléatoires de mots qui semblent cohérentes mais qui ne veulent rien dire.

Une autre technique pour essayer de tromper le filtre bayésien est de remplacer le texte par des images. L'ensemble du texte, ou une partie de celui-ci, est remplacé par une image où ce même texte est « dessiné ». Le filtre de pourriel est d'ordinaire incapable d'analyser cette image qui contient les mots sensibles comme « Viagra ». Néanmoins, bon nombre d'utilisateurs désactivent l'affichage des images pour des raisons de sécurité, ce qui fait que les polluposteurs atteignent moins leurs cibles. De plus, la taille d'une image est supérieure à celle du texte équivalent, et les polluposteurs ont besoin de plus de bande passante pour envoyer des messages contenant des images. Enfin, certains filtres tendent à décider qu'un message est du pourriel quand il a trop de contenu graphique.

Fondements mathématiques

Les filtres antipourriels bayésiens reposent sur le théorème de Bayes. Le théorème de Bayes est utilisé à plusieurs reprises dans le contexte du pourriel :

• une première fois, pour calculer la probabilité que le message soit un pourriel, sachant qu'un mot donné apparaît dans ce message ;
• une deuxième fois, pour calculer la probabilité que le message soit un pourriel, en considérant tous ses mots, ou un sous-ensemble significatif de ses mots ;
• parfois une troisième fois, pour traiter les mots rares.

Calculer la probabilité qu'un message contenant un mot donné soit un pourriel

Supposons que le message suspect contienne le mot « Replica ». En 2009, la plupart des gens habitués à recevoir du courrier électronique savent qu'il est probable que ce message soit un pourriel, plus précisément une tentative de vendre des contrefaçons de marques de montres célèbres. Le logiciel de détection de pourriel ignore néanmoins de tels faits, tout ce qu'il sait faire est calculer des probabilités.

La formule que le logiciel utilise pour déterminer cette probabilité est dérivée du théorème de Bayes. Il s'agit, dans sa forme la plus générale, de :

où :

• Pr(S | M) est la probabilité que le message soit un spam, sachant que le mot « Replica » y figure ;
• Pr(S) est la probabilité dans l'absolu qu'un message quelconque soit un spam ;
• Pr(M | S) est la probabilité que « Replica » apparaisse dans des messages de spam;
• Pr(H) est la probabilité dans l'absolu qu'un message quelconque ne soit pas un spam (c'est-à-dire du « ham ») ;
• Pr(M | H) est la probabilité que « Replica » apparaisse dans des messages de ham.

(Démonstration : Théorème de Bayes#Autres écritures du théorème de Bayes)

La pourrielleté

Les statistiques récentes montrent que la probabilité actuelle qu'un message quelconque soit un pourriel sont au moins de 80% :

La plupart des logiciels bayésiens de détection du pourriel considèrent qu'il n'y a pas de raison a priori qu'un message reçu soit du spam plutôt que du ham, et considèrent les deux cas comme ayant des probabilités identiques de 50% :

Les filtres qui font cette hypothèse sont dits « non biaisés », ce qui signifie qu'ils n'ont pas de préjugés sur le courrier reçu. Cette hypothèse permet de simplifier la formule générale en :

Cette quantité est appelée pourielleté ou spamicité du mot « Replica » et peut être calculée. Le nombre Pr(M | S) qui apparaît dans cette formule est approché par la fréquence des messages contenant « Replica » parmi les messages identifiés comme du spam pendant la phase d'apprentissage. De manière semblable, Pr(M | H) est approché par la fréquence des messages contenant « Replica » parmi les messages identifiés comme du ham durant la phase d'apprentissage. Pour que ces approximations soient réalistes, l'ensemble de messages « appris » doit être suffisamment grand et représentatif. De plus, il est recommandé que cet ensemble se conforme à l'hypothèse de répartition à 50% entre spam et ham, c'est-à-dire que les corpus de spam et de ham aient la même taille.

Bien entendu, déterminer si un message est un pourriel ou non en se basant uniquement sur la présence du mot « Replica » peut conduire à l'erreur, c'est pourquoi le logiciel antipourriel essaye de considérer plusieurs mots et de combiner leurs pourrieletés pour déterminer la probabilité d'ensemble d'être un pourriel.

Combiner les probabilités individuelles

Le logiciel de filtrage bayésien du spam fait l'hypothèse naïve que les mots présents dans le message sont des évènements indépendants. Cela est faux dans les langages naturels comme le français, où la probabilité de trouver un adjectif, par exemple, est influencée par la probabilité d'avoir un nom. Quoi qu'il en soit, avec cette hypothèse, on peut déduire une autre formule du théorème de Bayes :

où :

• p est la probabilité que le message suspect soit du spam ;
• p₁ est la probabilité p(S | M₁) que ce soit du spam, sachant qu'il contient un premier mot (par exemple « Replica ») ;
• p₂ est la probabilité p(S | M₂) que ce soit du spam, sachant qu'il contient un deuxième mot (par exemple « watches ») ;
• etc...
• p_N est la probabilité p(S | M_N) que ce soit du spam, sachant qu'il contient un Nième mot (par exemple « home »).

(Démonstration:)

De telles hypothèses font du logiciel de filtrage bayésien un processus de classification naïve bayésienne.

Le résultat p est habituellement comparé à un seuil donné pour décider si le message est un pourriel ou non. Si p est en-dessous de ce seuil, le message est considéré comme un probablement légitime. Sinon, il est considéré comme probablement illégitime.

Traiter les mots rares

Dans le cas où le mot « Replica » n'a jamais été rencontré durant la phase d'apprentissage, le numérateur et le dénominateur sont tous les deux nuls. Le logiciel de filtrage du courrier peut décider de rejeter de tels mots pour lesquels on ne dispose pas d'informations.

De façon plus générale, les mots qui n'ont été rencontrés qu'un petit nombre de fois pendant la phase d'apprentissage posent problème, car ce serait une erreur de faire confiance aveuglément à l'information qu'ils nous apportent. Une solution simple est de mettre ces mots aussi de côté.

En appliquant à nouveau le théorème de Bayes, et en supposant que le classement entre pourriels et courrier légitime est une variable aléatoire obéissant à la loi bêta, d'autres logiciels décident d'utiliser une probabilité corrigée :

où :

• Pr'(S | M) est la probabilité corrigée que le message soit du spam, sachant qu'il contient un mot donné ;
• s est la force que nous donnons aux informations sur le spam ambiant ;
• Pr(S) est la probabilité qu'un message entrant soit du spam ;
• n est le nombre d'occurrences de ce mot pendant la phase d'apprentissage ;
• Pr(S | M) est la pourrielleté du mot.

(Démonstration :)

La probabilité corrigée est utilisée à la place de la pourrielleté dans la formule combinant les probabilités de chaque mot.

Pr(S) peut à nouveau être pris égal à 0,5, pour éviter d'obtenir un filtre trop soupçonneux. 3 est une bonne valeur pour s, ce qui veut dire qu'il faut plus de trois messages pour avoir plus confiance dans la valeur de la pourrielleté que dans les informations sur le spam ambiant.

Cette formule peut être étendue au cas où n est nul (et où la pourrielleté n'est pas définie), et donne dans ce cas Pr(S).

Autres heuristiques

Les mots « neutres » comme « le », « la », « un » (en français) ou leurs équivalents dans d'autres langues sont habituellement ignorés.

De façon plus générale, la plupart des logiciels de filtrage bayésiens ignorent purement et simplement tout mot dont la pourrielleté est proche de 0,5, car ils ne contribuent pas à une bonne décision. Les mots pris en considération sont ceux dont la pourrielleté est proche de 0,0 (signes distinctifs de messages légitimes) ou proche de 1,0 (signes distinctifs de messages illégitimes). Une méthode peut consister à ne conserver que les dix mots pour lesquels la valeur absolue | 0,5 − pI | est la plus grande.

Certains logiciels prennent en considération le fait qu'un mot donné apparaît plusieurs fois dans le message examiné, d'autres ne le font pas.

Certains logiciels utilisent des motifs (groupes de mots) au lieu de mots isolés dans la langue naturelle. Par exemple, pour une fenêtre contextuelle de quatre mots, ils calculent la pourrielleté de « Viagra est bon pour », au lieu de calculer les pourrielletés de « Viagra », « est », « bon » et « pour ». Cette méthode donne plus de sensibilité au contexte et élimine mieux le bruit bayésien, mais demande une plus grande base de données.

Méthodes mixtes

Il y a d'autres manières de combiner les probabilités individuelles pour les différents mots que l'approche « naïve ». Ces méthodes divergent de la méthode naïve sur les hypothèses qui sont faites au sujet des données en entrée. Ces hypothèses différentes donnent des formules radicalement différentes pour combiner les probabilités individuelles.

Par exemple, si l'on suppose que les probabilités individuelles suivent une loi du χ² avec degrés de liberté, on peut utiliser la formule :

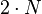
où C ^{− 1} est l'inverse de la fonction χ².

Les probabilités individuelles peuvent être combinées aussi avec les techniques de discrimination markovienne.