Géométrie de contact - Définition
La liste des auteurs de cet article est disponible ici.
Outils de la géométrie de contact
Livre ouvert
La dernière révolution de la topologie de contact en dimension trois est le théorème des livres ouverts de Giroux en 2001. Ce théorème montre que les structures de contact en dimension trois sont des objets purement topologiques et lie les structures de contact en grande dimensions à la géométrie de variétés de Weinstein.
En dimension trois, cette correspondance a permis en particulier la définition de l'invariant d'Ozsváth-Szabó, un nouvel outil particulièrement efficace pour montrer qu'une structure de contact est tendue.
Utilisation des courbes pseudoholomorphes
L'introduction des courbes pseudoholomorphes (ou courbes holomorphes, par abus) par Mikhaïl Gromov en géométrie symplectique a eu de nombreuses applications en géométrie de contact :
- Le théorème d'Eliashberg-Gromov (1990) affirme qu'une structure de contact symplectiquement remplissable est tendue. Plus exactement, le bord convexe d'une variété symplectique compacte est une variété de contact tendue.
- La méthode de Hofer est une approche de la conjecture de Weinstein basée sur les courbes holomorphes.
- La théorie symplectique des champs est une généralisation des invariants de Gromov-Witten dans l'esprit de l'homologie de Floer, elle contient comme cas particulier l'homologie de contact.
Liens avec les feuilletages
Bien qu'une structure de contact semble être l'opposé d'un feuilletage de codimension un, le developpement des deux théories a fait apparaître de nombreux points communs. De plus, la théorie des feuilletacts d'Eliashberg et Thurston est un pont direct entre les deux domaines qui permet notamment de montrer le :
Théorème de perturbation d'Eliashberg-Thurston — Tout feuilletage de codimension un et de régularité au moins C2 sur une variété de dimension trois fermée orientée différente de
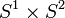
Existence et classification
Modèles locaux
Comme en géométrie symplectique, en dimension 2n + 1, deux variétés de contact sont toutes localement conjuguées. Plus exactement :
Théorème de Darboux — Sur une variété différentielle M de dimension 2n + 1, une structure de contact se définit localement par une forme de contact α ; tout point x de M appartient à un voisinage, domaine d'une carte locale envoyant x sur 0 et α sur la forme de contact canonique de ℝ2n+1 (qui a été donnée dans les exemples ci-dessus).
Les problèmes qui se posent en géométrie de contact sont donc de nature globale. Le premier problème concerne l'existence et/ou l'unicité des structures de contact. Se pose donc le problème de leur classification à contactomorphisme près.
Deux structures de contact sont dites conjuguées (ou isomorphes ou contactomorphes) s'il existe un difféomorphisme qui envoie l'une sur l'autre. Deux structures de contact définies sur la même variété sont dites isotopes s'il existe un tel difféomorphisme qui est de plus isotope à l'identité.
Théorème de Gray — Si ξt,
![t\in[0,1]](https://static.techno-science.net/illustration/Definitions/autres/d/d9a06fde4663cdd5b1ba693e9127232f_ce76be6544934df881b7082a83aabd2d.png)
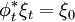
De fait, la classification peut s'effectuer à conjugaison ou à isotopie près.
En dimension 3
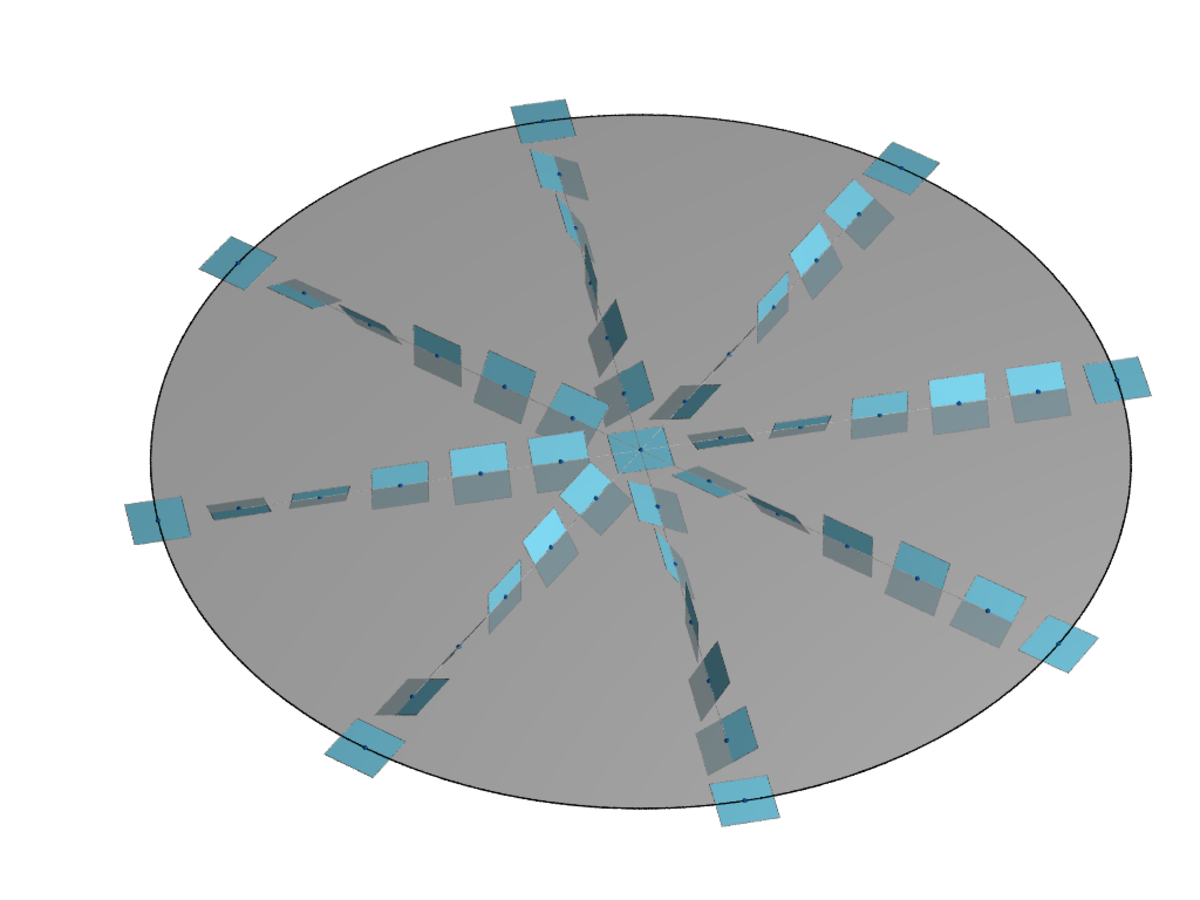
L'existence d'une structure de contact sur une variété différentielle de dimension 3 impose à la variété d'être orientable. En effet, la structure de contact est localement définie comme le noyau de formes de contact αi définies sur des ouverts Ui recouvrant la variété. Pour i et j distincts, on est en mesure d'écrire αi = fijαj où fij est une fonction définie sur l'intersection
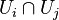
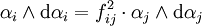
L'orientabilité de la variété est la seule contrainte topologique pour l'existence d'une structure de contact en dimension 3. Non seulement sur une variété orientable de dimension 3 il existe des structures de contact, mais il en existe en nombre suffisant :
Théorème de Lutz et Martinet — Sur toute variété fermée et orientable de dimension 3, tout champ de plans est homotope à une structure de contact. De plus on peut choisir cette structure de contact vrillée (cf. plus bas). En particulier, toute variété fermée orientable de dimension 3 possède une structure de contact.
Structures de contact vrillées
Suivant Eliashberg, on dit qu'une structure de contact en dimension trois est vrillée si elle contient un disque vrillé, c’est-à-dire un disque plongé qui est tangent à la structure de contact le long de son bord (comme le disque gris sur l'illustration). Les structures vrillées sont des objets purement topologiques et flexibles comme le montre le théorème suivant :
Théorème de classification des structures de contact vrillées (Eliashberg 1989) — Sur une variété de dimension 3 compacte sans bord, deux structures de contact vrillées sont isotopes si et seulement si elles sont homotopes parmi les champs de plans.
Structures de contact tendues
Une structure de contact est dite tendue si elle n'est pas vrillée. Vu le théorème de Darboux et le fait que tout compact de ℝ3 peut être envoyé dans une boule arbitrairement petite par une transformation de contact, l'existence de structures tendue nécessite le :
Théorème de Bennequin — La structure de contact canonique sur ℝ3 est tendue.
Cet énoncé est le théorème fondateur de la topologie de contact moderne. Ce théorème possède quatre démonstrations indépendantes. La démonstration initiale de Bennequin repose une étude de théorie des noeuds, elle reste en dimension trois. La preuve d'Eliashberg et Gromov en 1991 utilise le remplissage de la sphère S3 par la boule de dimension quatre et la théorie des courbes pseudoholomorphes, elle est donc de nature analytique. La preuve de Giroux en 2000 utilise les lemmes de bifurcation, elle est purement topologique et reste en dimension trois. Enfin la preuve de Ozvath et Szabo en 2002 utilise l'homologie d'Heegaard-Floer et donc les courbes pseudoholomorphes. Le premier corollaire de ce théorème est l'existence d'une structure de contact exotique sur ℝ3 puisqu'il est facile de définir une structure de contact vrillée sur ℝ3.
L'étude topologique systématique des structures de contact tendues a été rendue possible à partir de 1991 par la théorie des surfaces convexes de Giroux. Cette théorie a ensuite été développée principalement par Giroux et Honda. Elle permet de classifier complètement les structures de contact tendues sur les espaces lenticulaires, les fibrés en tores sur le cercle, le tore plein, le tore épais et certains fibrés de Seifert.
Bien qu'il n'existe pas de classification générale des structures de contact tendues en dimension trois, les résultats suivants donnent un bon panorama :
Théorème de décomposition en somme connexe — L'ensemble des structures de contact tendues sur une somme connexe
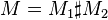
On peut donc restreindre l'étude aux variétés irréductibles. Le premier résultat général dans ce cadre fut
Théorème d'infinitude pour les variétés toroïdales — Toute variété de dimension trois compacte, sans bord, orientable et toroïdale possède une infinité de structures de contact universellement tendues.
La réciproque de ce théorème est contenue dans le théorème suivant :
Théorème de classification grossière — Soit M une variété de dimension trois compacte, sans bord et orientable.
- Le nombre de classes d'homotopies de champs de plans sur M contenant une structure de contact tendu est fini.
- Si M est atoroïdale alors l'ensemble des structures de contact tendues à isotopie près est fini.
En grandes dimensions
La compréhension des structures de contact en grande dimension est encore embryonnaire comparée à ce qui est connu en dimension 3. L'existence n'est plus automatique et le seul résultat complètement général connu est le théorème des livres ouverts (voir ci-dessous). Un de ses corollaires est la preuve par Bourgeois de l'existence de structures de contact sur tous les tores T2n + 1.
Par ailleurs l'homologie de contact (voir ci-dessous) a permis de mettre à jour de nombreuses structures de contact exotiques sur les sphères.