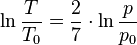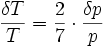Gradient thermique adiabatique - Définition
La liste des auteurs de cet article est disponible ici.
Franchissement d'un obstacle
Supposons un vent sec parallèle au sol qui rencontre un obstacle du relief (colline, montagne). L'air suit le relief et s'élève, il subit donc une détente qui le refroidit. Puis, lorsque l'air redescend sur l'autre versant, il se réchauffe. Si l'opération a été suffisamment rapide, l'air n'a pas échangé de chaleur avec l'obstacle ni avec l'air d'altitude, il se retrouve donc à la même température de l'autre côté.
Maintenant, si l'humidité de l'air est assez importante, l'eau va se condenser en montant. Deux scénarios peuvent se produire :
- S'il ne pleut pas sur le côté face au vent, en redescendant, l'air se réchauffe et donc les gouttelettes d'eau s'évaporent à nouveau. La chaleur libérée par la liquéfaction en montant est réabsorbée par l'évaporation en descendant, l'air a donc également la même température de l'autre côté du versant.
- S'il pleut au sommet de la montagne, cela change les conditions, l'air a perdu une partie de son humidité au sommet de la montagne. Il y a donc moins d'eau qui s'évapore et ainsi moins de chaleur absorbée, l'air de l'autre côté du versant est donc plus chaud à altitude égale à celle de départ.
Bibliographie
- Barry, R.G. et Chorley, R.J. Atmosphere, weather and climate (7ème édition) Routledge 1998 p. 80-81 ISBN 0-415-16020-0
- M K Yau et R R ROGERS, Short Course in Cloud Physics, Third Edition, publié par Butterworth-Heinemann, 1er janvier, 1989, 304 pages. EAN 9780750632157 ISBN 0-7506-3215-1
Annexe : Calcul simplifié
Tout gaz parfait diatomique en évolution adiabatique et quasi-statique, obéit à la loi :
où
- T est la température absolue (en kelvin) pour une pression p ;
- T0 est la température au sol, où la pression est p0
donc le gradient de température δT est relié au gradient de pression δp par la relation
Le tableau de variation de pression avec l'altitude permet donc de déterminer ce gradient thermique :
- on prend p = 1 013 hPa et T = 288,15 K (15 °C) ;
- on considère δp la différence de pression entre deux altitudes du tableau, ce qui donne δT/T la différence de température absolue relative entre deux altitudes ;
- T est alors calculé à partir de la température à l'altitude précédente et du gradient relatif.
Le tableau suivant considère une masse d'air partant du sol et s'élevant.
| altitude (km) | pression (hPa) | température (K) | δp (hPa) | δp/p (sans unité) | δT/T (sans unité) | δT (K) |
|---|---|---|---|---|---|---|
| 0 | 1013 | 288,15 | ||||
| 0,5 | 955 | 283,44 | −58 | −0,057 | −0,016 | −4,71 |
| 1 | 900 | 278,77 | −55 | −0,058 | −0,016 | −4,66 |
| 1,5 | 845 | 273,90 | −55 | −0,061 | −0,017 | −4,87 |
| 2 | 794 | 269,18 | −51 | −0,060 | −0,017 | −4,72 |
| 2,5 | 746 | 264,53 | −48 | −0,060 | −0,017 | −4,65 |
| 3 | 700 | 259,87 | −46 | −0,062 | −0,018 | −4,66 |
| 3,5 | 658 | 255,42 | −42 | −0,06 | −0,017 | −4,45 |
| 4 | 617 | 250,87 | −41 | −0,062 | −0,018 | −4,55 |
| 5 | 541 | 242,04 | −76 | −0,123 | −0,035 | −8,83 |
| 6 | 471 | 233,09 | −70 | −0,129 | −0,037 | −8,95 |
| 7 | 411 | 224,61 | −60 | −0,127 | −0,036 | −8,48 |
| 8 | 357 | 216,18 | −54 | −0,131 | −0,038 | −8,43 |
| 9 | 331 | 211,68 | −26 | −0,073 | −0,021 | −4,50 |
| 10 | 265 | 199,62 | −66 | −0,199 | −0,057 | −12,06 |
| 11 | 227 | 191,44 | −38 | −0,143 | −0,041 | −8,18 |
| 12 | 194 | 183,49 | −33 | −0,145 | −0,042 | −7,95 |
On remarque immédiatement que la température ainsi calculée est très différente de la température de l'air réelle que l'on s'attend à rencontrer.
Si l'on refait le calcul en considérant que la masse d'air part de l'altitude n (donc à la température T) pour aller à l'altitude n+1, on obtient le tableau suivant.
| altitude (km) | pression (hPa) | température (K) | δp (hPa) | δp/p (sans unité) | δT/T (sans unité) | δT (K) |
|---|---|---|---|---|---|---|
| 0 | 1013 | 288,15 | ||||
| 0,5 | 955 | 282,15 | −58 | −0,057 | −0,016 | −4,71 |
| 1 | 900 | 280,15 | −55 | −0,058 | −0,016 | −4,64 |
| 1,5 | 845 | 278,15 | −55 | −0,061 | −0,017 | −4,89 |
| 2 | 794 | 275,15 | −51 | −0,060 | −0,017 | −4,80 |
| 2,5 | 746 | 272,15 | −48 | −0,060 | −0,017 | −4,75 |
| 3 | 700 | 270,15 | −46 | −0,062 | −0,018 | −4,79 |
| 3,5 | 658 | 267,15 | −42 | −0,06 | −0,017 | −4,63 |
| 4 | 617 | 263,15 | −41 | −0,062 | −0,018 | −4,76 |
| 5 | 541 | 257,15 | −76 | −0,123 | −0,035 | −9,26 |
| 6 | 471 | 250,15 | −70 | −0,129 | −0,037 | −9,51 |
| 7 | 411 | 242,15 | −60 | −0,127 | −0,036 | −9,10 |
| 8 | 357 | 235,15 | −54 | −0,131 | −0,038 | −9,09 |
| 9 | 331 | 232,15 | −26 | −0,073 | −0,021 | −4,89 |
| 10 | 265 | 222,15 | −66 | −0,199 | −0,057 | −13,23 |
| 11 | 227 | 218,15 | −38 | −0,143 | −0,041 | −9,10 |
| 12 | 194 | 217,15 | −33 | −0,145 | −0,041 | −9,06 |
Le gradient thermique est défini comme le rapport entre la variation de température δT divisé par la variation d'altitude δz, exprimé en kelvin par kilomètre (K/km), ou, ce qui est équivalent, en degré Celsius par kilomètre (°C/km). Nous présentons ci-dessous un tableau synthétique du gradient thermique adiabatique pour les deux modèles.
| Altitude (km) | Gradient thermique adiabatique (°C/km) | Gradient thermique du modèle OACI (°C/km) | Température (°C) | ||
|---|---|---|---|---|---|
| modèle 1 | modèle 2 | modèle 1 | modèle 2 | ||
| 0,5 | −9,43 | −9,43 | −6,5 | 10 | 9 |
| 1 | −9,33 | −9,29 | 9 | 7 | |
| 1,5 | −9,73 | −9,78 | 1 | 5 | |
| 2 | −9,45 | −9,59 | −4 | 2 | |
| 2,5 | −9,30 | −9,51 | −9 | −1 | |
| 3 | −9,32 | −9,59 | −13 | −3 | |
| 3,5 | −8,91 | −9,26 | −18 | −6 | |
| 4 | −9,09 | −9,51 | −22 | −10 | |
| 5 | −8,83 | −9,26 | −31 | −16 | |
| 6 | −8,95 | −9,51 | −40 | −23 | |
| 7 | −8,48 | −9,10 | −49 | −31 | |
| 8 | −8,43 | −9,09 | −57 | −38 | |
| 9 | −4,50 | −4,89 | −61 | −41 | |
| 10 | −12,06 | −13,23 | −74 | −51 | |
| 11 | −8,18 | −9,10 | −82 | −55 | |
| 12 | −7,95 | −9,06 | −90 | −56 | |
On constate que le gradient thermique adiabatique calculé par le modèle 1 et par le modèle 2 est assez peu différent, mais que ces valeurs sont très différentes du gradient réel ; le gradient thermique imposé par les températures du sol et de l'espace est donc très différent du gradient thermique adiabatique.
On remarque également que dans le modèle OACI, si une masse d'air s'élève du sol (modèle 1), elle se refroidit plus vite que l'air ambiant (modèle 2, OACI) ; cette masse d'air ascendante va donc échanger de la chaleur avec l'air ambiant et se refroidir, et donc redescendre. Le modèle OACI est donc un modèle d'atmosphère stable.