Kig - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| kde interactive geometry | |
|
| |
| Exemple de construction d'un cercle avec Kig | |
| Développeurs | Devriese, Paolini, Toscano, Pasquarelli, Gatti, Gajdos |
|---|---|
| Dernière version | 1.0 (31 12 2005) [+/−] |
| Environnement | KDE |
| Type | Géométrie dynamique |
| Licence | GNU GPL |
| Site Web | http://edu.kde.org/kig/ |
| modifier | |
Kig (pour KDE interactive geometry) est un logiciel de géométrie dynamique tournant sous environnement KDE. Spécialisé dans la géométrie supérieure, il possède un langage de script, Python, qui lui permet de construire des figures d'une complexité remarquable.
Plateforme
Kig fait intégralement partie du projet Kde-Edu, un paquet de logiciels consacrés à l'éducation qui tourne sous KDE. Seule la plateforme Linux permet donc d'utiliser Kig, à moins d'utiliser Kde for Windows, un logiciel qui émule KDE sous Windows.
Objets
Pour construire trois points par exemple, on doit sélectionner trois fois de suite l'outil point, Kig ne gardant pas en mémoire l'outil sélectionné.
Une fois construits, les objets sont déplaçables avec la souris, et on peut modifier leur couleur et leur taille après leur construction.
Parmi les objets qu'on peut construire avec Kig, il y a
- Le centre de courbure et cercle osculateurs
- Les similitude, affinité, inversion et application projective, l'homologie harmonique
- L'hyperbole de foyers donnés
- L'ellipse de foyers donnés
- L'hyperbole d'asymptotes données, passant par un point donné
- La courbe de Bézier de degré 2 et 3
- La polaire d'un point et le pôle d'une droite par rapport à une conique
- La directrice et les axes radicaux d'une conique, les asymptotes d'une hyperbole, l'hyperbole d'asymptotes données.
- La courbe cubique par 9 points
- La cubique nodale par 6 points
- La cubique cuspidale par 4 points
Formats de fichiers
Outre son propre format de fichier (extension "kig") qui est une description de la figure au format xml, Kig est capable d'exporter en svg ou en LaTeX, et d'importer en partie les figures aux formats DrGeo et Cabri Géomètre.
Scripts Python
Dans la figure
Pour ajouter à la palette d'outils de Kig, un script en Python (langage), il est nécesaire de le convertir en macro.
Par exemple, si on souhaite créer une fonction carré, on incorpore à la figure un objet de type nombre (par exemple 3) et on clique sur ce nombre lorsqu'on crée un objet de type script Python. Le script a alors une donnée d'entrée nommée arg1 et le script peut être le suivant:
def square( arg1 ): return DoubleObject( arg1.value()**2 )
L'antécédent de la fonction est la valeur de l'argument arg1; on l'élève au carré et on retourne le résultat.
Dans la figure, le nombre 9 apparaît (en effet 32 = 9) et pour avoir un objet utilisable en Kig, il reste à créer une macro en sélectionnant le 3 comme objet initial et le 9 comme objet final. Un nouvel outil apparaît alors dans la palette de Kig. La manipulation est à comparer avec la version DrGeo.
Les objets considérés ne sont pas nécessairement numériques: Si au moment de la création du script, on désigne un point comme argument (en cliquant dessus), arg1 sera un point et plus un nombre. On peut alors lui appliquer le script suivant:
def csquare( arg1 ): x=arg1.coordinate().x y=arg1.coordinate().y z=x*x-y*y y=2*x*y x=z return Point( Coordinate(x,y) )
Ce script crée un point qui est l'image du précédent par la transformation
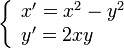
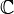
Cette méthode enrichit Kig mais seul un objet peut être retourné. Pour construire une figure complexe en Python, il faut utiliser un programme appelé pykig.py et fourni avec Kig.
Avec pykig
Le script doit être écrit avec un éditeur de texte externe (après avoir quitté Kig) et lancé en ligne de commande avec pykig.py LeScript.kpy (s'il a été enregistré sous le nom LeScript.kpy). S'il n'y a pas d'erreur de syntaxe, l'exécution du script a pour effet de lancer Kig avec la figure telle qu'elle a été construite.
Par exemple, pour construire le triangle de Sierpinski dynamique, le script est le suivant:
from random import * kigdocument.hideobjects() A=Point(0,2) A.show() B=Point(-2,-1) B.show() C=Point(2,-1) C.show() M=Point(.1,.1) for i in range(1,1000): d=randrange(3) if d==0: s=Segment(A,M) M=s.midpoint() if d==1: s=Segment(B,M) M=s.midpoint() if d==2: s=Segment(C,M) M=s.midpoint() M.show()
Cette version est à comparer avec la version CarScript et avec la version (récursive) de DrGeo.
| Géométrie dynamique |
| Logiciels |
|---|
| C.a.R. - Cabri Géomètre - GeoGebra - CaRMetal - DrGeo - Kig - GéoPlan - GéoSpace - GEONExT - TracenPoche |