Logique mathématique - Définition

Système logique

Définition

Un système logique ou système de déduction est constitué de trois composantes. Les deux premières définissent sa syntaxe, la troisième sa sémantique :

• Un ensemble de formules, ou faits ; dans les systèmes de logique classique ou intuitionniste, les formules représentent des énoncés mathématiques exprimés formellement. Les formules sont définies par des moyens combinatoires : suites de symboles, arbres étiquetés, graphes...

• Un ensemble de déductions ; les déductions sont également définies par des moyens combinatoires. Une déduction permet de dériver des formules (les formules prouvables ou théorèmes) à partir de formules de départ (les axiomes) au moyen de règles (les règles d'inférence).

• Une interprétation des formules ; il s'agit d'une fonction associant à toute formule un objet dans une structure abstraite appelée modèle, ce qui permet de définir la validité des formules.

Syntaxe et sémantique

La caractéristique principale des formules et des déductions est qu'il s'agit d'objets finis ; plus encore, chacun des ensembles de formules et de déductions est récursif, c'est-à-dire que l'on dispose d'un algorithme qui détermine si un objet donné est une formule correcte ou une déduction correcte du système.

La sémantique, au contraire, échappe à la combinatoire en faisant appel (en général) à des objets infinis. Elle a d'abord servi à « définir » la vérité. Par exemple, en calcul des propositions, les formules sont interprétées par des éléments d'une algèbre de Boole ; les formules valides sont celles qui sont interprétées par le plus grand élément.

Une mise en garde est de rigueur ici, car Kurt Gödel (suivi par Alfred Tarski) a montré avec son théorème d'incomplétude l'impossibilité de définir mathématiquement la vérité mathématique. C'est pourquoi il est plus approprié de voir la sémantique comme une métaphore : les formules — objets syntaxiques — sont projetées dans un autre monde, plus abstrait, par exemple les algèbres de Boole. Cette technique — plonger les objets dans un monde plus vaste pour mieux raisonner dessus — est couramment utilisée en mathématique et a amplement démontré son efficacité.

Ainsi la sémantique ne sert pas qu'à « définir » la vérité. Par exemple, la sémantique dénotationnelle est une interprétation, non des formules, mais des déductions visant à capturer leur contenu calculatoire.

Systèmes de déduction

En logiques classique et intuitionniste, on distingue deux types d'axiomes : les axiomes logiques qui expriment des propriétés purement logiques comme par exemple (principe du tiers exclu, valide en logique classique mais pas en logique intuitionniste) et les axiomes extra-logiques qui définissent des objets mathématiques, par exemple les axiomes de Peano qui définissent l'arithmétique ou les axiomes de Zermelo-Fraenkel qui définissent la théorie des ensembles. Quand le système possède des axiomes extra-logiques, on parle de théorie axiomatique. L'étude des différents modèles d'une même théorie axiomatique est l'objet de la théorie des modèles.

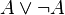
Deux systèmes de déduction peuvent être équivalents au sens où ils ont exactement les mêmes théorèmes. On démontre cette équivalence en fournissant des traductions des déductions de l'un dans les déductions de l'autre. Par exemple, il existe (au moins) trois types de systèmes de déduction équivalents pour le calcul des prédicats : les systèmes à la Hilbert, la déduction naturelle et le calcul des séquents. On y ajoute parfois le style de Fitch qui est une variante de la déduction naturelle dans laquelle les démonstrations sont présentées de façon linéaire.

Alors que la théorie des nombres démontre des propriétés des nombres, on notera la principale caractéristique de la logique en tant que théorie mathématique : elle « démontre » des propriétés de systèmes de déduction dans lesquels les objets sont des « théorèmes ». Il y a donc un double niveau dans lequel il ne faut pas se perdre. Pour clarifier les choses, les « théorèmes » énonçant des propriétés des systèmes de déduction sont parfois appelés des « métathéorèmes ». Le système de déduction que l'on étudie est appelé la « théorie » et le système dans lequel on énonce et démontre les métathéorèmes est appelé la « métathéorie ».

Les propriétés fondamentales des systèmes de déduction sont les suivantes.

• La correction : La correction énonce que les théorèmes sont valides dans tous les modèles. Cela signifie que les règles d'inférence sont bien adaptées à ces modèles, autrement dit que le système de déduction est une manière de bien raisonner dans ces modèles.

• La cohérence : Un système de déduction est cohérent (on dit aussi qu'il est consistant par mimétisme avec l'anglais) s'il admet un modèle non trivial, c'est-à-dire un modèle qui a au moins deux éléments. Cela revient à affirmer que dans ce système de déduction, il existe des propositions qui ne sont pas des théorèmes.

• La complétude : Elle se définit par rapport à une famille de modèles. Un système de déduction est complet par rapport à une famille de modèles, si toute proposition qui est valide dans tous les modèles de la famille est un théorème. En bref, un système est complet si tout ce qui est valide est démontrable.

Une autre propriété des systèmes de déduction apparentée à la complétude est la cohérence maximale. Un système de déduction est maximalement cohérent, si l'ajout d'un nouvel axiome qui n'est pas lui-même un théorème rend le système incohérent.

Affirmer « tel système est complet pour telle famille de modèles » est un exemple typique de métathéorème.

Dans ce cadre, la notion intuitive de vérité donne lieu à deux concepts formels : la validité et la démontrabilité. Les trois propriétés de correction, cohérence et complétude précisent comment ces notions peuvent être reliées, espérant qu'ainsi la vérité, quête du logicien, puisse être cernée.