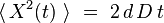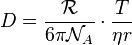Mouvement brownien - Définition
La liste des auteurs de cet article est disponible ici.
Approche mathématique
Notion de processus stochastique
La difficulté de modélisation du mouvement brownien réside dans le fait que ce mouvement est aléatoire et que statistiquement, le déplacement est nul : il n'y a pas de mouvement d'ensemble, contrairement à un vent ou un courant. Plus précisément :
- à un instant donné, la somme vectorielle des vitesses de toutes les particules s'annule (il n'y a pas de mouvement d'ensemble) ;
- si l'on suit une particule donnée au cours du temps, le barycentre de sa trajectoire est son point de départ, elle « virevolte » autour du même point.
Il est difficile dans ces conditions de caractériser le mouvement. La solution fut trouvée par Louis Bachelier, et présentée dans sa thèse soutenue le 29 mars 1900. Il démontra que ce qui caractérise le mouvement, ce n'est pas la moyenne arithmétique des positions <X> mais la moyenne quadratique
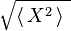
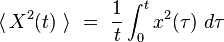
On démontre que le déplacement quadratique moyen est proportionnel au temps :
|
|
où d est la dimension du mouvement (linéaire, plan, spatial), D le coefficient de diffusion, et t le temps écoulé.
Définition mathématique
On peut définir de façon formelle un mouvement brownien: c'est un processus stochastique
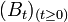
Cette définition permet de démontrer des propriétés du mouvement brownien, comme par exemple sa continuité (presque sure), le fait que presque surement, la trajectoire n'est différentiable nulle part, et de nombreuses autres propriétés.
On pourrait également définir le mouvement brownien par rapport à sa variation quadratique moyenne. Cette définition, classiquement appelée théorème de Levy, donne la caractérisation suivante: un processus stochastique à trajectoires continues dont la variation quadratique est t est un mouvement brownien. Ceci se traduit mathématiquement par le fait que pour une filtration donnée,
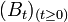
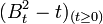
Construction mathématique
En essayant de formaliser le Mouvement Brownien, on peut construire ce dernier suivant deux methodes.
Au moyen du Théorème de Consistance de Kolmogorov :
Soit
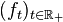
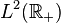
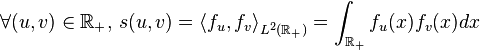
Alors, la fonction satisfait la propriété suivante :
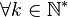
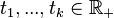
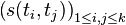
Au moyen du Theoreme de Consistance de Kolmogorov, on peut construire un processus gaussien
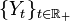
Lorsque
![(f_t)_{t\in{\mathbb{R}}_+}=\left(\sqrt{c}.1\!\!1_{[o,t]} \right)_{t\in\mathbb{R}_+}](https://static.techno-science.net/illustration/Definitions/autres/e/e8e587ee0179f1a5be662d34c4eeaeac_eb04bc22cb4d474e0e1d047138dcd0bb.png)
![1\!\!1_{[o,t]}](https://static.techno-science.net/illustration/Definitions/autres/4/4d26ac9ad1e5001321f8a99179339bdb_31ff3fa4e0c177b57b8067813d170eb2.png)
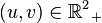
![s(u,v)=c\int\limits_{\mathbb{R}}1\!\!1_{[o,u]}(s)1\!\!1_{[o,v]}(s)ds=\text{c.min}(u,v)](https://static.techno-science.net/illustration/Definitions/autres/8/89a12cfc2dedd4cc202a92c50be42d55_99246d5478b42f8dba1b825845c0860f.png)
Dans ce cas la, la matrice
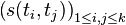
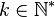
On dit qu'un processus gaussien à valeur réelle indexé par
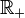
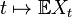
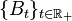
Au moyen d'une serie aléatoire :
Proprietés du Mouvement Brownien
- Le MB part toujours de 0 (ie. on a B0 = 0 p.s.).
- Les accroissements du MB sont indépendants : pour tout
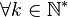
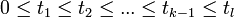
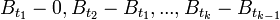
- Pour tous
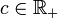
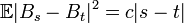
- Le MB est à accroissement stationnaire. Cela signifie que pour tout
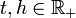
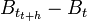
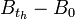
Formule d'Einstein
La formule précédente permet de calculer le coefficient de diffusion d'un couple particule-fluide. En connaissant les caractéristiques de la particule diffusante ou du fluide, on peut en déduire les caractéristiques de l'autre. En connaissant les caractéristiques des deux, on peut évaluer le nombre d'Avogadro à l'aide de la formule d'Einstein (1905) :
où

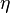

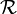
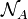
Considérations énergétiques
La quantité d'énergie mise en œuvre par le mouvement brownien est négligeable à l'échelle macroscopique. On ne peut pas en tirer de l'énergie pour réaliser un mouvement perpétuel de seconde espèce, et violer ainsi le deuxième principe de la thermodynamique.
Toutefois, il a été démontré que certains processus biologiques à l'échelle cellulaire peuvent orienter le mouvement brownien afin d'en soutirer de l'énergie.Cette transformation ne contrevient pas au deuxième principe de la thermodynamique tant et aussi longtemps qu'un échange de rayonnement peut maintenir la température du milieu donc la vitesse moyenne des particules. Il faut aussi considérer que la dissipation de ce mouvement brownien sous forme d'énergie utilisable engendre une croissance de l'entropie globale du système (ou de l'univers).