Nombre premier - Définition
La liste des auteurs de cet article est disponible ici.
Des formules sur les nombres premiers
De nombreuses formules ont été cherchées pour générer les nombres premiers. Le plus haut niveau d'exigence serait de trouver une formule qui à un entier n associe le ne nombre premier. De manière un peu plus souple, on peut se contenter d'exiger une fonction f qui à tout entier n associe un nombre premier et telle que chaque valeur prise ne le soit qu'une fois.
Enfin, on souhaite que la fonction soit calculable en pratique. Par exemple, le théorème de Wilson assure que p est un nombre premier si et seulement si
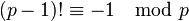
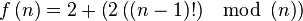
Il est donc tentant de chercher des fonctions polynômes dont les valeurs sont des nombres premiers. Ceci a conduit au résultat (négatif) suivant: un polynôme, à une ou plusieurs variables, dont les valeurs aux entiers naturels sont des nombres premiers, est un polynôme constant.
La recherche de polynômes vérifiant une propriété plus faible s'est développée à partir de la notion d'ensemble diophantien de nombres entiers ; de tels ensembles peuvent être caractérisés comme les ensembles de valeurs strictement positives prises par un polynôme (à plusieurs variables) dont les coefficients et les variables sont des nombres entiers.
Un travail mené dans les années 1960 et 1970, notamment par Putnam, Matijasevic, Davis, Robinson, permet de montrer que l'ensemble des nombres premiers est diophantien, conduisant à l'existence de polynômes à coefficients et variables entières dont toutes les valeurs positives sont les nombres premiers. L'écriture de divers polynômes explicites a ensuite été possible, avec différents nombres de variables, et divers degrés. Notamment, le polynôme suivant, de degré 25 à 26 variables (de a à z), a été déterminé par Jones, Sato, Wada et Wiens en 1976 :
- ( 1
- − [ w.z + h + j − q ]2
- − [ 2.n + p + q + z − e ]2
- − [ a2.y2 − y2 + 1 − x2 ]2
- − [ e3.(e + 2).(a + 1)2 + 1 − o2 ]2
- − [ 16.(k + 1)3.(k + 2).(n + 1)2 + 1 − f2 ]2
- − [ ((a + u2.(u2 − a))2 − 1).(n + 4.d.y)2 + 1 − (x + c.u)2 ]2
- − [ a.i + k + 1 − l − i ]2
- − [ (g.k + 2.g + k + 1).(h + j) + h − z ]2
- − [ 16.r2.y4.(a2 − 1) + 1 − u2 ]2
- − [ p − m + l.(a − n − 1) + b.(2.a.n + 2.a − n2 − 2.n − 2) ]2
- − [ z − p.m + p.l.a − p2l + t.(2.a.p − p2 − 1) ]2
- − [ q − x + y.(a − p − 1) + s.(2.a.p + 2.a − p2 − 2.p − 2) ]2
- − [ a2.l2 − l2 + 1 − m2 ]2
- − [ n + l + v − y ]2
- ) . (k + 2)
De même que pour les formules à factorielles, l'exploitation de ce polynôme ne donne aucun résultat en pratique car il ne donne pratiquement que des valeurs négatives quand on fait varier les variables a à z de 0 à l'infini.
La notion d'ensemble diophantien s'est plus généralement développée à partir des problèmes posés par le dixième problème de Hilbert sur les équations diophantiennes.
Algorithmique : calcul des nombres premiers et tests de primalité
Crible d'Ératosthène et algorithme par essais de division
Les premiers algorithmes pour décider si un nombre est premier (appelés tests de primalité) consistent à essayer de le diviser par tous les nombres inférieurs à sa racine carrée : s'il est divisible par l'un d'entre eux, il est composé, et sinon, il est premier. Cependant, l'algorithme déduit de cette formulation peut être rendu plus efficace : il suggère beaucoup de divisions inutiles, par exemple, si un nombre n'est pas divisible par 2, il est inutile de tester s'il est divisible par 4. En fait, il suffit de tester sa divisibilité par tous les nombres premiers inférieurs à sa racine carrée.
Le crible d'Ératosthène est une méthode, reposant sur cette idée, qui fournit la liste des nombres premiers inférieurs à une valeur fixée n (n = 120 dans l'animation ci-contre) :
- On forme la liste des entiers de 2 à n ;
- On retient comme « nombre premier » le premier nombre de la liste non encore barré (le premier dans ce cas est 2) ;
- On barre tous les entiers multiples du nombre retenu à l'étape précédente, en commençant par son carré (puisque 2*i, 3*i, ...(i-1)*i ont déjà été barrés en tant que multiples de 2, 3, ...) ;
- On répète les deux dernières opérations (c'est-à-dire : on retient le prochain nombre non barré et on barre ses multiples) ;
- Dès qu'on en est à chercher les multiples des nombres excédant la racine carrée de n, on termine l'algorithme.
Ainsi les nombres premiers inférieurs à n sont les nombres qui restent non barrés à la fin du processus. Cet algorithme est de complexité algorithmique exponentielle.
Le crible d'Ératosthène fournit donc plus d'information que la seule primalité de n. Si seule cette information est souhaitée, une variante parfois plus efficace consiste à ne tester la divisibilité de n que par des petits nombres premiers dans une liste fixée au préalable (par exemple 2, 3 et 5), puis par tous les nombres entiers inférieurs à la racine carrée de n qui ne sont divisibles par aucun des petits nombres premiers choisis ; cela amène à tester la divisibilité par des nombres non premiers (par exemple 49 si les petits premiers sont 2, 3 et 5 et que n excède 2500), mais un choix d'un nombre suffisant de petits nombres premiers doit permettre de contrôler le nombre de tests inutiles effectués.
Autres algorithmes
Une variante du crible d'Ératosthène est le crible de Sundaram qui consiste à former les produits de nombres impairs. Les nombres qui ne sont pas atteints par cette méthode sont les nombres premiers impairs, c'est-à-dire tous les nombres premiers sauf 2. Par ailleurs, à partir du crible d'Ératosthène, la factorisation de l'entier n peut facilement être trouvée. D'autres méthodes plus générales concernant ce problème plus difficile que simplement déterminer la primalité sont aussi appelées méthodes de crible, la plus efficace étant actuellement le crible général des corps de nombres.
Les algorithmes présentés précédemment ont une complexité trop importante pour pouvoir être menés à terme, même avec les ordinateurs les plus puissants, quand n devient grand.
Une autre classe d'algorithme consiste à tester l'entier n pour une famille de propriétés vérifiées par les nombres premiers : si une propriété de cette famille n'est pas vérifiée pour n, alors il est composé ; en revanche, le fait qu'une des propriétés de la famille soit vérifiée pour n ne suffit pas à assurer la primalité. Toutefois, si cette famille est telle qu'un nombre composé ne vérifie pas au moins la moitié des propriétés en jeu, alors l'utilisateur peut estimer qu'un nombre n qui vérifie k propriétés de la famille est premier avec une probabilité supérieure à 1-2-k : il est déclaré probablement premier à partir d'une valeur de k à choisir par l'utilisateur ; un nombre déclaré probablement premier, mais qui n'est pas premier est appelé nombre pseudo-premier. Un test basé sur ce principe est appelé test probabiliste de primalité. De tels tests reposent souvent sur le petit théorème de Fermat, amenant au test de primalité de Fermat, et à ses raffinements : le test de primalité de Solovay-Strassen et celui de Miller-Rabin, qui sont des améliorations, car ils admettent moins de nombres pseudo-premiers.
L'algorithme AKS mis au point en 2002 permet de déterminer si un nombre donné N est premier en utilisant un temps de calcul polynomial.

















































