Optique non-linéaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Lorsqu'un milieu matériel est mis en présence d'un champ électrique
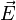
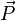
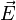
En présence d'une onde électromagnétique du domaine de l'optique (longueur d'onde de l'ordre de 1000 nm), autrement dit, de lumière, beaucoup de matériaux sont transparents, et certains d'entre eux sont non linéaires, c'est pourquoi l'optique non linéaire est possible. Les principales différences avec l'optique linéaire sont les possibilités de modifier la fréquence de l'onde ou de faire interagir entre elles deux ondes par l'intermédiaire du matériau. Ces propriétés étonnantes ne peuvent apparaître qu'avec des ondes lumineuses de forte intensité. C'est pourquoi des expériences d'optique non linéaire n'ont pu être réalisées qu'à partir des années 1960 grâce à l'apparition de la technologie des lasers.
Réponse d'un matériau à l'excitation optique
La polarisation créée par une onde lumineuse traversant un matériau s'écrit sous la forme :
-
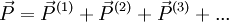
où
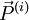
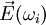
où
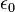
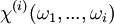
Une interprétation des non-linéarités apparaissant dans la polarisation provient de l'aspect microscopique de la matière. Chaque atome d'un matériau diélectrique est entouré d'un nuage électronique susceptible de se déformer sous l'action de
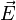
Quelques dispositifs d'optique non linéaire
- Oscillateur paramétrique optique
- Amplificateur paramétrique optique
- Cristal doubleur de fréquence
- Laser accordable
- Fibres à cristaux photoniques
Classification des effets non linéaires
Chaque type de matériau présente des susceptibilités électriques différentes. Ils donnent donc des effets non linéaires de différents ordres. On classe alors ces effets suivant cet ordre.
- Au premier ordre
Seul le premier terme de la polarisation intervient :
-
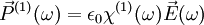
Il s'agit de l'optique linéaire classique où la fréquence de l'onde créée est forcément égale à celle de l'onde initiale. Les effets alors observés sont la réfraction des ondes et la biréfringence.
- Au second ordre
La polarisation s'écrit :
-
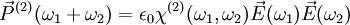
On peut notamment citer les effets suivants :
- la génération de la fréquence somme ω1 + ω2, dont un cas particulier est la génération de seconde harmonique lorsque ω1 = ω2 (lasers doublés en fréquence),
- l'Effet Pockels lorsque ω1 = 0.
- La Rectification Optique est le phénomène réciproque de l'effet Pockels, ou électro-optique. Lorsqu'un cristal non linéaire χ(2) est éclairé par un faisceau lumineux, un champ de polarisation électrique statique est engendré par rectification optique selon le processus :
-
![\vec P^{(2)}(\Omega)=\epsilon_0 \chi^{(2)}\left[\omega +\Omega,-\omega;\Omega\right]\vec E(\omega + \Omega)\vec E^{*}(\omega)](https://static.techno-science.net/illustration/Definitions/autres/b/b31c182539cd6e23d36e52a0733b27ec_200d362ab2f1d1b833a848dec9de52ea.png)
![\vec P^{(2)}(\Omega)=\epsilon_0 \chi^{(2)}\left[\omega +\Omega,-\omega;\Omega\right]\vec E(\omega + \Omega)\vec E^{*}(\omega)](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b31c182539cd6e23d36e52a0733b27ec_200d362ab2f1d1b833a848dec9de52ea.png)
Si des électrodes sont disposées judicieusement sur certaines faces du cristal, une tension électrique apparaît : le signal de rectification optique. Ce dernier est proportionnel à la puissance lumineuse éclairant le cristal, et l'on montre par un traitement quantique que ce dernier constitue un signal de mesure Quantique Non Destructive (QND) du flux lumineux (i.e. flux de photons). De récentes recherches ont été menées dans ce sens au sein du groupe d'Optique Quantique du Laboratoire Kastler Brossel, en collaboration avec une équipe du CEA de Saclay
- Au troisième ordre
La polarisation s'écrit :
-
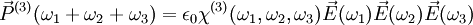
On peut citer les effets suivants :
- le mélange paramétrique à quatre ondes, dont un cas particulier est la génération de troisième harmonique (laser UV),
- les diffusions inélastiques Raman, Brillouin,
- l'effet Kerr,
- la diffusion inélastique Stokes, l'absorption à deux photons et l'émission à deux photons.
