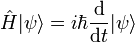Principe de superposition quantique - Définition

Introduction

Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Cette boîte : voir • disc. • mod.

Mesure de la position d'un ensemble de particules étant dans le même état superposé.

En mécanique quantique, le principe de superposition stipule qu'un même état quantique peut possèder plusieurs valeurs pour une certaine quantité observable (spin, position, quantité de mouvement etc.)

Ce principe résulte du fait que l'état - quel qu'il soit - d'un système quantique (une particule, une paire de particules, un atome etc..) est représenté par un vecteur dans un espace vectoriel nommé espace de Hilbert (premier postulat de la mécanique quantique).

Comme tout vecteur de tout espace vectoriel, ce vecteur admet une décomposition en une combinaison linéaire de vecteurs selon une base donnée. Or, il se trouve qu'en mécanique quantique, une observable donnée (comme la position, la quantité de mouvement, le spin etc..) correspond à une base donnée de l'espace de Hilbert.

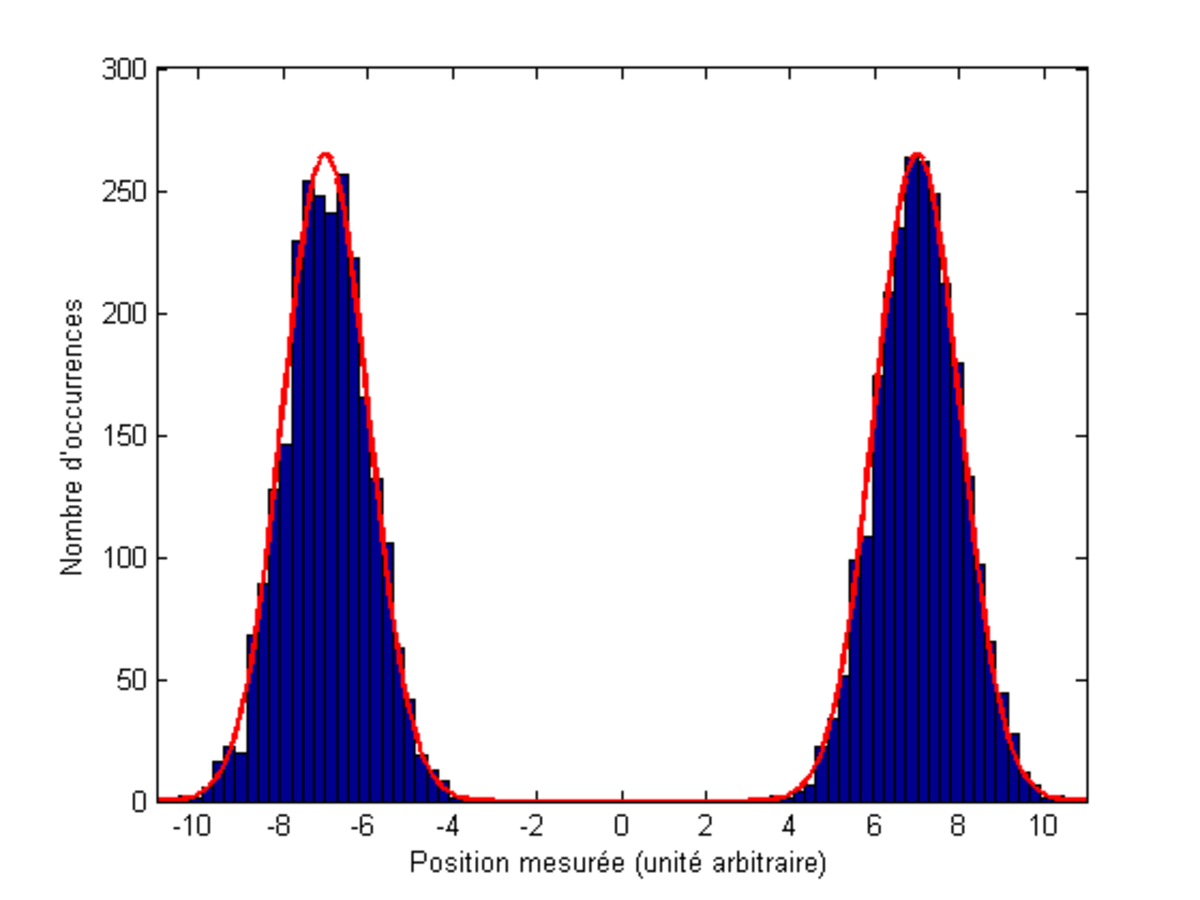
Par conséquent, si l'on s'intéresse à la position (par exemple) d'une particule, l'état de position doit être représenté comme une somme d'un nombre infini de vecteurs, chaque vecteur représentant une position précise dans l'espace. Le carré de la norme de chacun de ces vecteurs représente la probabilité de présence de la particule à une position donnée.

En notation bra-ket la superposition d'un état quantique se note :

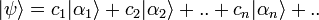
c_i étant le coefficient complexe de la combinaison linéaire, et les vecteurs de la base choisie (qui dépend de l'observable).

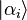
Cette combinaison linéaire est nommé état de superposition, car la particule peut être vue comme étant simultanément, avec des probabilités diverses, en plusieurs endroits. L'état de superposition s'applique de la même façon à toutes les autres observables imaginables : vitesse, spin, ... et même mort/vivant dans le cas du célèbre Chat de Schrödinger.

C'est lors d'une opération de mesure que le vecteur représentant toutes les positions possibles se retrouve projeté sur un des vecteurs de la base, et est donc mesuré à une position (ou toute autre observable) précise (postulat 5 de la mécanique quantique).

Voir aussi