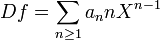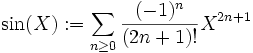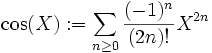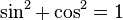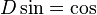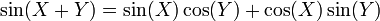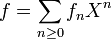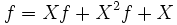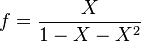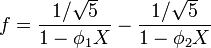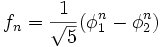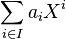Série formelle - Définition

Dérivation de séries formelles

Si f = ∑ a_n X_n est un élément de R[[X]], on définit sa dérivée formelle en utilisant l'opérateur D défini par

Cette opération est R-linéaire :

D(af + bg) = aDf + bDg

pour a, b dans R et f, g dans R[[X]].

Beaucoup de propriétés de la dérivation classique des fonctions sont valables pour la dérivation des séries formelles. Par exemple, la règle de dérivation d'un produit est valable :

D(fg) = f(Dg) + (Df)g

ainsi que la règle de dérivation d'une composée :

D(f(u)) = (Df)(u)Du

Dans un certain sens, toutes les séries formelles sont des séries de Taylor, car si f=∑a_n Xⁿ, en écrivant D_k comme la k^e dérivée formelle, on trouve que

(D_kf)(0) = k!a_k.

On peut également définir la dérivation pour des séries formelles de Laurent d'une façon naturelle, et dans ce cas, la règle du quotient, en plus des règles énumérées ci-dessus, sera également valable.

Propriété universelle

L'anneau des séries formelles R[[X₁, ..., X_r]] possède la propriété suivante :

• Si S est une algèbre commutative et associative sur R
• Si I est un idéal de S tel que S soit complet pour la topologie I-adique
• Si x₁, ..., x_r sont r éléments de I,

Alors, il existe une unique application Φ : R[[X₁, ..., X_r]] -> S vérifiant

• Φ est un homomorphisme d'algèbre
• Φ est continue
• Φ(X_i) = x_i pour tout i = 1, ..., r.

Applications

On peut utiliser des séries formelles pour prouver certaines propriétés en analyse de manière extrêmement simple.

Formules trigonométriques : Considérons les éléments suivants de Q[[X]]:

Alors on peut montrer que

et

aussi bien que

(La dernière expression étant définie sur l'anneau Q[[X,Y]]).

Détermination du terme général d'une suite : Comme exemple de la méthode de la fonction génératrice, considérons le problème consistant à trouver le terme général de la suite de Fibonacci f_n définie par f₀ = 0, f₁ = 1, et f_n = f_n−1 + f_n−2 pour n ≥ 2.

Dans l'anneau R[[X]], on définit la série formelle

f est appelée la fonction génératrice de la suite (f_n). La fonction génératrice de la suite (f_n−1) est Xf et celle de (f_n−2) est X²f. D'après la relation de récurrence sur la suite (f_n), nous pouvons écrire que Xf + X²f est identique à f sauf pour les deux premiers coefficients. On obtient alors la relation

(C'est le point le plus important : une relation de récurrence sur une suite se traduit par une équation sur la fonction génératrice associée). Il suffit alors de résoudre l'équation précédente. On obtient :

Le dénominateur peut se factoriser en utilisant le nombre d'or et son conjugué

et

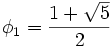
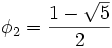
et la décomposition en éléments simples donne

On reconnaît, dans ces deux séries formelles, des séries géométriques. En identifiant leurs coefficients à celui de f, on obtient l'égalité suivante :

Séries formelles généralisées

Soit R un anneau commutatif,

Soit G un groupe commutatif muni d'un ordre total compatible avec l'addition , c’est-à-dire tel que a < b équivaut à a + c < b + c pour tout c de G.

On considère l'ensemble des sous-ensembles I de G bien ordonnés, c'est-à-dire tels que I ne possède pas de chaine infinie décroissante.

On peut alors construire l'ensemble R((G)) des sommes

où a_i sont des éléments de R et où on suppose que, pour chaque ensemble d'indexation I, si tous les a_i sont nul alors la somme est nulle.

Alors R((G)) est l'anneau des séries formelles sur G, car la condition que l'ensemble d'indexation I soit bien ordonné assure que le produit est bien défini. On suppose évidemment que deux éléments qui diffèrent de zéro sont égaux.

Diverses propriétés de R peuvent se transférer à R((G).

Si R est un corps, il en est de même de R((G)).

Si R est un corps ordonné, on peut définir sur R((G)) une relation d'ordre en affectant à chaque série le signe de son coefficient dominant : le coefficient associé au plus petit i tel que a_i soit non nul.

Si G est un groupe divisible et R un corps ordonné tel que R(i) (avec i² = − 1) soit algébriquement clos alors il en est de même de R((G))

Enfin, si G est un groupe divisible et R un corps algébriquement clos alors il en est de même de R((G))

Cette théorie a été développée par le mathématicien autrichien Hans Hahn