Théorème de Jordan - Définition
La liste des auteurs de cet article est disponible ici.
Histoire
Préhistoire

Le théorème de Jordan apparaît tout d'abord dans l'histoire comme une vérité intuitive en deçà des mathématiques. Dessiner une boucle, par exemple rectangulaire, permet de délimiter une zone de l'espace. Cette technique correspond à celle d'un dessinateur de bande dessinée traçant des cadres pour séparer les différentes images narratives. La culture originelle des tchokwés, attestent d'un usage ancien de cette technique graphique pour séparer les membres d'un clan (illustrés à l'intérieur d'une courbe) et les autres (à l'extérieur).
Pour passer d'un pays à un autre, un voyageur traverse nécessairement la frontière. Jusqu'au début du XIXe siècle, ce type de vérité n'a pas à être démontrée. Emmanuel Kant formalise cette vision des choses et estime que les mathématiques sont fondées sur l'évidence intuitive des choses.
Des raisons philosophiques poussent Bernard Bolzano, un mathématicien du début du XIXe siècle, à refuser cette vision. J. Sebestik précise que, pour ce mathématicien : « une démonstration qui fait appel à l'intuition ne fournit que la certitude et ne peut être acceptée que pour des raisons pédagogiques ou heuristiques, seule une démonstration qui fonde une vérité en la rattachant à l'ensemble des vérités d'une science peut être appelé rigoureusement scientifique. ».
Bolzano cherche à démontrer le théorème des valeurs intermédiaires, qui indique en substance que toute personne montant des escaliers pour aller d'un rez de chaussé à un deuxième étage, passe toujours par un premier étage. L'une des difficultés consiste à formuler les bonnes définitions, un résultat atteint en 1814. Bolzano découvre alors des résultats non nécessairement intuitifs : une fonction qui vérifie la propriété de la valeur intermédiaire n'est pas nécessairement continue. Sa définition est toujours d'actualité. Ce mathématicien formalise aussi la notion de connexité. Sa définition correspond à ce que l'on appelle maintenant un connexe par arcs, concept moins général que la définition actuelle, mais plus adaptée aux démonstrations qu'il essaye d'établir.
Ces résultats lui permettent d'exprimer en termes de question mathématique le théorème de l'article, qui quitte le monde des certitudes intuitives pour entrer dans celui des conjectures. Le mathématicien en a conscience et tente des démonstrations. « Comme en témoignent les manuscripts, Bolzano y revient sans cesse. », précise J. Sebestik. Ne disposant pas d'idée originale sur cette question, ses tentatives sont des échecs.
Démonstration de Jordan
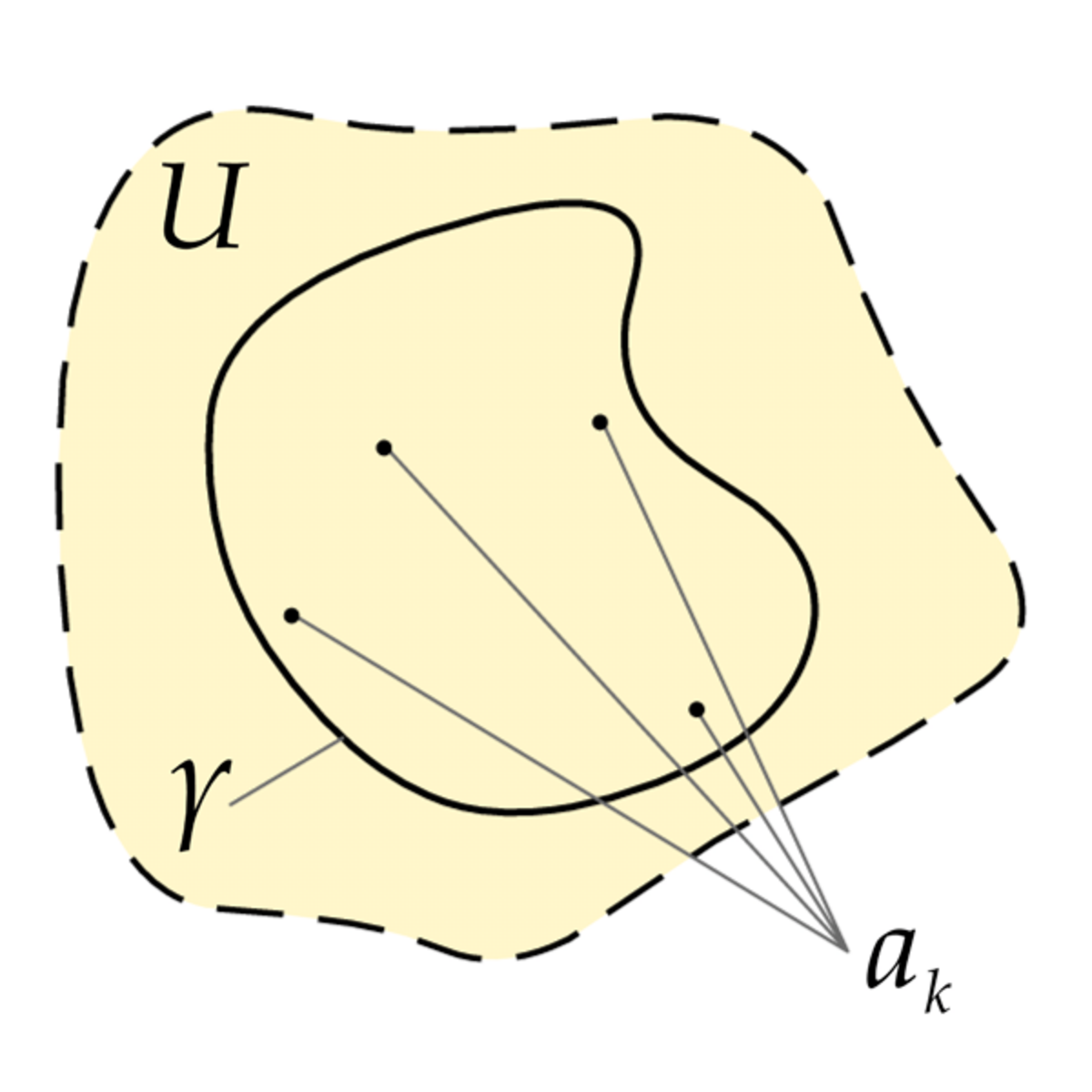
Des décennies sont nécessaires pour que cette conjecture devienne importante et pour que les progrès dans la compréhension de la question permettent enfin une démonstration. Augustin Louis Cauchy développe les prémisses de la théorie des résidus en analyse complexe. L'image d'un lacet simple par une fonction méromorphe f est encore un lacet, les propriétés de ce lacet sont étroitement liées aux singularités de la fonction f situés à l'intérieur du lacet. Montrer que les termes intérieur d'un lacet font sens, est riche de conséquences. L'apparente simplicité d'un lacet simple est petit à petit battue en brèche. Karl Weierstrass prouve en 1872 qu'il existe des courbes partout continues et nulle part dérivables. À la même époque que la démonstration du théorème, Giuseppe Peano montre l'existence de courbes qui remplissent toute une aire plane, un carré en l'occurrence. Ce type de pathologie ne peut arriver dans le contexte de l'article, car si la courbe est un lacet, elle ne peut pas être simple. En revanche, elle met en valeur le rôle non nécessairement intuitif de certaines hypothèses comme l'injectivité du lacet simple.
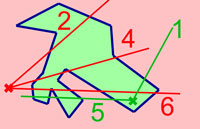
Camille Jordan trouve une idée permettant de conclure. À un point du complémentaire du lacet dans le plan, il associe une demi-droite et compte le nombre de points d'intersection entre cette demi-droite et le lacet. Si ce nombre est fini et à quelques exceptions près, la parité de ce nombre ne dépend pas de la demi-droite choisie. Pour contourner la difficulté représentée par les exceptions, Jordan étudie d'abord le cas des polygones, il ne considère que les demi-droites qui ne passent pas par un sommet, ce qui retire toutes les exceptions. La fonction qui à un point associe la parité est continue et prend deux valeurs, paire pour l'extérieur et impaire pour l'intérieur. Jordan conclut (et c'est la partie difficile) que tout lacet simple est suffisamment proche d'un polygone pour que le résultat reste valable.
La preuve de Jordan est largement critiquée. Pour le mathématicien O. Veblen, la démonstration est vue comme : « l'étape la plus importante en direction d'une rigueur mathématique parfaite. », propriété qu'il n'accorde pas à la démonstration de Jordan et qui l'amène à en écrire une autre. Cette opinion est largement répandue. Deux mathématiciens, Courant et Robbins précisent « La démonstration de Jordan n'est ni courte ni simple, l'étonnement s'accroît lorsqu'il apparaît que sa preuve n'est pas valable et qu'il faut encore un effort considérable pour résoudre les lacunes laissées dans son raisonnement. ». L'objection majeure est que dans sa première édition de sa preuve (en 1887), les détails de la validité du théorème pour le polygone ne sont presque pas données, dans sa seconde édition (en 1893) ils sont expédiés en huit lignes et précisés uniquement sous la forme d'un exercice. Seule la partie véritablement difficile, à savoir la généralisation à tous les lacets simples, est explicitée. En 1996, un article reprenant les idées de Jordan est publié. Son auteur M. Reeken qualifie la preuve de Jordan comme « essentiellement valable ». Si la méthode de Jordan, à l'aide des polygones, est toujours d'actualité de par sa simplicité, celle de Veblen est tombée dans l'oubli.
Postérité du théorème
Dès sa naissance, le théorème de Jordan se trouve à la croisée de plusieurs branches des mathématiques. L'enjeu de Bolzano, c'est-à-dire de bâtir les mathématiques sur une base axiomatique et non pas sur des évidences intuitives, est toujours présent au début du XXe siècle. C'est dans le contexte d'une rigueur mathématique parfaite que Veblen est amené à reprendre les travaux de Jordan. Les travaux d'Henri Poincaré sur l'équation différentielle montre l'importance d'une meilleure compréhension des propriétés que l'on qualifie maintenant de topologiques et que Poincaré appelle analysis situ. La démonstration actuelle du théorème de Poincaré-Bendixson utilise explicitement le théorème de Jordan. Ce théorème est incontournable en analyse complexe à partir des années 1920. Constantin Carathéodory ne publie pas son livre sur ce sujet, car il ne parvient pas à trouver une preuve personnelle du théorème de l'article.
La branche naturelle du domaine du théorème reste néanmoins la topologie. Luitzen Brouwer cherche à établir les résultats fondamentaux de la topologie d'un espace euclidien, il généralise le résultat de Jordan à une dimension quelconque. Ce résultat est relativement intuitif en dimension trois : si une bouteille est hermétiquement fermée (ce qui revient à dire que la frontière du liquide contenu dans la bouteille peut se déformer continument) le liquide contenu à l'intérieur ne peut s'échapper. L'un des intérêts de la démonstration de Brouwer réside dans les méthodes utilisées, elles sont à l'origine de l'homologie, clé de la topologie algébrique moderne.
Le XXIe siècle n'est pas en reste avec le théorème de Jordan. Un enjeu moderne est la vérifiabilité d'une démonstration. Celle de Andrew Wiles pour le dernier théorème de Fermat demanda plus d'un an pour être nettoyée de toute erreur et acceptée par la communauté mathématique. Une technique consiste à élaborer une preuve formelle, vérifiable par ordinateur. En Janvier 2005, Thomas C. Hales apporte une preuve de cette nature.