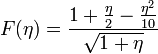Théorie des figures d'équilibre - Définition

Relation constitutive

Afin de rendre le problème d'une figure d'équilibre traitable, il faut se donner une loi rhéologique (ou relation constitutive) permettant d'exprimer le champ des tensions en termes de champs dérivés du champ des vitesses ou des déplacements. En général, on suppose que le comportement rhéologique à long-terme du milieu continu étudié est celui d'un fluide parfait. Alors, le tenseur des tensions T_ij est isotrope et peut se décrire au moyen d'un champ de pression scalaire p, soit

T_ij = − pδ_ij,

où δ représente le symbole de substitution de Kronecker : δ vaut 1 si i et j sont égaux, et 0 sinon.

Théorie du champ interne de Clairaut, Laplace et Lyapunov

Considérons la Terre comme un barotrope tournant à une vitesse angulaire uniforme ω autour de l'axe Ox₃. Nous désirons trouver sa forme d'équilibre pour une distribution de densité ρ spécifiée le long d'une direction inclinée d'un certain angle par rapport à l'axe de rotation. Sous le vocable « figure d'équilibre » nous ne comprenons pas seulement la forme de la surface externe et du champ de pesanteur externe, mais aussi la forme d'une strate interne quelconque, c'est-à-dire la forme de toutes les surfaces isopycniques, isobares et équipotentielles qui coïncident toutes dans le cas étudié ici. Nous prendrons l'origine O du système de référence au centre de masse de la Terre, et nous dénoterons par r le rayon vecteur qui joint l'origine à un point arbitraire situé sur une surface de niveau donnée

U(r,θ) = V(r,θ) + Z(r,θ) = Constant.

Comme il est coutumier, la lettre grecque θ (thêta) désigne la colatitude géocentrique, et r = |r| est la distance au centre de masse. En termes de coordonnées sphériques r, θ, λ le potentiel axifuge s'écrit

,

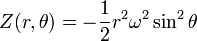
ou encore,

,

P désignant le polynôme de Legendre d'indice 2.

Les fonctions de figure

Pour un barotrope quelconque en rotation lente, et en particulier pour les modèles de Terre, les surfaces de niveau ne diffèrent que légèrement de la forme sphérique. Il est donc naturel, compte tenu des éléments de symétrie que doivent posséder ces surfaces, de rechercher l'équation décrivant la surface d'une couche quelconque sous la forme

.

La variable s désigne ici un paramètre judicieusement choisi devant permettre de reconnaître de quelle couche il s'agit — pour simplifier, on dira que s représente le nom de la couche considérée. Ainsi, on peut choisir s comme rayon équatorial a, ou comme rayon polaire c, de la couche en question. Dans la suite, nous choisissons s comme rayon équivolumétrique moyen de la couche, autrement dit, comme rayon de la sphère qui possède le même volume que celui contenu sous la couche.

De la sorte, le problème de trouver la forme d'équilibre est ramené au problème de déterminer un ensemble infini de fonctions s qu'on appelle les « fonctions de figure ». Afin de pouvoir utiliser la formule précédente en pratique, il est nécessaire que l'ordre de grandeur des fonctions de figure décroisse suffisamment vite avec l'ordre n pour assurer une convergence raisonnablement rapide de la série figurant dans le membre de droite. Pour les modèles de Terre en particulier, tel est bien le cas comme il sera montré plus loin.

Si nous tronquons la série à n = 1, nous sommes en présence de l'approximation du premier ordre qui correspond au cas classique de la théorie de Clairaut. Si nous tronquons la série à n = 2, nous obtenons l'approximation du second ordre qui correspond à la théorie de Darwin–de Sitter. Pour la Terre, l'approximation d'ordre 2 correspond à négliger des effets d'environ 10^-5 ; comme le rayon moyen de la Terre est de 6 371 km, on commet donc des erreurs qui peuvent se chiffrer typiquement à quelques mètres. De telles erreurs sont incompatibles avec la précision des mesures géodésiques atteinte à l'heure actuelle, qui est fournissent le rayon de la Terre à quelques centimètres près. Depuis la fin des années 1970, divers auteurs ont considéré pour le cas de la figure hydrostatique de la Terre des approximations d'ordre 3 et en ont fourni les formules appropriées. En réalité, pour autant qu'on ne désire pas faire des calculs effectifs, il n'est guère plus difficile de développer la théorie des figures d'équilibre à un ordre général n = N que de se limiter à l'ordre n = 2 ou n = 3, par exemple.

Théorie de Clairaut-Radau

Si nous négligeons les termes en ou plus petits, les équations de figure se réduisent à la seule équation

,

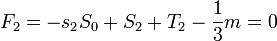
et l'aplatissement devient

.

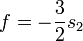
Combinant les deux, on obtient l'équation intégro-différentielle de Clairaut

.

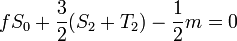
Les quantités S et T ne doivent être évaluées qu'à l'ordre , et S à l'ordre . Dès lors, avec x = s / s₁ et , on trouve

,

.

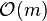
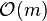
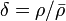
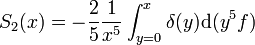
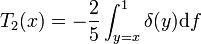
Équation différentielle de Clairaut

Sous cette forme, l'équation de Clairaut est une équation intégro-différentielle linéaire pour l'aplatissement des strates internes de la Terre. Elle peut être résolue itérativement par la méthode générale indiquée plus haut pour les fonctions de figure. Toutefois, l'approche classique consiste à dériver l'équation de de Clairaut sous la forme intégro-différentielle par rapport à x et éliminer les quantités m et T en faisant usage des deux dernières relations, obtenant ainsi

,

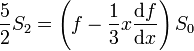
puis à multiplier ce résultat intermédiaire par x⁵ et dériver encore une fois par rapport à x. On obtient alors l'équation différentielle de Clairaut

.

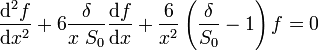
On peut intégrer numériquement cette dernière équation différentielle ordinaire en imposant que f reste fini en x = 0 (au centre) et que f satisfasse en x = 1 (à la surface) à la condition

.

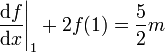
On aboutit à cette condition en multipliant l'équation intégro-différentielle de Clairaut ci-dessus par x⁵, en posant ensuite x = 1 et en notant que S₀(1) = 1.

Équation différentielle de Clairaut-Radau

Tout au long du XIX^e siècle, en l'absence des données fournies plus tard par la sismologie, les astronomes essayaient de déterminer la densité des couches internes de la Terre en imposant deux contraintes à diverses fonctions d'essai ρ = ρ(x) : (1) la fonction d'essai, par intégration sur le volume, devait fournir la valeur observée M de la masse de la Terre ; (2) en intégrant l'équation de Clairaut, la fonction d'essai devait fournir la valeur observée f de l'aplatissement géométrique en surface. Or, avant l'avènement des ordinateurs et, surtout, des microordinateurs personnels dans la deuxième moitié du XX^e siècle, la solution de l'équation différentielle de Clairaut s'obtenait par une intégration numérique qui devait se faire à la main et qui était fort fastidieuse.

Pour cette raison, l'élégante méthode de solution proposée en 1885 par l'astronome français d'origine prussienne Rodolphe Radau (1835–1911), qui simplifie énormément l'intégration de l'équation de Clairaut, devint la méthode de résolution standard et reste jusqu'à présent d'une grande valeur dans les travaux théoriques ayant recours à l'aplatissement calculé au premier ordre.

La méthode de Radau consiste à transformer l'équation de Clairaut en introduisant la fonction sans dimension dite « paramètre (ou variable) de Radau »

,

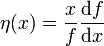
au moyen de laquelle on obtient l'équation de Clairaut-Radau

,

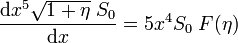
avec

.

Équation de Radau

Théorie de Darwin–de Sitter