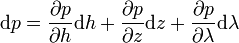Théorie des figures d'équilibre - Définition

Symétrie des figures d'équilibre

Lorsqu'on étudie la théorie des figures pour des corps cosmiques comme la Terre ou les planètes, c'est-à-dire pour des corps hétérogènes en rotation autour d'un axe polaire, la principale difficulté provient du fait qu'on ne peut pas admettre a priori une forme déterminée pour une surface de niveau, comme dans le cas de la théorie des figures d'équilibre des masses homogènes (par exemple, le sphéroïde de Maclaurin ou l'ellipsoïde de Jacobi) considérés en astronomie ou des ellipsoïdes de référence discutés en géodésie physique. Dès lors, l'examen des éléments de symétrie d'une figure d'équilibre permet de simplifier appréciablement la théorie. Dans la suite de cet article, nous allons considérer le cas de la Terre, mais la théorie générale s'applique aussi aux autres corps planétaires ainsi qu'aux étoiles simples.

Tout d'abord, nous supposons que la Terre est en rotation permanente, excluant ainsi de notre étude les phénomènes de marée ou des phénomènes électromagnétiques, par exemple. On a vu plus haut que sous ces conditions, le champ de vitesse angulaire et le champ de densité possèdent tous les deux une symétrie de révolution. Il s'ensuit que le potentiel gravifique d'un rotateur permanent possède lui-aussi la même symétrie axiale. Cette propriété de symétrie de peut être établie mathématiquement comme suit : soient (h, λ, z) et (h', λ', z') les coordonnées cylindriques du point potentié P et d'un point potentiant quelconque Q, respectivement. Les coordonnées cartésiennes correspondantes de P et Q, c'est-à-dire (x, x, x) et (x', x', x'), s'expriment au moyen des relations

,

.

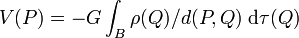
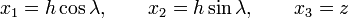
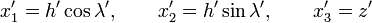
L'élément de volume en Q est , et la distance entre P et Q est

.

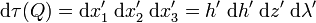
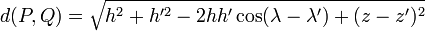
Comme ρ(Q) ne dépend pas de l'angle λ', l'intégration sur λ' dans l'expression de V(P) peut être remplacée par une intégration sur la différence λ' – λ avec les mêmes limites d'intégration 0 et 2π que pour λ'. De la sorte, la variable λ disparaît de l'intégrale, et

V = V(h,z)

ensemble avec

ρ = ρ(h,z)

et

ω = ω(h,z).

Principe de symétrie de Pierre Curie

En fait, la symétrie axiale de V aurait pu être déduite de la symétrie axiale de ρ en se servant du principe de symétrie établi par le physicien français Pierre Curie (1859–1906). Ce principe peut s'énoncer de façon concise comme suit : Tout effet produit par une cause déterminée doit posséder au moins les mêmes éléments de symétrie mais peut être plus symétrique que la cause. Toute dissymétrie rencontrée dans un effet donné doit aussi exister dans la cause qui a produit l'effet. En corollaire, s'il existe une relation de réciprocité entre une cause et un effet, dans le sens que la cause peut tout aussi bien être considérée comme l'effet, et l'effet comme la cause, les deux — cause et effet — doivent posséder exactement les mêmes éléments de symétrie. Un exemple de ce cas est fourni par une relation entre les tensions et les déformations, à savoir ce que nous avons appelé plus haut une « relation constitutive ». Il semble que l'on n'ait pas encore trouvé jusqu'à présent d'expérience ni d'observation se rapportant à des phénomènes macrophysiques qui contredise le principe de Curie, et ce dernier devrait être considéré comme une loi universelle de la Nature au même titre que les lois de la thermodynamique, par exemple. Nous allons adopter ce point de vue ici pour déduire certaines propriétés des figures d'équilibre.

Tout d'abord, nous notons que la force d'attraction gravifique est centrale, et possède donc le plus haut degré de symétrie, celui de la sphère. Le principe de Curie requiert alors que l'arrangement des masses produit par la seule action de l'attraction gravifique doit correspondre à la symétrie sphérique : une quelconque configuration moins symétrique est exclue si l'on veut avoir équilibre. Une preuve mathématique du fait que la sphère est l'unique figure d'équilibre possible d'un corps fluide isolé au repos fut donnée par Lyapunov en 1884.

Ensuite, considérons l'action combinée d'une force d'attraction gravifique et d'une force axifuge. Cette dernière introduit une certaine asymétrie par rapport à la sphère par le fait que la force axifuge possède la symétrie d'un cylindre de révolution. Le principe de Curie requiert donc que la distribution d'équilibre des masses possède la même symétrie axiale, puisqu'il existe une relation de réciprocité entre la distribution de densité et le potentiel. C'est le cas étudié plus haut en termes mathématiques.

Équation d'état : barotropes et baroclines

Un point particulier doit retenir toute notre attention à ce stade. En effet, afin de compléter la formulation du problème, nous devons inclure une équation d'état appropriée. Sous forme générale, celle-ci peut s'écrire

.

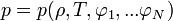
La lettre p désigne la pression, ρ est la densité, T est la température, et l'ensemble des variables φ à φ décrit la composition chimique et minéralogique. Par définition, une structure baroclinique (ou, simplement, un barocline) est un système pour lequel une relation physique de cette forme existe. Toutefois, dans certaines circonstances spéciales qui sont approximativement remplies dans le cas de l'intérieur de la Terre, la pression peut simplement être reliée à la densité, à savoir

p = p(ρ).

Si tel est le cas, on dira qu'il s'agit d'une équation d'état barotropique et la structure correspondante est un barotrope. En première approximation, nous pouvons considérer la Terre comme un barotrope.

La distinction fondamentale entre modèles barotropiques et modèles barocliniques se trouve dans leurs stratifications respectives. Il est clair que les surfaces d'égale densité (surfaces isopycniques) et les surfaces d'égale pression (surfaces isobares) coïncident dans un barotrope. Par contre, dans les baroclines les surfaces d'égale densité coupent les surfaces d'égale pression, à moins que des conditions très spécifiques ne soient remplies.

Tenant compte de la symétrie axiale de ρ et V, l'équation de mouvement d'un rotateur permanent devient en coordonnées cylindriques

,

,

.

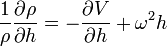
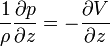
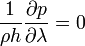
Le fait que ∂p/∂λ = 0 établit la symétrie de révolution du champ de pression, c'est-à-dire

p = p(h,z).

Équilibre hydrostatique relatif

On définit les composantes de la pesanteur en coordonnées cylindriques par les relations

,

,

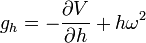
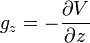
g_λ = 0.

Dès lors, dans un corps en rotation permanente, la pesanteur est partout orthogonale aux isobares, comme on le constate en se souvenant de la définition du gradient. Constatons que cette propriété est très générale : elle est valable tout aussi bien pour les baroclines que pour les barotropes, et qu'elle est valable pour une rotation uniforme comme pour une rotation différentielle, pour autant que le champ de vitesse angulaire conserve une symétrie axiale. En général, on définit le potentiel axifuge comme

,

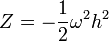
mais il est évident que cette définition n'est valable que pour une rotation uniforme. Si tel est le cas, nous pouvons employer un système d'axes fixé dans le corps et tournant avec lui. Si chaque particule du corps est au repos par rapport à ce référentiel qui n'est pas d'inertie, on dit que le corps est en équilibre hydrostatique relatif ou, plus simplement, en équilibre hydrostatique. Le plus souvent, dans les théories géodésiques ou géophysiques, on admet que tel est le cas pour la Terre.

Au contraire, si la vitesse angulaire n'est pas constante d'un point à l'autre, il ne peut exister qu'un équilibre hydrodynamique. Une rotation différentielle de ce type joue probablement un rôle important dans les étoiles et les planètes géantes, mais semble exclue dans les planètes telluriques à cause d'un trop fort couplage visqueux ou électromagnétique entre les différentes strates. Les études des figures d'équilibre générales donnent souvent le plus d'importance à la rotation zonale, que l'on nomme circulation méridienne ou courants de von Zeipel, ou courants d'Eddington, ou encore courants de Jardetzky. Toutefois, l'étude des courants de convection ne fait généralement pas partie de la théorie des figures d'équilibre.

Théorème de Wavre-Poincaré

Les relations ci-dessus définissant les composantes de la pesanteur montrent qu'un potentiel axifuge Z, et donc une surface de niveau

U = V + Z = Constante

peut exister si et seulement si ω ne dépend pas de z, c'est-à-dire si la vitesse angulaire est constante sur des surfaces cylindriques centrées sur l'axe de rotation, autrement dit si ω = ω(h). Dans ce cas plus général que la rotation uniforme, on définit le potentiel axifuge par

.

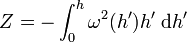
Nous constatons, en particulier, que pour une rotation uniforme, cette relation se réduit bien à la relation précédente comme il se doit.

Une conclusion importante qu'on peut tirer de l'existence d'un potentiel de rotation, et donc de l'existence d'un potentiel de pesanteur, est

,

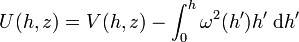
de sorte que

,

,

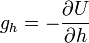
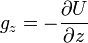
g_λ = 0.

On donne à cette conclusion souvent le nom de théorème de Wavre-Poincaré, et on peut l'énoncer sous la forme suivante : Pour un rotateur permanent, l'une quelconque des propriétés qui suivent entraînent automatiquement les trois autres, à savoir

1. la vitesse angulaire est constante sur des cylindres centrés sur l'axe de rotation ;
2. la pesanteur dérive d'un potentiel ;
3. la pesanteur est normal aux surfaces d'égale densité ;
4. les surfaces d'égale densité coïncident avec les surfaces d'égale pression.. En effet, selon les équations pour le gradient de la pression et pour les composantes de la pesanteur fournies plus haut, on peut écrire pour la différentielle totale

l'équation suivante :

,

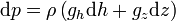
donc

.

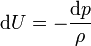
Un déplacement arbitraire sur une surface de niveau fournit dU = 0, impliquant donc que dp = 0. Les surfaces isobares coïncident donc avec les surfaces de niveau, et p = p(U) ou U = U(p). Nous trouvons ainsi à cause de la relation sur dU que la densité est aussi constante sur surface de niveau. En conclusion, les isobares, les isopycniques et les surfaces de niveau coïncident toutes s'il existe un potentiel de pesanteur, et la force par unité de masse due à la pesanteur est normale à ces surfaces. En particulier, elle est normale aux isopycniques. Réciproquement, considérons un corps pour lequel les isobares et les isopycniques coïncident. On peut alors définir une fonction U(p), en termes de laquelle la relation donnant la différentielle de la pression devient

dU = − g_hdh − g_zdz,

montrant que dU est une différentielle totale exacte. Par conséquent, les relations g_h(h,z) = – ∂U/∂h, g_z(h,z) = – ∂U/∂z, g_λ(h,z) = 0 doivent s'appliquer, et le champ de pesanteur dérive d'un potentiel. Finalement, supposons que la pesanteur est partout normale aux surfaces d'égale densité, soit gx∇ρ = 0. Comme g = – ∇U = ρ^–1 ∇p, la coïncidence des surfaces isobares et isopycniques est établie, et tous les énoncés du théorème de Wavre-Poincaré sont démontrés.

Baroclines et pseudo-barotropes

Il est important de se rendre compte que la condition ω = ω(h), ou la condition équivalente ∂ω/∂z = 0, ne requiert aucune connaissance préalable de l'équation d'état. Selon le théorème de Wavre-Poincaré, les isopycniques d'un barocline coïncideront donc avec ses isobares si ∂ω/∂z = 0. Toutefois, il est évident que de tels baroclines particuliers devraient être appelés de façon plus appropriée des pseudo-barotropes, parce qu'ils partagent la plupart de leurs propriétés avec les barotropes véritables, et se distinguent clairement des baroclines véritables.

Cette constatation nous permet de revenir aux considérations de symétrie. Tout d'abord, le principe de Curie nous apprend que les barotropes sont au moins aussi symétriques que les baroclines véritables, mais peuvent être plus symétriques.

Théorème de Lichtenstein

Le principe de Curie (sans symétrie brisée) permet d'inférer une autre propriété de symétrie très importante des figures d'équilibre : un quelconque rotateur permanent barotropique ou pseudo-barotropique doit posséder un élément de symétrie supplémentaire, à savoir un plan équatorial, c'est-à-dire un plan normal à l'axe de rotation qui passe par le centre de masse. Cet énoncé constitue le théorème de Lichtenstein.

Mais cette preuve physique du théorème de Lichtenstein dans toute sa généralité exigerait l'unicité de solution, et la démonstration mathématique rigoureuse n'est pas triviale du tout.

Le cas d'un barocline véritable est quelque peu plus compliqué, mais Dive a démontré en 1930 qu'un barocline en rotation différentielle est symétrique par rapport à un plan équatorial si la vitesse angulaire est partout une fonction biunivoque de la densité et de la distance à l'axe de rotation.