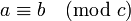Théorie des nombres - Définition

Citation

La mathématique est la reine des sciences et la théorie des nombres est la reine des mathématiques. Gauss

Histoire de la théorie des nombres

Civilisation védique

Les mathématiciens de l'Inde se sont intéressés à la recherche de solutions intégrales solutions d'équations diophantiennes depuis la période védique. L'usage géométrique le plus ancien des équations diophantiennes peut être retracé dans les Sulba Sutras, qui ont été écrits entre le VIII^e et le VI^e siècle av. J.-C. Baudhayana (env. 800 avant JC) trouva deux ensembles de solutions intégrales positives à un système d'équations diophantiennes, et utilisa aussi les systèmes d'équations diophantiennes à quatre inconnues. Apastamba (env. 600 avant JC) utilisa les systèmes d'équations diophantiennes à cinq inconnues.

Époque jaïna

En Inde, les mathématiciens de l'époque jaïna développèrent une théorie des nombres systématique du IV^e siècle av. J.-C. jusqu'au II^e siècle av. J.-C. Le texte Surya Prajinapti (env. 400 avant JC) classe tous les nombres en trois ensembles : énumérables, non énumérables et infini. Chacun de ces trois ensembles était divisé plus avant en trois ordres :

• Énumérables : le plus bas, intermédiaire et le plus haut.
• Non énumérable : non énumérable proche, vraiment non énumérable et non énumérablement non énumérable.
• Infini : infini proche, vraiment infini, infiniment infini.

Les mathématiciens de l'époque jaïna furent les premiers à écarter l'idée que tous les infinis sont les mêmes ou égaux. Ils reconnurent cinq types différents d'infini : infini dans une ou deux directions (une dimension), infini en surface (deux dimensions), infini partout (trois dimensions), et infini perpétuellement (dans un nombre infini de dimensions).

Le nombre énumérable le plus haut N des ouvrages jaïnas correspond au concept moderne de aleph-zéro (le nombre cardinal de l'ensemble infini des entiers 1, 2, ...), le plus petit nombre transfini cardinal. Les mathématiciens de cette époque ont défini aussi un système entier de nombres cardinaux transfinis, dans lequel notre est le plus petit.

Dans le travail sur la théorie des ensembles, deux types de nombres transfinis de base ont été distingués. Pour des raisons à la fois physiques et ontologiques, une distinction fut faite entre asmkhyata et ananata, entre infini rigidement lié et infini pauvrement lié.

Civilisation grecque

La théorie des nombres fut une étude favorite parmi les mathématiciens grecs d'Alexandrie, Égypte à partir du III^e siècle av. J.-C., qui eurent conscience du concept d'équation diophantienne dans de nombreux cas particuliers. Le premier mathématicien hellène à étudier ces équations fut Diophante.

Diophante a également recherché une méthode pour trouver les solution entières pour les équations indéterminées linéaires, équations pour lesquelles il manque une information suffisante pour produire un ensemble unique de réponses discrètes. L'équation est une telle équation. Diophante a découvert que beaucoup d'équations indéterminées peuvent être ramenées à une forme où une certaine catégorie de solutions est connue alors qu'une solution spécifique ne l'est pas.

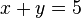
L'époque classique en Inde

Les équations diophantiennes furent étudiées de manière intensive par les mathématiciens indiens de la période médiévale, qui furent les premiers à chercher systématiquement des méthodes pour la détermination de solutions intégrales d'équations diophantiennes. Aryabhata (en 499) donna la première description explicite de la solution intégrale générale de l'équation diophantienne linéaire , qui apparaît dans son texte Aryabhatiya. Cet algorithme kuttaka est considéré comme étant l'une des contributions les plus significatives d'Aryabhata en mathématiques pures, qui trouva les solutions d'équations diophantiennes en termes de fractions continues. La technique fut appliquée par Aryabhata pour donner les solutions intégrales d'un système d'équations diophantiennes linéaires, un problème avec d'importantes applications en astronomie. Il trouva aussi la solution générale de l'équation linéaire indéterminée en utilisant cette méthode.

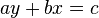
Brahmagupta en 628 manipula des équations diophantiennes plus difficiles. Il utilisa la méthode chakravala pour résoudre les équations diophantiennes quadratiques, incluant des formes de l'équation de Pell-Fermat, telle que . Son Brahma Sphuta Siddhanta fut traduit en arabe en 773 et fut traduit plus tard en Latin en 1126. L'équation fut plus tard posée comme un problème en 1657 par le mathématicien français Pierre de Fermat. La solution générale de cette forme particulière d'équation de Pell-Fermat fut trouvée plus de 70 ans plus tard par Leonhard Euler, tandis que la solution générale de l'équation de Pell-Fermat fut trouvée plus de 100 ans plus tard par Joseph Louis Lagrange en 1767. En attendant, il y a beaucoup de siècles de cela, la solution générale de l'équation de Pell-Fermat fut enregistrée par Bhaskara II en 1150, utilisant une version modifiée de la méthode chakravala de Brahmagupta, qu'il utilisa aussi pour trouver la solution générale d'autres équations quadratiques intermédiaires indéterminées et des équations diophantiennes quadratiques. La méthode chakravala de Bhaskara pour trouver la solution générale de l'équation de Pell-Fermat était plus simple que la méthode utilisée par Lagrange 600 ans plus tard. Bhaskara trouva aussi des solutions pour d'autres équations indéterminées quadratiques, cubique, quartique et des équations polynômiales de degré plus élevés. Narayana Pandit perfectionna encore la méthode chakravala et trouva plus de solutions générales pour les autres indéterminées quadratiques ainsi que pour les équations polynômiales de degré plus élevés.

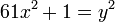
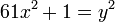
La civilisation islamique

À partir du IX^e siècle, les mathématiciens islamiques portèrent un vif intérêt a la théorie des nombres. Le premier de ces mathématiciens fut le mathématicien arabe Thabit ibn Qurra, qui découvrit un théorème qui permettait de trouver des paires de nombres amiables, c’est-à-dire deux nombres qui sont chacun la somme des diviseurs propres de l'autre.

Au X^e siècle, Al-Baghdadi découvrit une légère variante du théorème de Thabit ibn Qurra. Al-Haitham semble avoir été le premier à tenter de classer tous les nombres parfaits pairs (nombres égaux à la somme de leurs diviseurs propres) comme ceux de la forme où est premier. Al-Haytham est aussi la première personne à avoir établi le théorème de Wilson, concrètement que si p est premier alors est divisible par . Le fait n'est pas éclairci s'il savait comment démontrer ce résultat. Ce théorème porte le nom de théorème de Wilson à cause d'un commentaire fait par Edward Waring en 1770 dont John Wilson avait noté le résultat. John Wilson indique à Waring qu'il ne sait pas démontrer ce résultat, Waring ne trouve pas non plus de preuve. Pourtant la première démonstration connue provient de Leibniz, qui ne juge pas utile de la publier, et Euler en avait publié une preuve.

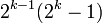
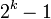
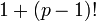
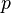
Les nombres amiables ont joué un grand rôle dans les mathématiques islamiques. Au XIII^e siècle, le mathématicien perse Al-Farisi donna une nouvelle démonstration du théorème de Thabit ibn Qurra, introduisant de nouvelles idées concernant la décomposition et les méthodes combinatoires. Il donna aussi la paire de nombre amiables 17 296, 18 416 qui ont été attribués à Euler, mais nous savons que ceux-ci étaient connus plus tôt que Al-Farisi, peut-être même par Thabit ibn Qurra lui-même. Au XVII^e siècle, Muhammad Baqir Yazdi donna la paire de nombres amiables 9 363 584 et 9 437 056 toujours bien avant avant la contribution d'Euler.

Début de la théorie des nombres en Europe

La théorie des nombres en Europe commence aux XVIe et XVIIe siècles par les travaux de Viète, Bachet de Méziriac et surtout Fermat. Au XVIII^e siècle, Euler et Lagrange contribuèrent à la théorie, vers la fin du siècle, le sujet commence à prendre une forme scientifique à travers les grands travaux de Legendre (1798) et Gauss (1801). Avec ce dernier et son ouvrage, les Disquisitiones arithmeticae (1801), on peut dire que la théorie moderne des nombres commence.

Tchebychev (1850) donna des limites très utilisées pour les nombres premiers entre deux nombres donnés. Riemann (1859) conjectura que la limite de la densité des nombres premiers n'excède pas une fonction donnée (le théorème des nombres premiers), introduisit l'analyse complexe dans la théorie de la fonction ζ de Riemann, et en déduisit la formule des nombres premiers à partir de ses zéros.

L'arithmétique modulaire a réellement débuté avec les Disquisitiones arithmeticae de Gauss. Il introduisit le symbolisme suivant :

et explora la plus grande partie de ce domaine. Il généralise la théorie à d'autres anneaux de celui des entiers relatifs et découvre le premier ensemble d'entiers algébriques : les entiers de Gauss. Tchebychev publia en 1847 un travail en russe sur le sujet, et en France Serret le popularisa.

A côté du travail résumé précédemment, Legendre établit les premiers cas d'application loi de réciprocité quadratique. Cette loi, découverte par induction et énoncée par Euler, fut prouvée en premier par Legendre dans sa Théorie des Nombres (1798) pour des cas exceptionnels. Indépendamment d'Euler et Legendre, Gauss découvrit la loi vers 1795, et fut le premier à en donner une preuve générale. Au sujet contribuèrent aussi : Cauchy ; Dirichlet son Vorlesungen über Zahlentheorie est un classique ; Jacobi, qui introduisit le symbole de Jacobi ; Liouville, Zeller (?), Eisenstein, Kummer, et Kronecker. La théorie s'étendit pour inclure la réciprocité biquadratique et cubique, (Gauss, Jacobi qui fut le premier à prouver la loi de réciprocité cubique, et Kummer).

On doit aussi à Gauss la représentation des nombres par des formes quadratiques binaires. Cauchy, Poinsot (1845), Lebesgue (?) (1859, 1868), et notablement Hermite ont contribué à ce sujet. Dans la théorie des formes ternaires, Eisenstein a été un chef de file, et grâce à lui et aussi à H. J. S. Smith, on doit une avancée remarquable dans la théorie des formes en général. Smith donna une classification complète des formes quadratiques ternaires, et étendit les recherches de Gauss concernant les formes quadratiques réelles vers les formes complexes. Les recherches concernant la représentation des nombres par la somme de 4, 5, 6, 7, 8 carrés furent approfondies par Eisenstein et la théorie fut complétée par Smith.

Dans l'histoire de la théorie des nombres, le dernier théorème de Fermat joue un rôle à part, en raison des efforts considérables, étalés sur plus de trois cents ans, des mathématiciens du monde entier pour en apporter la preuve (ou la négation). Ce théorème affirme que pour n > 2, il n'existe pas d'entiers non nuls x, y et z vérifiant :

.

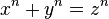
Pierre de Fermat lui-même en apporta la preuve dans le cas particulier n = 4. Euler, en 1753, le démontra presque pour n = 3, introduisant dans sa preuve les nombres imaginaires. En 1825, Dirichlet et Legendre démontrent le cas n = 5, en utilisant une avancée décisive de la française Sophie Germain (cf Démonstrations du dernier théorème de Fermat). Lamé résout le cas n = 7 en 1839. Ces différents cas sont résolus à l'aide de structure d'anneaux euclidien de la même nature que les entiers de Gauss, ce sont les anneau d'entiers d'Eisenstein et d'entiers de Dirichlet. Kummer en 1847 prouve le théorème lorsque l'exposant n est un nombre premier régulier, et ouvre la théorie de idéaux. À la fin du XIX^e et au début du XX^e siècle, les mathématiciens délaissent le grand théorème de Fermat pour se consacrer aux fondements des mathématiques. En 1955, le japonais Taniyama émet l'hypothèse d'un lien profond entre les courbes elliptiques rationnelles et les formes modulaires, deux domaines a priori très éloignés des mathématiques. Ribet, prouvant une conjecture de Serre, montre que cette conjecture de Shimura-Taniyama-Weil a pour conséquence le grand théorème de Fermat. C'est Andrew Wiles qui prouvera une portion suffisante de cette conjecture en 1994, avec l'aide de Richard Taylor, et apportera une réponse définitive au célèbre problème.

Parmi les derniers auteurs français se trouvent Borel, Poincaré (leurs mémoires sont nombreux et de grande valeur), Tannery, et Stieltjes. Parmi les plus grands contributeurs en Allemagne se trouvent Kronecker, Kummer, Schering, Bachmann, et Dedekind. En Autriche, le travail de Stolz Vorlesungen über allgemeine Arithmetik (1885-1886), et en Angleterre George B. Mathews, sa 'Théorie des nombres (Part I, 1892)' est l'un des plus érudits des travaux généraux. Genocchi, Sylvester, et Glaisher ont aussi participé à la théorie.