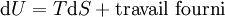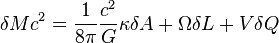Thermodynamique des trous noirs - Définition

Interprétation statistique

Une question ouverte dans le domaine de la thermodynamique des trous noirs est celui de l'interprétation de l'entropie des trous noirs. Il apparaît vraisemblable qu'une théorie de la gravitation quantique viable sera en mesure de donner une interprétation de l'entropie associée aux trous noirs en termes de micro-états. À l'heure actuelle, la théorie des cordes a été en mesure de proposer une telle interprétation pour certaines classes de trous noirs extrémaux, les autres types de trous noirs étant pour l'heure trop complexes pour être décrits au niveau quantique par la théorie des cordes. La gravité quantique à boucles propose également une interprétation de l'entropie, mais pour un trou noir de Schwarzschild seulement. Il n'est cependant pas clair que le raisonnement utilisé puisse être étendu de façon cohérente pour d'autres types de trou noir.

Les lois de la thermodynamique des trous noirs

Les résultats précédents permirent de reformuler l'ensemble des lois de la thermodynamique dans le contexte des trous noirs :

Loi	Thermodynamique ordinaire	Trous noirs
Principe zéro	La température T d'un corps est la même partout dans celui-ci à l'équilibre thermique	La gravité de surface κ est constante sur toute la surface du trou noir
Premier principe
Second principe	δ S est positif dans toute transformation impliquant un système fermé	δ A est positive dans toute transformation impliquant des trous noirs
Troisième principe	Impossibilité d'obtenir T = 0 par un processus physique	Impossibilité d'obtenir κ = 0 (trou noir extrémal) par un processus physique.

Le principe zéro est une conséquence immédiate des propriétés de la gravité de surface, qui comme son nom le suggère est constante sur toute la surface d'un trou noir. Ce résultat est en lui même peu intuitif car pour une planète en rotation, l'intensité du champ gravitationnel est moindre à l'équateur qu'aux pôles en raison de la force centrifuge. Néanmoins, les trous noirs ne présentent pas un tel effet, et l'intensité du champ gravitationnel (ou plus précisément la vitesse à laquelle celui-ci diverge quand on s'approche de la surface) est constante.

Le troisième principe appliqué au cadre des trous noirs stipule lui qu'on ne peut atteindre l'état de trou noir dit extrémal, c'est-à-dire la frontière entre trou noir et singularité nue. Par exemple, en augmentant la charge électrique d'un trou noir, on peut envisager de faire disparaître son horizon. Néanmoins, l'énergie à fournir aux particules chargées que l'on doit alors envoyer vers le trou noir de même charge devient de plus en plus grande quand on s'approche de l'état extrémal. De plus, un phénomène de type création de paires particules-antiparticules dans le voisinage du trou noir aura tendance à fabriquer des paires dont celles ayant une charge électrique opposée à celle du trou noir étant absorbées par celui-ci, et les autres étant repoussées par son champ électrique.

La formalisation des principes de la thermodynamique des trous noirs a été formulée en 1973 par James M. Bardeen (le fils du double Prix Nobel de physique John Bardeen), Brandon Carter et Stephen Hawking, avant même la découverte de l'entropie des trous noirs par Hawking deux ans plus tard.

Développements ultérieurs

L'application des techniques de la thermodynamique aux trous noirs permet de mettre en évidence tout un ensemble de phénomènes riches avec les trous noirs. En particulier, il est possible de calculer la chaleur spécifique des trous noirs. Le physicien australien Paul C. W. Davies a montré en 1977 que cette chaleur spécifique divergeait comme 1 / (T − T_c) pour certaines configurations atteignant une certaine température critique T_c dépendant des paramètres du trou noir. Un tel comportement est habituellement interprété en termes de transition de phase du second ordre. Il semble donc vraisemblable d'envisager que de tels phénomènes seront présents dans l'interprétation microscopique de l'entropie des trous noirs.