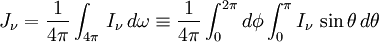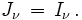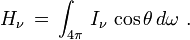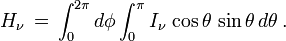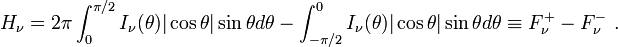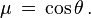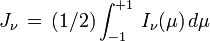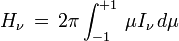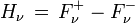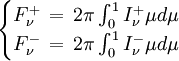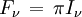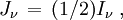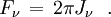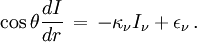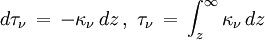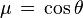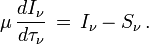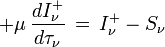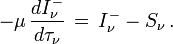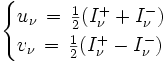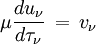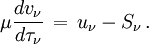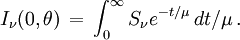Transfert de rayonnement - Définition

Moments de l'intensité

L'intensité caractérise l'énergie traversant une surface dans une direction. L'intégration de cette intensité sur les angles avec pondération par une certaine puissance du cosinus μ de la direction angulaire conduit à la définition de grandeurs physiques importantes et significatives.

L’intensité moyenne est la moyenne de l'intensité sur tout l'angle solide et s'exprime donc sous la forme

Si le rayonnement est isotrope (I ne dépend pas de l'angle, ce qui peut être valable dans des couches profondes de l'étoile), on a évidemment

Le flux à travers une surface est le moment d'ordre 1 de l'intensité, c'est-à-dire la quantité

Physiquement, H représente le flux d'énergie traversant une surface donnée perpendiculaire à un rayon issu du centre de l'étoile. En effet, si on considère cette surface élémentaire dS, la quantité d'énergie du faisceau le traversant dans la direction θ sera proportionnelle à cosθ selon la formule définissant l'intensité. Le flux est donc

Comme le cosinus change de signe lorsque l'angle θ varie entre 0 et π, on voit que le flux est en réalité, physiquement parlant, la différence entre deux quantités : le flux d'énergie correspondant aux rayons lumineux dirigés vers l'extérieur de l'étoile et le flux des rayons dirigés vers l'intérieur de l'étoile. Autrement dit (on suppose d'ordinaire que l'intensité ne dépend pas de l'azimut φ)

Il est d'usage en astrophysique de poser

Avec cette notation l'intensité moyenne devient

et le flux,

ou encore

avec

en distinguant entre un faisceau sortant I⁺ et un faisceau entrant I ^-.

Si on se place à la surface d'une étoile et si on suppose que l'intensité émergente ne dépend pas de la direction du faisceau (ce qui est d'ailleurs faux en général) et qu'il n'y a pas d'intensité rentrante (ce qui en revanche est vrai en général) on a

et

ce qui signifie que

Géométrie plan-parallèle

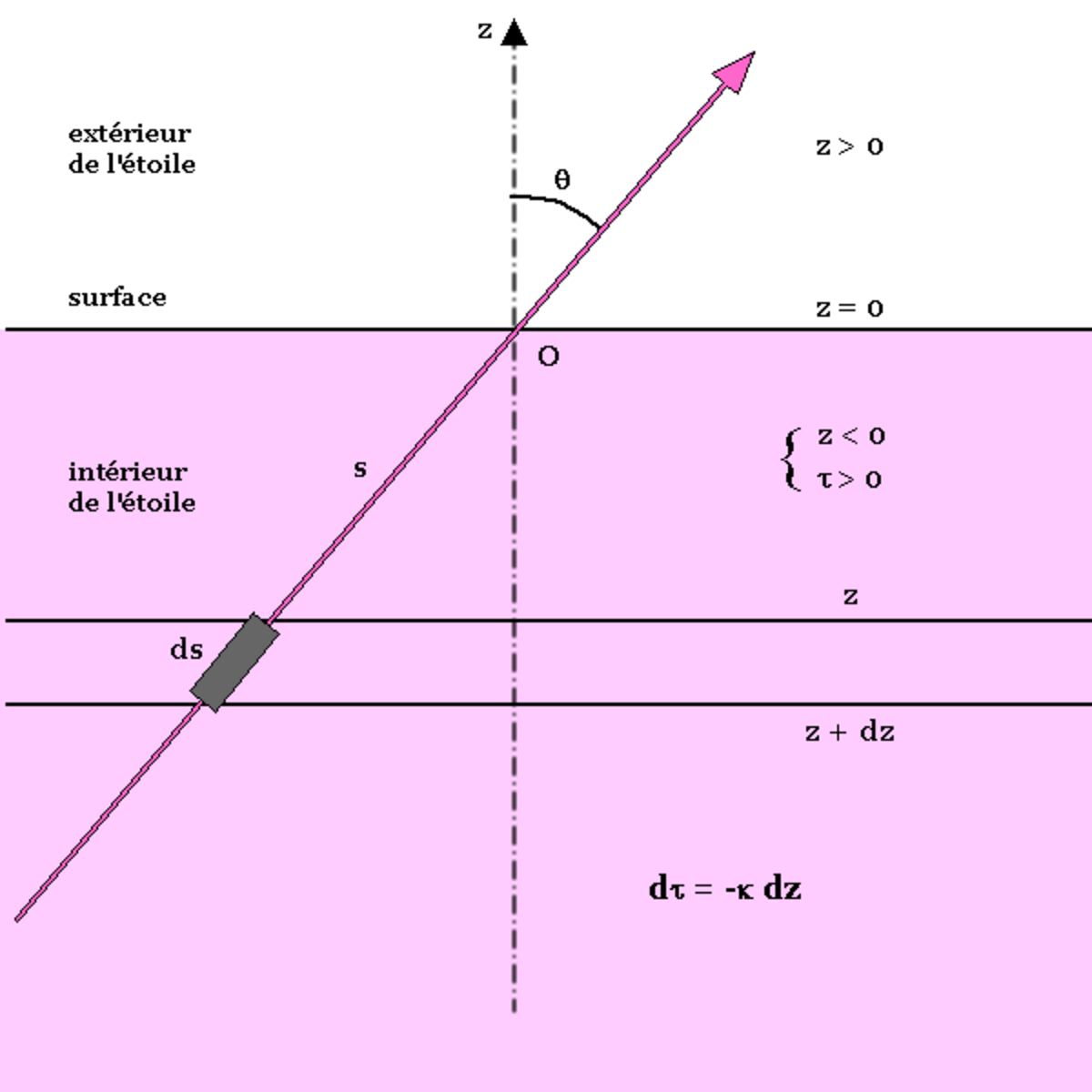
On utilise très souvent l'approximation dite « plan-parallèle » dans laquelle la courbure des couches de l'étoile est négligée. Cette approximation est valable si la largeur géométrique des couches considérées est petite devant la distance de ces couches au centre de l'étoile. Elle n'est pas valable pour des atmosphères étendues, un terme qui désigne les couches extérieures très diluées d'étoiles de grande taille, comme les géantes ou les supergéantes. Dans les équations du cas sphérique, il suffit de faire tendre r vers l'infini pour tomber sur l'équation de transfert plan-parallèle suivante :

En définissant la profondeur optique τ le long de la normale aux couches selon les conventions précisées sur la figure par

(τ est nul pour z infini, c'est-à-dire à l'observateur) et en notant à nouveau

on obtient l'équation de transfert sous la forme usuelle

Il est utile à la fois du point de vue numérique et physique de distinguer entre intensité émergente I ⁺ et intensité entrante I ^-. Avec cette convention l'angle θ entre la normale à la couche et le rayon lumineux varie seulement entre 0 et π/2 et μ reste positif entre 0 et 1. On écrit

En introduisant les nouvelles variables u et v définies par

qui ont respectivement le caractère d'une intensité moyenne et d'un flux, on obtient le système :

C'est sur ce système d'équations que se basent toutes les méthodes différentielles de résolution numérique du transfert car, étant physiquement pertinent, il se révèle plus stable que l'équation de transfert sur I.

À la surface de l'étoile le rayonnement émergent suivant l'angle θ donné par son cosinus μ = cosθ s'exprime sous la forme :

Cette formule a un caractère très général. Elle permet de calculer directement l'intensité sortant d'une étoile si on connaît la fonction source du rayonnement en tout point de son atmosphère.