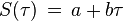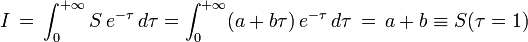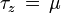Transfert de rayonnement - Définition
La liste des auteurs de cet article est disponible ici.
Approximations
Équilibre thermodynamique local
Une approximation utilisée très souvent en astrophysique est celle de l’équilibre thermodynamique local (ETL en français, LTE en anglais). Elle consiste à supposer que la fonction source du rayonnement est égale à la fonction de Planck, soit
Cette hypothèse revient à supposer que les populations des différents niveaux des atomes susceptibles d'émettre le rayonnement suivent la loi de Boltzmann, autrement dit que les atomes sont peuplés comme si l'équilibre thermodynamique régnait. Toute la subtilité du transfert réside en ce que si la fonction source est égale à la fonction de Planck, on ne peut pas en dire autant de l'intensité du rayonnement.
Approximations de diffusion
Les écarts à l'équilibre thermodynamique, qui se traduisent en particulier par le fait que l'intensité du rayonnement n'est pas égale à la fonction de Planck, sont intimement liés à la non-isotropie du rayonnement. Puisqu'un flux de lumière est transporté vers l'extérieur, c'est le signe que sur le bilan global l'intensité sortante doit être supérieure à l'intensité rentrante. L'équation de transfert nous permet de calculer cet effet. Pour fixer les idées nous nous placerons à l'ETL (équilibre thermodynamique local).
Dans les couches les plus profondes d'une étoile le rayonnement est emprisonné, se met de ce fait en équilibre avec la matière et devient lui aussi égal à la fonction de Planck. Mais cela n'est pas tout à fait vrai, autrement aucun rayonnement ne sortirait de l'étoile. L'approximation de diffusion consiste à développer la fonction source en fonction de la profondeur optique dans l'atmosphère autour du point τ selon la formule
L'intégration de l'équation de transfert fournit alors les résultats
Ne conserver dans ces expressions que les termes écrits revient à faire l'approximation de diffusion. Cette approximation a une grande importance historique car elle a permis de traiter des problèmes de transfert dans les atmosphères stellaires avant l'avènement de l'informatique. L’approximation d'Eddington est l'une des plus célèbres. Elle consiste à écrire que partout dans l'atmosphère
Dans ce que l'on appelle en astrophysique le cas gris, le coefficient d'absorption est pris comme constant sur les fréquences (ce qui n'est jamais réalisé d'ailleurs). On peut alors intégrer les équations précédentes sur les fréquences. Comme
où σ est la constante de Stefan-Boltzmann et T la température du corps noir. Il résulte de ce qui précède que dans l'approximation d'Eddington la quantité T 4 est une fonction linéaire de la profondeur optique τ, plus précisément
où T représente la température du gaz à la surface de l'étoile.
Relation de Barbier-Eddington
Supposons que la fonction source S soit une fonction linéaire
de la profondeur optique τ comptée le long de la ligne de visée. L'intégration de l'équation de transfert fournit pour l'intensité émergente de l'étoile la valeur
d'après des formules classiques.
En d'autres termes l'intensité I le long d'une ligne de visée est égale à la fonction source au point de cette ligne de visée situé à la distance optique unité. On résume rapidement ce fait en disant que l'intensité reflète la fonction source à la profondeur optique τ = 1. Ce résultat constitue l'approximation connue sous le nom de relation de Barbier-Eddington, une relation utilisée très souvent pour raisonner en ordre de grandeur.
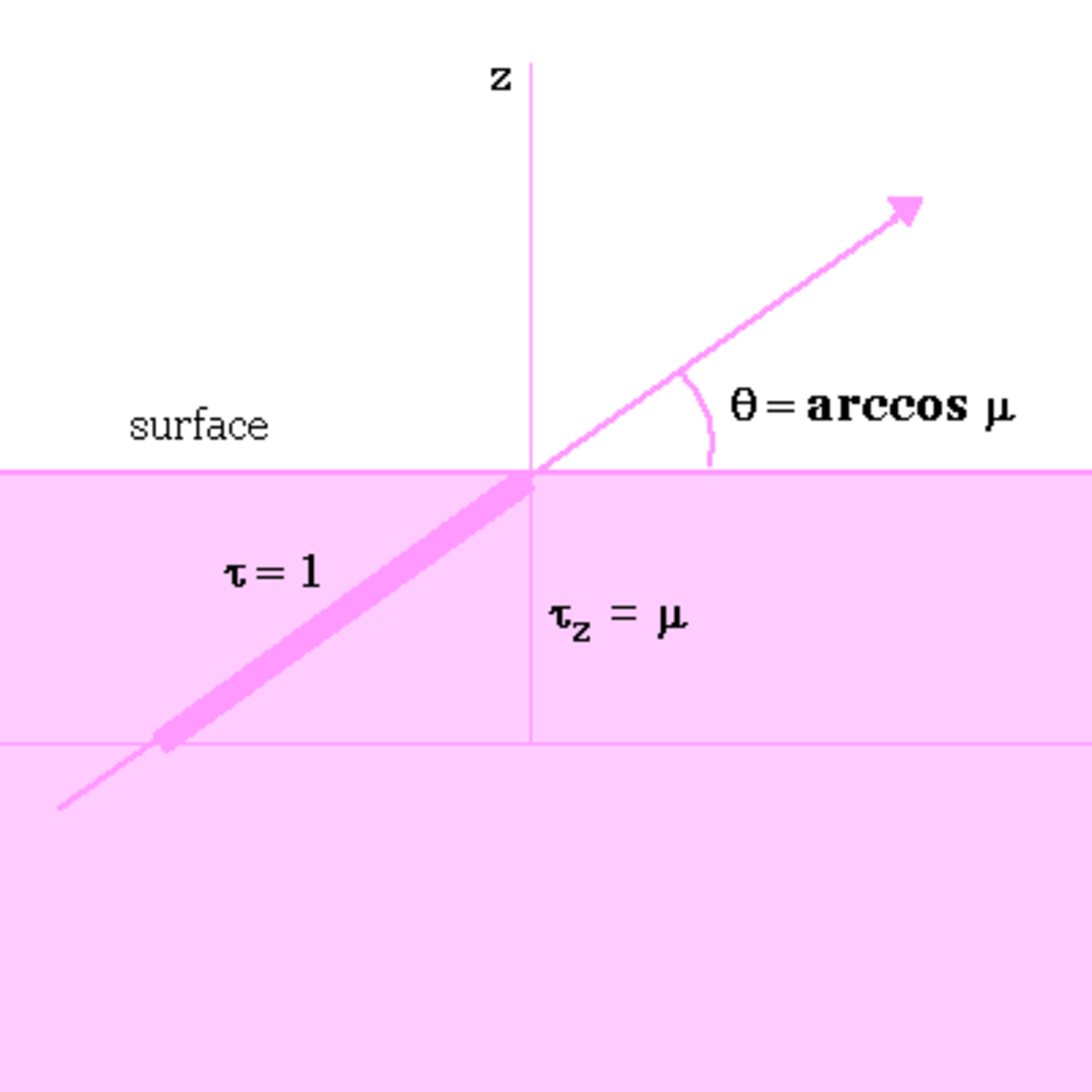
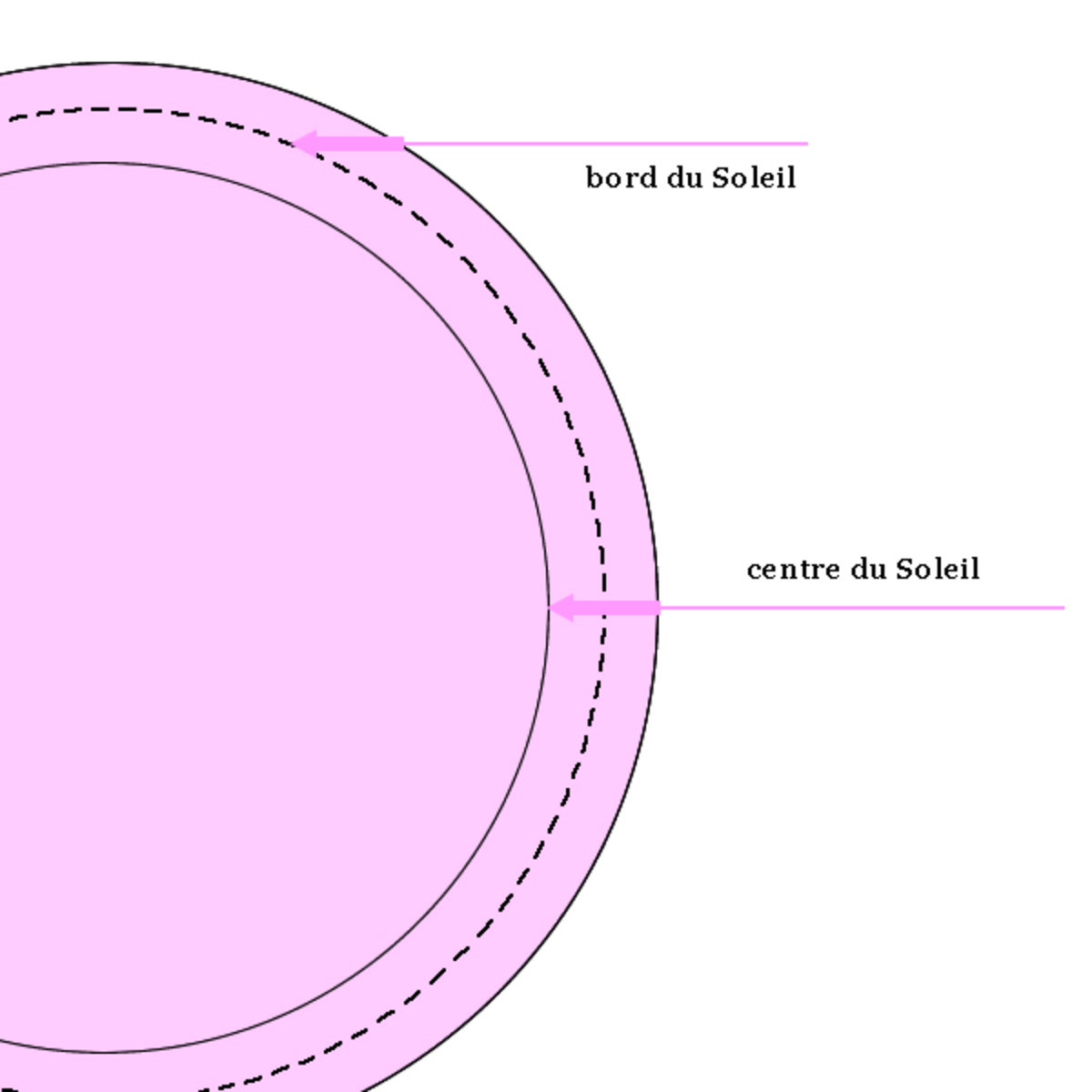
Si on se place en un point de la surface, il est facile de réaliser (figure ci-contre) que puisque l'on « voit » à τ = 1 on sonde dans la direction radiale des couches plus profondes que dans les directions tangentielles, cela à cause du facteur μ = cosθ reliant profondeur radiale et profondeur le long de la ligne de visée. Plus précisément dans la direction θ = arccosμ on « voit » la profondeur
Au bord d'une étoile, comme par exemple le Soleil, on voit donc des couches plus superficielles qu'au centre. Si la température décroît vers l'extérieur, ce qui est la situation la plus générale (et en tout cas ce que prévoient tous les modèles ETL), le bord apparaîtra plus sombre que le centre. Ainsi s'explique le phénomène de l'assombrissement centre-bord sur le disque solaire.
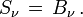
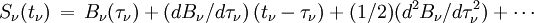
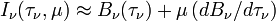
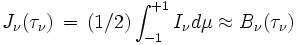
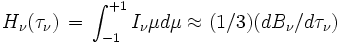
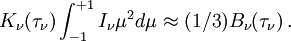
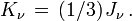
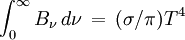
![T^{\,4} \,=\,T_0^{\,4}\, [1 + (3/2)\tau]](https://static.techno-science.net/illustration/Definitions/autres/9/99a85ef091f766b67fa4acba296083d6_19d658e95162ba9bb8a34073b90744b8.png)