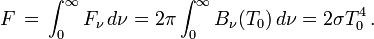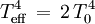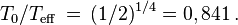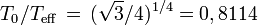Transfert de rayonnement - Définition
La liste des auteurs de cet article est disponible ici.
Géométrie sphérique
Les modèles d'étoiles les plus simples font l'hypothèse que ces objets possèdent la symétrie sphérique, c'est-à-dire qu'ils sont constitués d'un empilement de couches sphériques individuellement homogènes. Les quantités physiques, dont l'intensité du rayonnement en un point, ne dépendent alors spatialement parlant que de la variable r, distance du point au centre de l'étoile. Dans ce modèle l'intensité est une fonction du point choisi et de l'angle θ compris entre 0 et π donnant la direction du faisceau lumineux par rapport au rayon. Formellement :
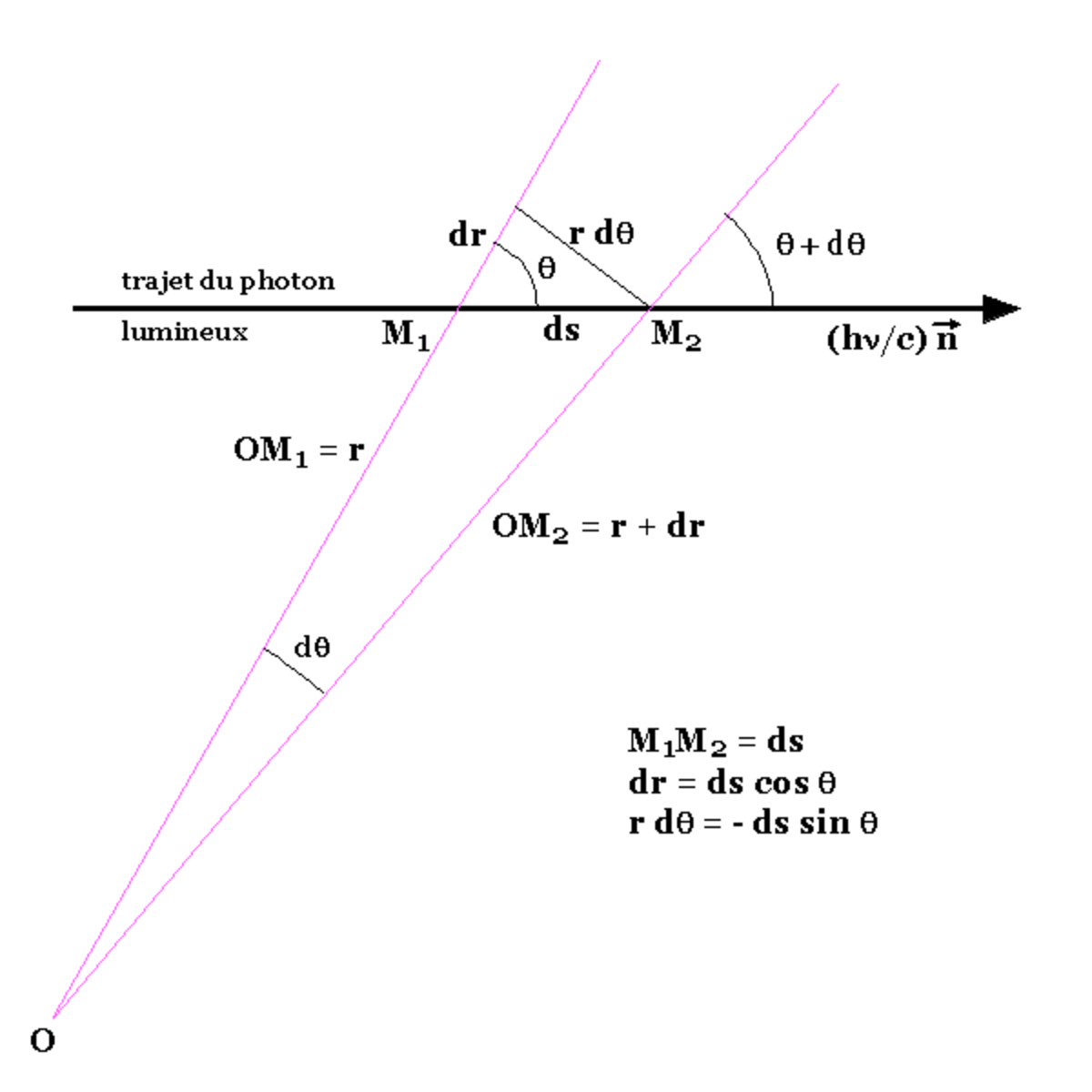
Le schéma ci-contre indique la géométrie utilisée et permet d'écrire l'équation de transfert.
La dérivée de l'intensité le long du trajet du photon est :
Comme on le voit sur la figure on a les relations
de sorte que l'équation de transfert devient
Intégrons cette équation sur l'angle solide
Le deuxième terme de gauche de l'équation conduit à une intégrale qui peut s'intégrer par parties comme :
où H est le flux défini plus haut.
Le membre de gauche de l'équation de transfert intégré sur tout l'angle solide donne donc
L'équation de transfert complète intégrée sur tout l'angle solide s'écrit donc
où J est l'intensité moyenne du rayonnement.
Si l'équilibre radiatif est réalisé cela signifie par définition qu'en intégrant sur toutes les fréquences l'énergie absorbée est égale à l'énergie émise. On a donc
En considérant alors le membre de gauche on obtient le résultat
dans lequel C est une constante, indiquant que le flux par unité de surface varie comme l'inverse du carré du rayon de la couche traversée. Physiquement cela signifie que le flux total (4π r2 H ) franchissant les couches de l'étoile reste constant, ce qui est normal si ces dernières ne contiennent aucune source d'énergie.
Température effective d'une étoile
En résumé, la température effective d'une étoile est la quantité T telle que l'énergie totale par unité de temps émise par l'astre s'exprime sous la forme
où R est le rayon de l'étoile supposée sphérique. Autrement dit, par définition
La quantité E se mesure en erg/s dans le système CGS ou en watt en unités SI.
Comme application numérique calculons la température effective du Soleil. Cet astre émet une luminosité totale
et son rayon est
Avec σ = 5,67×10-8 W⋅m-2⋅K -4 on trouve
La température effective d'une étoile est un paramètre servant à mesurer la quantité totale d'énergie lumineuse émise par cet astre. On la définit comme la température du corps noir qui émettrait dans l'espace la même quantité d'énergie. Comme une étoile ne rayonne pas comme un corps noir, cette quantité n'est pas une « vraie » température. Elle a néanmoins un certain rapport avec la température des couches superficielles de l'étoile.
Considérons un corps noir de température T. Un tel corps noir émet une intensité de lumière I indépendante de la direction égale à la fonction de Planck, soit :
D'après la définition de l'intensité I le flux à la fréquence ν émergeant d'une ouverture de surface unité faite dans la cavité du corps noir est
Le flux total émis est donc
où σ est la constante de Stefan-Boltzmann. En sens inverse, à flux donné, la température donnée par cette relation sera par définition la température effective de l'étoile. Pour obtenir le flux total émis par toute l'étoile, on intègrera encore cette quantité sur toute sa surface.
Calculons maintenant directement le flux en intégrant l'équation de transfert. Dans le cadre de l'approximation d'Eddington, la fonction source du rayonnement est donnée en fonction de la profondeur optique par la fonction linéaire
L'intensité émergente à la fréquence ν dans la direction arccosμ est égale à
Le flux traversant une surface unité est
Si on fait de plus l'hypothèse de l'ETL, la fonction source S(ν) à la surface est égale à la fonction de Planck B(T) à la température T de surface (qui maintenant, dans le cadre de l'hypothèse de l'équilibre thermodynamique local, est une « vraie » température), de sorte que l'on obtient en intégrant sur les fréquences
En comparant les deux expressions du flux à travers une surface unité, on voit que
et par conséquent
Par comparaison la résolution exacte du cas gris donne
ce qui montre que l'approximation d'Eddington est assez exacte (au moins dans certaines circonstances). On voit que le paramètre de température effective est assez voisin de la température du gaz de surface et possède de ce fait une certaine signification physique (surtout si on se contente d'ordres de grandeur) mais cela n'implique pas que le rayonnement émergent lui-même suive la loi de Planck.
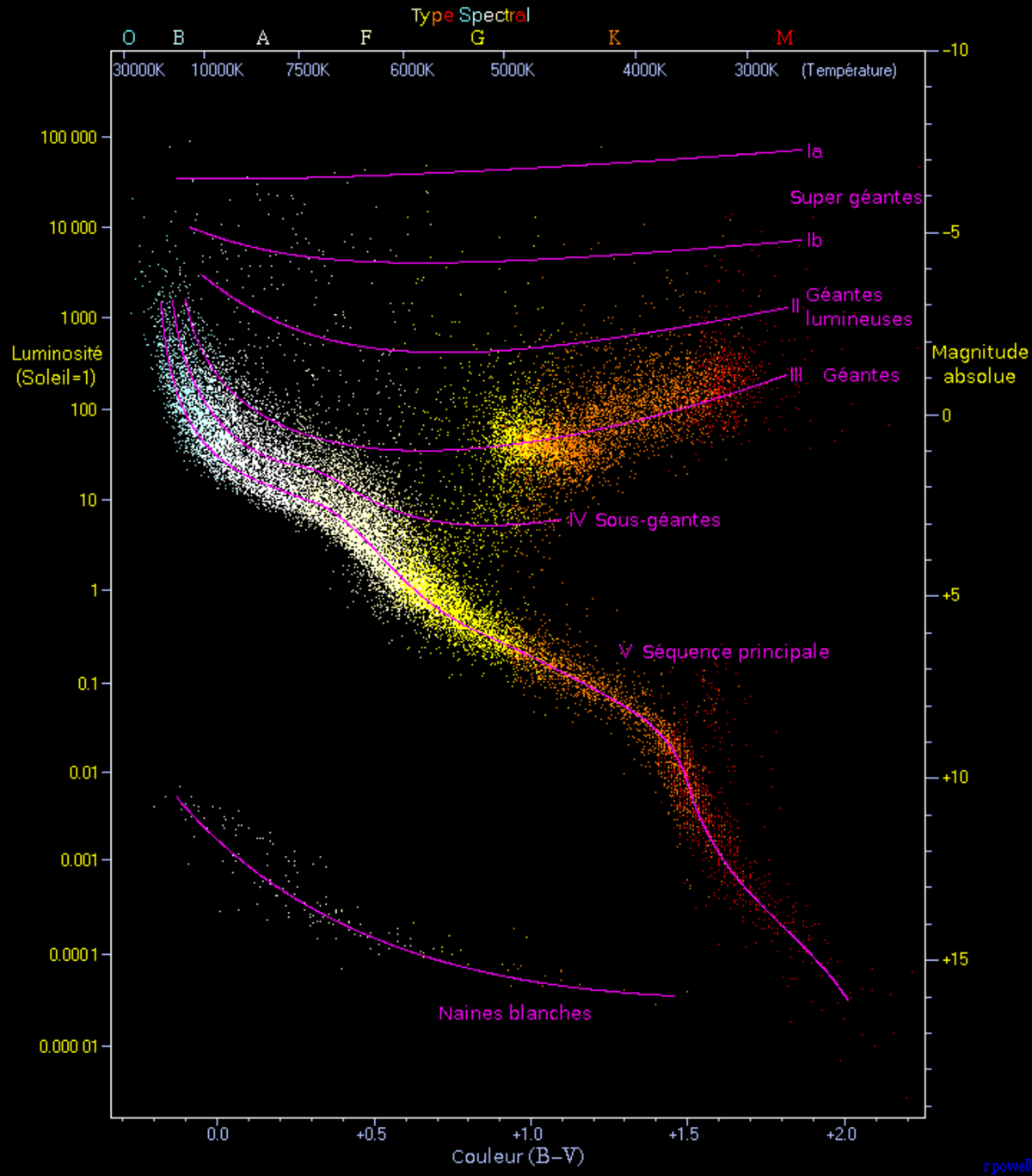
Pour reconnaître une étoile dans le ciel et en déduire ses paramètres physiques, les astronomes utilisent sa température effective et sa luminosité totale. Lorsque l'on porte les étoiles dans un diagramme basé sur ces deux paramètres (le justement célèbre diagramme de Hertzsprung-Russell, ou « diagramme HR »), les points ne se répartissent pas au hasard mais selon des séquences définies (comme la séquence principale). L'analyse de la structure de ce diagramme a permis d'établir la théorie de l'évolution d'une étoile. Les points ayant même abscisse dans ce diagramme ont même température effective et par conséquent, par définition de cette température effective, même énergie lumineuse émise par unité de surface. Il en résulte que l'ordonnée du point représentatif d'une étoile sur une même verticale est une simple mesure du carré du rayon de l'astre. Les étoiles les plus grosses (géantes ou supergéantes) sont situées dans le haut du diagramme et les plus petites (naines), dans la partie basse.
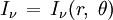
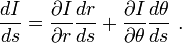
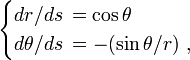
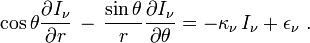
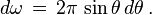
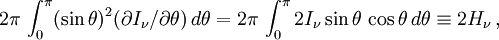
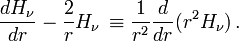
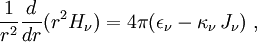
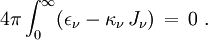
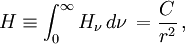
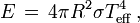
![T_{\rm eff}\,=\,[E/(4\pi R^2\sigma)]^{1/4}\,.](https://static.techno-science.net/illustration/Definitions/autres/0/0debbd8bb77f9b2c508b1814e0a8fa8e_a3d63819232a37ec8d7f82d63a9296ac.png)
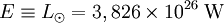
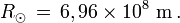
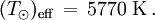
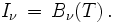
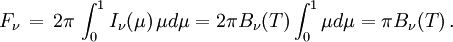
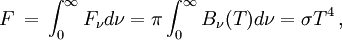
![S(\nu, \,\tau_\nu)\,=\,S_0(\nu)\,[1+(3/2)\tau_\nu]\,.](https://static.techno-science.net/illustration/Definitions/autres/5/5ab011d5979747646b68498cd17168c5_e8cf6b118ff8ef15c5e1c2ddc9db8008.png)
![I_\nu (\mu) \,=\,\int_0^\infty S(\nu, t) e^{-t/\mu}\,dt/\mu = \int_0^\infty S_0(\nu)[1+(3/2)t]\, e^{-t/\mu}\,dt/\mu= S_0(\nu)[1 + (3/2)\mu]\,.](https://static.techno-science.net/illustration/Definitions/autres/9/9b586d36cb70e6991cf12bb8d4c9be26_792c13595e585e8a35749e7e6ce7e626.png)
![F_\nu \,=\, 2\pi\int_0^\infty S_0(\nu) [1 + (3/2)\mu] \,\mu d\mu = 2 \pi S_0 (\nu)\,.](https://static.techno-science.net/illustration/Definitions/autres/4/4623c6a59712dd265095e3e4ff7fb8a3_ae110cf959647dc7d7ee376c98f97b8f.png)