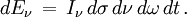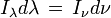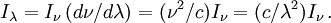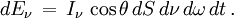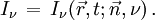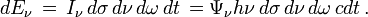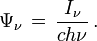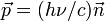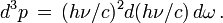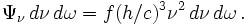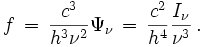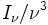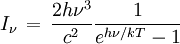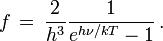Transfert de rayonnement - Définition

Introduction

Le transfert de rayonnement est le domaine de la physique décrivant l'interaction du rayonnement électromagnétique et de la matière. Cette discipline permet notamment d'analyser la propagation de la lumière à travers un milieu gazeux et joue de ce fait un rôle fondamental dans les diagnostics effectués en astrophysique à partir des spectres stellaires.

Problématique

Dans de nombreuses circonstances il est nécessaire de déterminer les propriétés intrinsèques d'un objet à partir du rayonnement observé. C'est le cas en astrophysique puisque les objets célestes sont bien trop lointains pour offrir la possibilité d'aller mesurer leurs propriétés physiques in situ. De ce fait il est nécessaire de modéliser :

• l'émission de rayonnement en tout point de l'objet en fonction des propriétés locales comme par exemple la température et la densité,
• la manière dont le rayonnement est transmis par la matière située entre le point d'émission et l'observateur terrestre.

Cette étude constitue le transfert du rayonnement.

Comme exemple simple d'action de la matière sur la lumière, le soleil est de couleur rouge au coucher et au lever non pas parce qu'il change intrinsèquement de couleur mais parce que traversant une couche plus importante d'air diffusant préférentiellement le bleu et le violet ses rayons lumineux laissent au contraire passer plus facilement l'orange et le rouge.

De façon plus générale la lumière des astres est reçue sous forme de spectres donnant la répartition de la lumière en fonction de la longueur d'onde. Le transfert de rayonnement a pour objet de calculer le spectre théorique émis par un modèle numérique d'étoile en fonction de ses caractéristiques physiques, comme sa température, sa taille, sa masse, etc. En sens inverse, c'est en comparant les spectres observés aux spectres théoriques que l'on pourra déterminer les propriétés physiques d'une étoile. Comme en astrophysique toute l'information est contenue dans les spectres la justesse du diagnostic physique dépend de façon cruciale de la qualité de la théorie du transfert utilisée.

Intensité de rayonnement

Définition de l'intensité de rayonnement

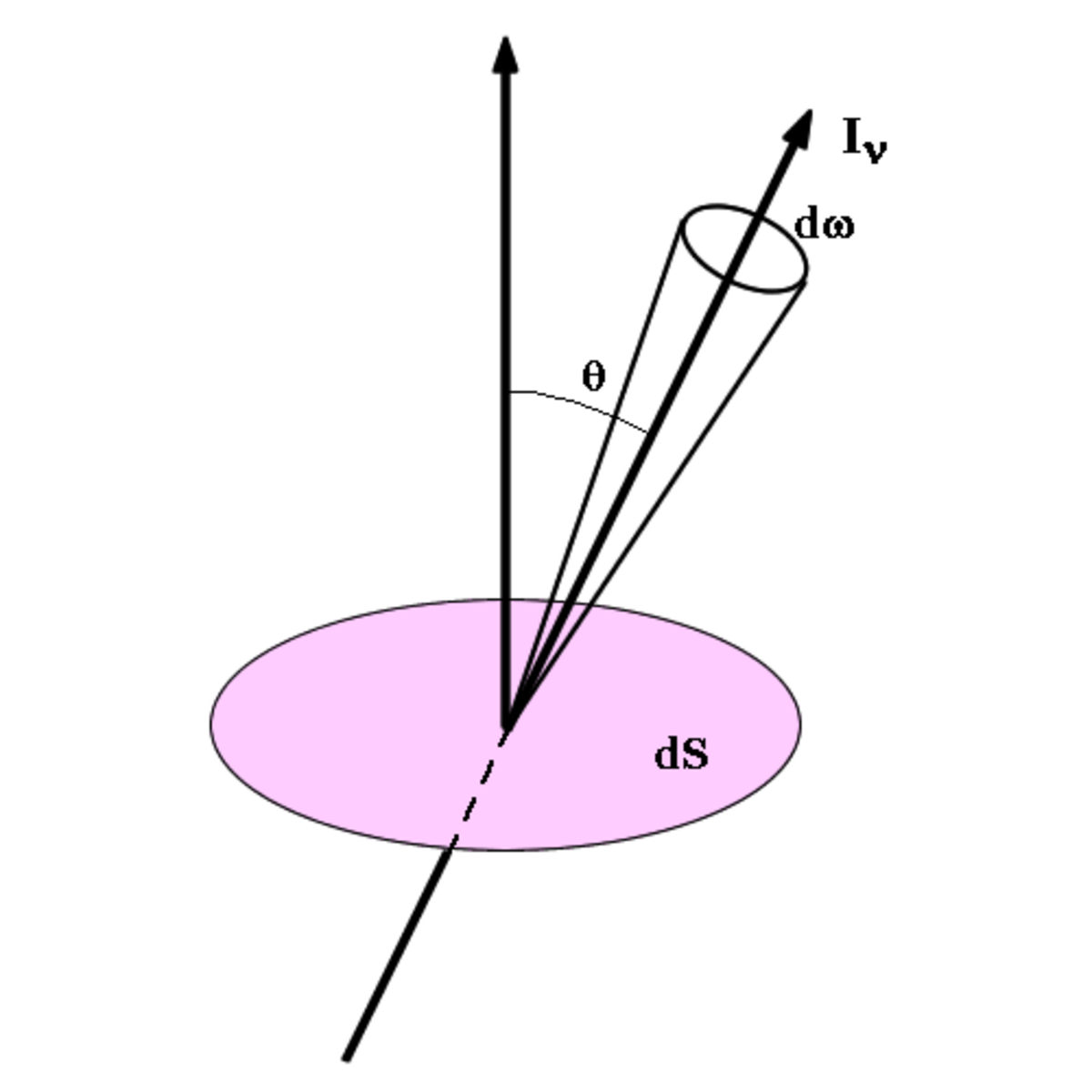
En astrophysique on caractérise le rayonnement par son intensité I (ou intensité spécifique) définie de la façon suivante. En un point donné de l'espace on considère un rayonnement contenu dans un angle solide dω, dans un intervalle de fréquence de ν à ν + dν et traversant une aire élémentaire dσ perpendiculaire à sa direction de propagation. Pour abréger la rédaction par la suite nous appellerons « photons (ou rayonnement) de classe A » les photons que nous venons de définir ainsi (c'est-à-dire traversant une surface dσ pendant le temps dt et contenus dans l'angle solide dω et dans l'intervalle de fréquence dν). La quantité d'énergie dE des photons de classe A est proportionnelle à dσ dν dω dt, ce que l'on peut écrire :

La quantité I ainsi introduite est l'intensité du rayonnement : c'est donc l'énergie par unité d'aire, par unité de temps, par unité de fréquence, par unité d'angle solide, traversant une surface perpendiculaire au faisceau de rayonnement. La quantité (I dν) s'exprime en erg⋅s^-1⋅cm^-2⋅sr^-1 dans le système CGS (utilisé de coutume en astrophysique), ou en W⋅m^-2⋅sr^-1 dans le système SI.

Attention : si on se réfère à la longueur d'onde et non pas à la fréquence, la quantité I  n'est pas égale à I  et n'a pas les mêmes dimensions physiques. On a en fait

et, puisque ν = c / λ,

Il résulte de ces formules que I  se mesure en erg⋅s^-1⋅cm^-2⋅sr^-1·Hz^-1. L'unité courante en astrophysique pour I  est le erg⋅s^-1⋅cm^-2⋅sr^-1·Å^-1 car on a l'habitude de mesurer les longueurs d'onde (du visible) en angström.

Si maintenant la surface traversée est donnée et que l'angle θ que fait la direction du rayonnement avec la normale à cette surface varie (voir la figure), la surface de l'aire perpendiculaire au rayonnement est égale à dS cosθ de sorte que la formule donnant l'énergie du rayonnement de classe A devient

Comme indiqué plus haut l'intensité du rayonnement est fonction du point considéré, de la direction, de la fréquence et éventuellement du temps. Autrement dit en réalité, de façon générale,

D'un point de vue microscopique on peut caractériser le rayonnement par la densité de photons Ψ . En tenant compte du fait que les photons de classe A possèdent l'énergie h ν et sont contenus dans un cylindre de longueur c dt, on peut réécrire l'énergie de ces photons sous la forme :

On en déduit la densité de photons

Dans une description cinétique du gaz de photons, adaptée à une analyse dans le cadre de l'espace-temps de la relativité générale, on fait plutôt intervenir la densité de photons f par unité de volume dans l'espace des phases (appelée encore fonction de distribution des photons). Comme le moment cinétique d'un photon de fréquence ν se propageant dans la direction est

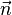
l'élément de volume dans l'espace des phases est

On peut donc écrire le nombre de photons par unité de volume dans l'intervalle dν et dans l'angle solide dω sous la forme

On en déduit que la fonction de distribution des photons s'exprime en fonction des autres grandeurs comme :

La conservation du nombre de photons le long du trajet de la lumière implique donc que la quantité

est un invariant relativiste.

Si le rayonnement est celui d'un corps noir, l'intensité lumineuse suit la loi de Planck et on a

et

On comprend sur cette expression comment s'interprète le rayonnement cosmologique diffus à 3 K. Ce rayonnement est constitué des photons qui ont été émis il y a quelque 14 milliards d'années, environ 300 000 ans après le Big Bang, sous la forme d'un corps noir de 4 500 kelvins, température égale à celle de la matière à cette époque. Depuis les photons ont évolué librement, chacun selon sa propre ligne d'univers, en conservant une répartition de Planck mais avec une diminution constante de la température inversement proportionnelle à la taille croissante de notre Univers. Pour des photons donnés, l'expression de f montre que le nombre de ces photons est conservé, et que si leur fréquence ν diminue au cours du temps, ce qui est le cas, la température T diminue aussi dans les mêmes proportions de telle sorte que le rapport hν/kT reste constant. L'Univers est environ 1 500 fois plus grand qu'à l'époque de l'émission du rayonnement de sorte que sa température est 4500/1500 = 3 (les nombres donnés sont approximatifs mais d'un ordre de grandeur parfaitement correct). Corrélativement la fréquence des photons a été divisée par 1 500 et la longueur d'onde multipliée par 1 500.