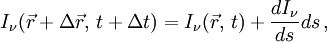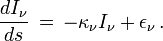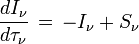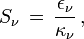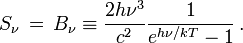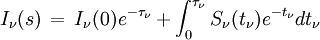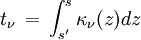Transfert de rayonnement - Définition
La liste des auteurs de cet article est disponible ici.
Généralités
Le rayonnement en un point du milieu peut
- subir une absorption, contribuant à chauffer le gaz ;
- subir une diffusion, susceptible de changer sa direction et sa fréquence ;
- être émis par les particules du gaz.
Le rayonnement subit ainsi une variation quantitative et qualitative au cours de sa propagation, ce qui se traduit par une équation différentielle contenant des dérivées par rapport aux variables de position et de temps : .
Le rayonnement dépend de
- trois variables de position,
- deux variables de direction,
- une variable de temps,
- une variable de longueur d'onde,
soit sept variables au total. Cette multiplicité de paramètres rend difficile la résolution générale du transfert du rayonnement tant d'un point de vue théorique que numérique. De plus, le rayonnement a une influence sur la matière traversée (chauffage, donc modification de la structure) qui influe rétroactivement sur le rayonnement (émission). Il s'ensuit que le problème est non linéaire et doit être résolu de manière itérative dans la plupart des cas.
Dans un grand nombre de situations l'échelle de temps radiative est très courte par rapport à l'échelle de temps thermique, de sorte que l'on peut supposer le transfert de rayonnement comme quasi-statique, éliminant ainsi la variable temporelle. Cette condition est parfois réalisée dans des expériences sur Terre mais pas toujours en astrophysique où les diverses échelles de temps et de distance peuvent devenir considérables. Cependant, par souci de simplicité, c'est surtout dans le cadre de cette hypothèse statique, à vérifier dans chaque circonstance particulière, que se fera le reste de cette présentation. Dans d'autres cas, le nombre de variables de position peut être réduit à deux ou à une seule si la géométrie du système s'y prête. Enfin, si l'on utilise parfois des valeurs bolométriques pour le rayonnement afin d'éliminer la variable de longueur d'onde, cette approximation peut s'avérer difficile à justifier lorsqu'il s'agit de construire un spectre en longueur d'onde. Toutefois l'approximation du mentionnée ci-dessous, qui consiste à ignorer la variation des propriétés d'absorption du milieu avec la longueur d'onde, permet d'obtenir des résultats intéressants.
Ajoutons enfin que la présentation faite ici ignore la polarisation de la lumière, un phénomène qui compliquerait encore les choses mais dont l'importance est pourtant grande en astrophysique car son analyse permet de faire des diagnostics sur la structure et la force du champ magnétique.
Équation de transfert
L'intensité se conserve dans le vide
Si un rayonnement se propage dans le vide sans interagir avec la matière, son intensité reste constante.
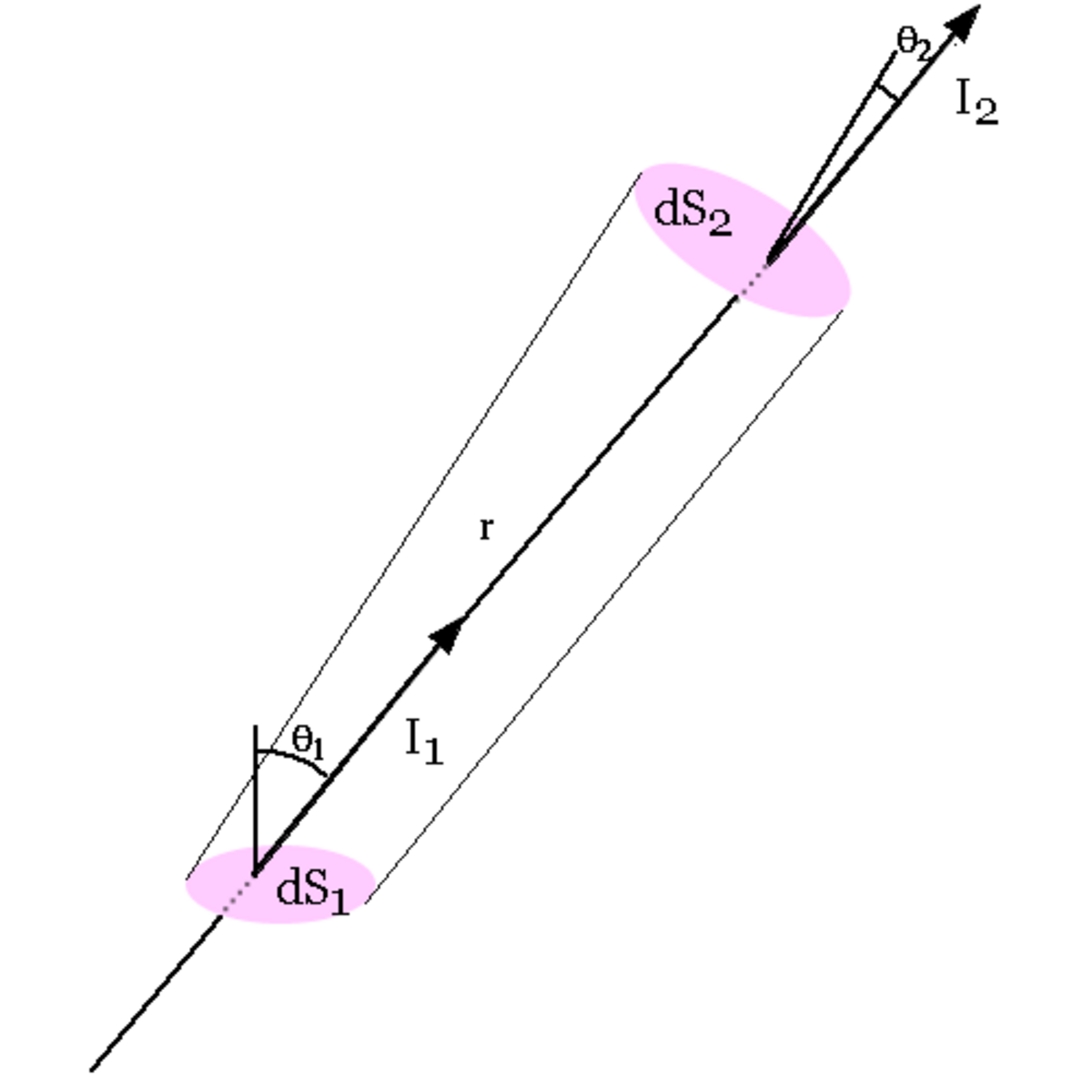
Considérons en effet un ensemble de rayons lumineux traversant à la fois deux surfaces dS et dS situées à la distance r l'une de l'autre. Soit I l'intensité du faisceau lumineux au point 1. L'énergie traversant la première surface dS par unité de temps et de fréquence est, d'après la définition précédente
Au point 2 on écrirait de même
En comparant les deux expressions, on voit que
ce qui signifie que l'intensité d'un faisceau de lumière se propageant librement est la même en tout point du parcours.
Attention toutefois ! Cela ne signifie pas qu'à surface de réception donnée l'on captera la même quantité de lumière du Soleil quelle que soit la distance à laquelle on se place. Si l'intensité du rayonnement solaire est bien la même sur la Terre et sur la lointaine planète Neptune, située 20 fois plus loin de notre étoile centrale, l'angle solide (dS/r2) sous lequel le Soleil est vu de là-bas est 400 fois plus petit que de la Terre et par conséquent une surface donnée y recevra 400 fois moins d'énergie.
Absorption du rayonnement
Quand le rayonnement traverse un milieu contenant des particules (atomes neutres ou ionisés, électrons, molécules, grains, etc.), cette matière est susceptible d'absorber ou d'émettre de l'énergie lumineuse. On caractérise la capacité d'absorption du milieu par son coefficient d'absorption κ , qui a la dimension de l'inverse d'une longueur (et se mesure donc couramment en cm-1) et est défini de telle sorte que la quantité sans dimension (κ ds) représente la fraction de rayonnement absorbée le long du trajet ds. Cette quantité définit l'épaisseur optique de la couche infinitésimale selon la formule
Si une intensité I est absorbée le long du trajet sans qu'aucune émission n'intervienne, cette intensité est atténuée selon la loi
qui s'intègre pour donner la loi d'extinction
où
et (I) est l'intensité au point choisi comme origine s = 0.
On a supposé pour écrire ces expressions que le rayonnement ne change pas avec le temps.
Remarque : si on prend la longueur d'onde au lieu de la fréquence comme variable, comme κ est relatif à une fréquence et non à un intervalle de fréquence, on aura
quantité qui a toujours la dimension de l'inverse d'une longueur (et s'exprime donc en cm-1).
L'équation de transfert du rayonnement
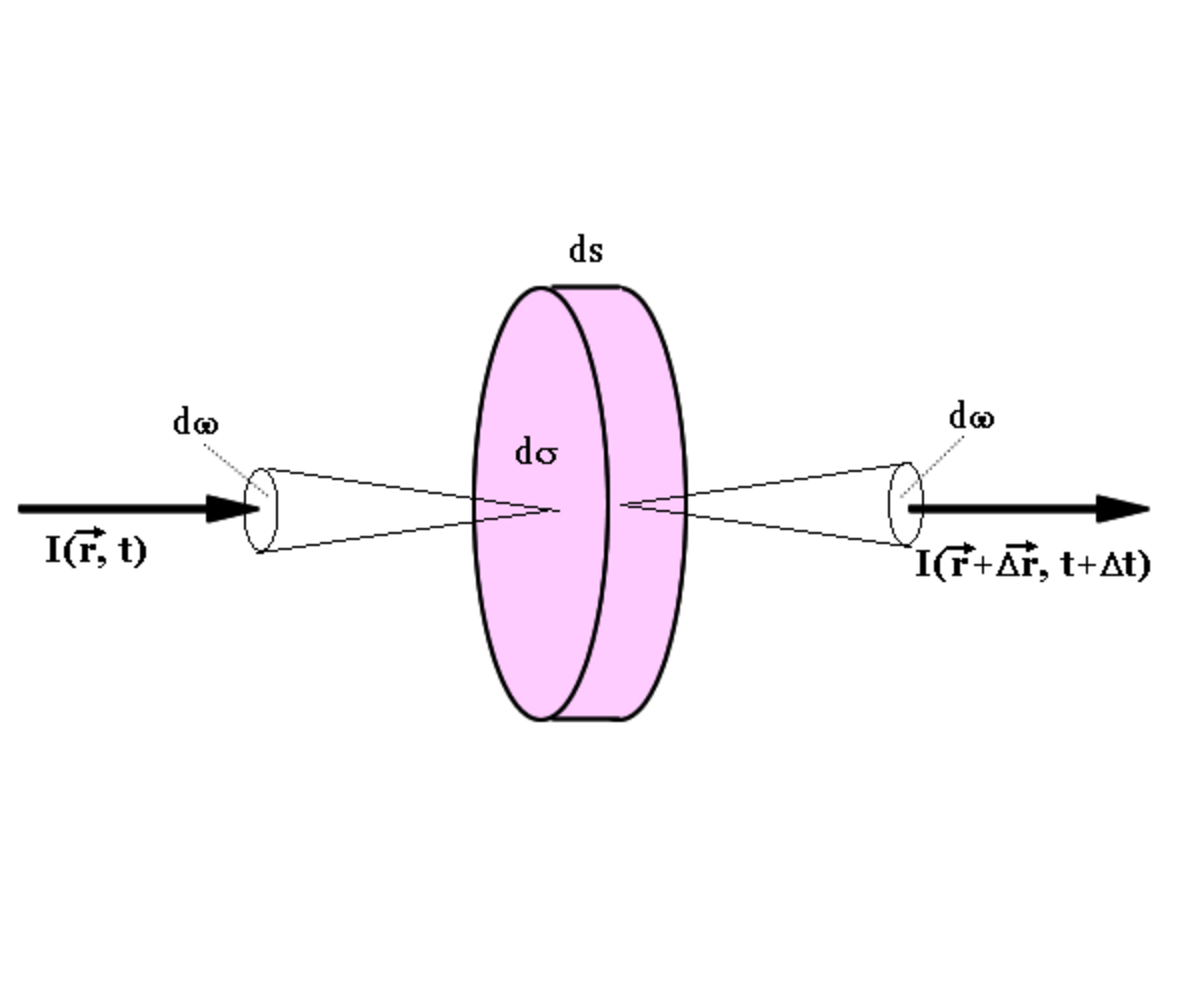
L'équation de transfert du rayonnement établit le bilan d'énergie dans le passage de photons de classe A à travers une surface dσ sur une longueur ds (voir la figure).
D'après la définition du la partie d'énergie absorbée dans le faisceau est
- partie absorbée =
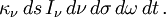
Pour calculer la partie émise par le volume traversé, on introduit un coefficient d'émission ε tel que l'énergie lumineuse de photons de classe A émise par le volume dV s'écrive sous la forme
- partie émise=
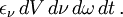
On voit que ε est une énergie par unité de fréquence par unité de volume par unité d'angle solide par unité de temps et s'exprime donc en erg·cm-3·s-1·sr-1·Hz-1.
À l'aide de ces définitions le bilan d'énergie des photons de classe A ayant traversé le volume élémentaire dσ ds s'écrit sous la forme
En se limitant au problème stationnaire, I est indépendant du temps et on a
de sorte que l'on obtient l'équation de transfert du rayonnement sous la forme :
Fonction source du rayonnement
En divisant par κ l'équation de transfert s'écrit encore
où la quantité
rapport du coefficient d'émission au coefficient d'absorption est appelée la fonction source. On voit que cette quantité a les dimensions d'une intensité et s'exprime donc dans les mêmes unités. À l'équilibre thermodynamique la fonction source est égale à la fonction de Planck
Cette équation différentielle s'intègre le long de la direction d'un faisceau lumineux sous la forme :
où
est l'épaisseur optique entre le point s' et le point s.
L'interprétation physique de cette formule est claire. Le premier terme représente l'intensité de rayonnement initial affaiblie par l'absorption sur le parcours de 0 à s. Le second représente les émissions ajoutées des différents points s’ dont la contribution est affaiblie par l'absorption entre le point d'émission s’ et le point s où l'on calcule l'intensité.
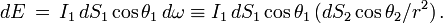
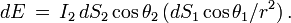
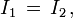
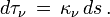
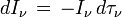
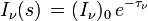
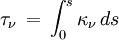
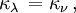
![[I_\nu(\vec{r}+\Delta\vec{r}, \,t+\Delta t) -I_\nu(\vec{r},\,t)]\,d\sigma d\omega d\nu dt = (\epsilon_\nu - \kappa_\nu I_\nu)\,d\sigma ds d\nu d\omega dt\,.](https://static.techno-science.net/illustration/Definitions/autres/5/545bec7c15804718fa3578051aa5854b_68c8f5ff595a3ede749cb902665dd588.png)