Zéro - Définition

Le zéro comme notation des bases 2, 8, 10, 16…

Dans la base dix que l’on utilise, le chiffre le plus à droite indique les unités, le deuxième chiffre indique les dizaines, le troisième les centaines, le quatrième les milliers…

Le zéro joue donc un rôle particulier dans le système arithmétique positionnel, quel qu’il soit du reste.

Rappelons que l’usage de la base 10, en provenance de l’Inde, s’est imposé en France par rapport à d’autres bases, comme par exemple 12 et 60 qui étaient utilisées dans certaines civilisations, le système vicésimal ayant laissé des traces dans la langue française, et le système duodécimal des modes de calcul chez les Britanniques.

Lorsqu’il y a des unités résiduelles, par exemple dans trente-deux (32), le chiffre des unités (2) permet de comprendre que l’autre chiffre (3) indique les dizaines.

Si l’on a un nombre entier de dizaines (par exemple trois dizaines, trente), il n’y a pas d’unité résiduelle. Il faut donc un caractère qui permette de marquer que le 3 correspond aux dizaines, et ce caractère est le 0 ; c’est ainsi que l’on comprend que « 30 » signifie « trois dizaines ».

On aurait pu utiliser n’importe quel autre caractère, par exemple un point ; ainsi, deux-cent trois se noterait « 2.3 ».

L’utilisation d’un caractère « bouche-trou » remonte à la numération babylonienne, comme indiqué ci-dessus, mais il ne s’agit pas du concept d’« absence de quantité », il s’agit juste d’une commodité de notation. Dans la numération romaine, cet artifice n’est pas utile puisque les unités (I, V), les dizaines (X, L), les centaines (C, D) et les milliers (M) sont notés avec des caractères différents. En contrepartie, la notation de nombres supérieurs à 8 999 devient problématique et les reconnaissances de structures pour le calcul mental rapide bien plus pénibles.

Propriétés arithmétiques et algébriques

En tant que nombre entier, zéro est pair.

Pour tout nombre réel (ou complexe) a :

• (0 est élément neutre pour l’addition)
• (0 est élément absorbant pour la multiplication)
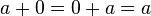
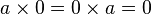
• si alors
• n’est pas défini (c’est une forme indéterminée du calcul des limites), mais il est souvent « pratique », dans certains cadres formels, de considérer que .
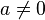
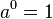
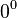
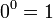
• par extension de la factorielle à l’aide de la fonction Gamma,
• 
• non défini (voir article division par zéro)
• non défini, en remarquant toutefois que le calcul lorsque les deux valeurs tendent vers zéro est la base du calcul différentiel.

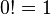
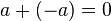
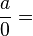
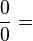
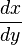
Usage étendu de zéro en mathématiques

• Zéro est l’élément neutre dans un groupe abélien muni de la loi ou l’élément neutre pour l’addition dans un anneau.
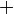
• Un zéro d’une fonction est un point dans le domaine de définition de la fonction dont l’image par la fonction est zéro ; aussi appelé racine, surtout dans le cas d’une fonction polynôme. Voir zéro (analyse complexe).
• En géométrie, la dimension d’un point est 0.
• En topologie, la dimension topologique de l’ensemble de Cantor est 0, quoiqu’il ait une dimension de Hausdorff non nulle.
• En géométrie analytique, 0 a pour nom l’origine, notée aussi O (un cas où l’ambiguïté est bénigne).
• Le concept de « presque » impossible en probabilité. Plus généralement, le concept de presque nulle part en théorie de la mesure.
• Une fonction zéro est une fonction avec 0 comme seule valeur de sortie possible. Une fonction zéro particulière est le morphisme zéro. Une fonction zéro est l’identité dans le groupe additif des fonctions.
• Zéro est l’une des trois valeurs de retour possibles de la fonction de Möbius. Si on entre un entier x² ou x²y, la fonction de Möbius retournera zéro.
• C’est un nombre de Pell.