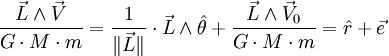Lois de Kepler, démonstration - Définition

Les lois de Kepler ont été découvertes à partir des observations de Tycho Brahé (1546 - 1601) et de leur analyse poussée par Johannes Kepler (1571 - 1630). Elles ont été démontrées par Isaac Newton (1642 - 1727) en 1687 dans les Principia, œuvre considérée comme un monument de la pensée humaine. Les démonstrations qui suivent ne sont pas celles de Newton, pour des raisons diverses (cf. Principia et Calculus).

Des explications plus abordables se trouvent sous lois de Kepler.
Le lien externe : Démonstration des trois lois de Kepler et propriétés d'une ellipse est plus complet.

Conventions et notations pour les démonstrations qui vont suivre

Pour simplifier, prenons le Soleil comme origine du référentiel, l'axe z perpendiculaire à la droite passant par le Soleil et la planète et perpendiculaire à la direction de la vitesse de la planète au temps t = 0. L'axe x dans la direction correspondante à la distance la plus petite entre le Soleil et la planète. La distance la plus grande entre le Soleil et la planète sera dans la direction -x.

la masse du Soleil.
la masse de la planète.
la position du Soleil. C'est l'origine du référentiel.
la position de la planète.
l'instant où la planète se trouve le plus proche du Soleil.
la position de la planète au temps .

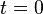
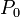
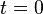
Elle s'appelle le périhélie. C'est le point de la trajectoire près de Hélios; soit le plus proche du Soleil.

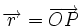
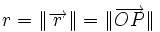
le vecteur allant du Soleil à la planète.
= la distance du Soleil à la planète.
le vecteur allant du Soleil à la planète au temps .
la vitesse de la planète.
la vitesse de la planète au temps .
la force d'attraction de la planète par le Soleil.
le moment cinétique relativement à l'origine où se trouve le Soleil.

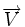
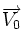
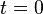
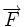
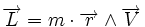
C.f. le produit vectoriel " " pour des informations sur cet opérateur.

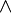
Première partie de la première loi (1609)

Dans un référentiel immobile par rapport au Soleil, la trajectoire d'une planète se trouve dans un plan.

• Démonstration :

Cela résulte du fait que le Soleil attire la planète selon une force centrale. C'est-à-dire une force qui est toujours dirigée de la planète vers le Soleil.

En effet, étant données une position et une vitesse initiales, cela définit un plan. Selon nos conventions ci-dessus, c'est le plan passant par l'origine O, contenant les axes x et y.

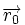
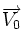
Puisque la force est centrale, elle et l'accélération sont dans une direction se trouvant dans ce même plan. Donc les variations de vitesses et les variations de positions resteront dans ce même plan. En conclusion toute la trajectoire restera dans ce plan.

La deuxième loi de Kepler donnera une deuxième démonstration de cette partie.

Deuxième loi, loi des aires (1609)

Soit A(t) l'aire de la surface balayée par le rayon vecteur durant le mouvement, alors cette seconde loi stipule que des aires égales sont balayées dans des temps égaux.

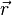
• Démonstration :

En dérivant le moment cinétique par rapport au temps, on obtient :

qui vaut 0.

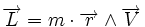
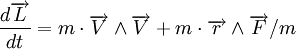
Donc le moment cinétique est un vecteur constant. Cela résulte du fait que la force est centrale (cf. force centrale, mouvement)

D'autre part :

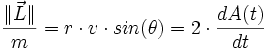
En conséquence :

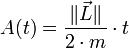
Deuxième partie de la première loi (1609)

Dans un référentiel immobile par rapport au Soleil, la trajectoire d'une planète est elliptique, un foyer étant le Soleil. Le Soleil n'est un des foyers qu'approximativement, du fait que sa masse M est très supérieure à celle de la masse m de la planète.
Pour être exact, il faudrait se placer au centre de gravité du système Soleil - planète.

• Démonstration :

Ce fait est directement lié au fait que l'hodographe est un cercle dans le cas de l'attraction universelle de Newton.

Le principe fondamental de la dynamique s'écrit :

    où    

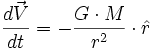
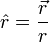
Par changement de variable, on a :

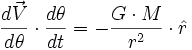
(Attention : L'angle noté θ dans ce paragraphe est différent de celui du paragraphe précédent)

Rappelons l'expression de la loi des aires obtenue au paragraphe précédent :

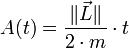
ainsi, l'aire balayée pendant un temps égale . Or cet aire vaut .

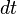
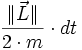
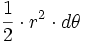
Donc

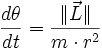
En combinant ces deux relations, on obtient :

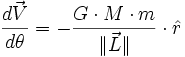
D'où en intégrant par rapport à θ :    car   

= le vecteur unité perpendiculaire à dans le plan de la trajectoire, dirigé dans le sens le plus proche de celui de la vitesse.

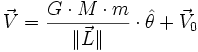
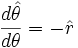
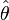
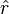
Ce résultat s'appelle : théorème de Hermann, Laplace, Runge, Lenz, Hamilton : cf. invariant de Runge Lenz.

L'hodographe est un cercle excentré par rapport à l'origine des vitesses. Il en résulte que la trajectoire est une conique : si l'origine des vitesse est à l'intérieur du cercle, la conique est une ellipse; si elle est à l'extérieur, c'une hyperbole; cas limite : une parabole. Ce théorème de cinématique est très vieux, mais on l'attribue à tort à Hamilton; il était encore enseigné dans le cours de cosmographie de " math-élem " (terminale S actuelle) : cf. par exemple Lebossé, cours de mathématiques élémentaires. On va en donner la démonstration due à Landau, très algébrique :

Le théorème précédent se réécrit après multiplication vectorielle par et simplifications :

s'appelle le vecteur d'exentricité. On montre qu'il est constant. (C.f. lien externe n°2)

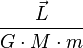
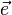
puis en effectuant le produit scalaire avec et en simplifiant :

, avec

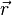
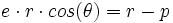
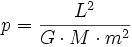
soit

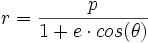
Ce qui est la définition focale d'une conique en coordonnées polaires, d'excentricité et de paramètre , d'angle polaire ayant pour origine le périhélie, comme il est usuel de le faire.

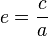
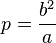
Si on prend l'aphélie comme origine :

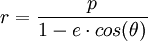
Troisième loi (1618)

Le carré de la période varie comme le cube du demi-grand axe  :

s'appelle la constante de Gauss : elle est connue avec une extraordinaire précision, dix chiffres significatifs et vaut 0.01720209895. Alors que n'a que 5 misérables chiffres significatifs.

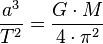
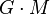
Démonstration :

• En utilisant :   et   ,
  

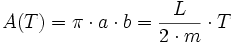
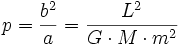
puis en supprimant de ces égalités, on obtient le résultat annoncé.

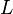
On remarquera ce fait extraordinaire, toutes les ellipses de même grand axe, quelle que soit leur excentricité , ont la même période jusqu'à la circulaire où .

La disposition des planètes est assez remarquable (loi de Titius-Bode), tant par leur faible excentricité que par leur faible inclinaison sur le plan écliptique moyen. Le scénario cosmogonique de Levinson-Morbidelli le justifie, écartant ainsi Pluton et (90377) Sedna des planètes ordinaires et les faisant entrer dans la catégorie des " petits " objets de la ceinture de Kuiper.