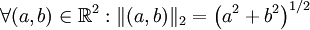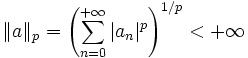Espace vectoriel normé - Définition
Un espace vectoriel normé est une des structures importantes rencontrées en analyse, et plus particulièrement en analyse fonctionnelle. Développée notamment par David Hilbert et Stefan Banach, cette notion se définit souvent sur le corps des nombres réels ou complexes, mais la définition s'étend sur tout corps muni d'une valeur absolue.
Formellement, un espace vectoriel normé sur un corps K muni d'une valeur absolue est la donnée d'un K-espace vectoriel E et d'une application
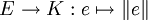
- Séparation : Pour tout e dans E, on a :
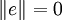
- Homogénéité : Pour tout r dans K et pour tout e dans E,
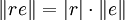
- Inégalité triangulaire : Pour tout e, f on a :
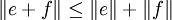
Dans le cas oû K=R ou C, la notation | r | désigne la valeur absolue ou le module.
Topologie d'un espace vectoriel normé
On peut, à partir de la norme
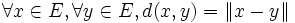
On vérifie aisément que les trois axiomes qui définissent une distance sont vérifiés. De plus, la distance est invariante par translation, et homogène, au sens où :
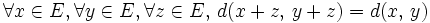
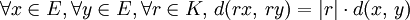
L'espace E est alors muni de la topologie associée à cette distance. C'est bien évidemment un espace topologique sur le corps topologique K.
Si K est le corps des réels ou des complexes, les boules forment une base de voisinages convexes de 0 : E est alors un espace vectoriel topologique localement convexe sur K.
Un espace vectoriel topologique localement convexe sur K est dit normalisable si sa topologie peut être définie par une norme. Il existe, y compris sur R ou sur C de nombreux exemples d'espaces vectoriels topologiques localement convexes séparés intéressants mais non normalisables, par exemple parce qu'ils ne sont pas localement convexes.
Un espace vectoriel normé réel ou complexe complet (pour la distance associé) est appelé espace de Banach.
Exemples
Espaces normés de dimension finie
Normes canoniques sur Kn
L'espace
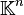
- Norme-1
- Soit
-
-
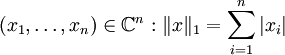
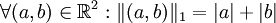
- Norme-2
- Soit
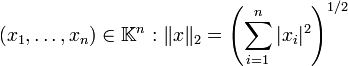
- Dans
-
- Norme-infinie
- Soit
![\ x=(x_1,\dots,x_n)\in\mathbb K^n: \|x\|_\infty = \max_{i\in[1,\dots,n]}|x_i|](https://static.techno-science.net/illustration/Definitions/autres/f/fdadfc573c6f1e8e4390822507396415_aa4722c452ac5fcfdabd4428c712f352.png)
- Norme-p
- Soit
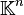
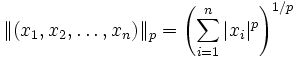
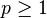
- C'est un espace vectoriel normé.
![\ x=(x_1,\dots,x_n)\in\mathbb K^n: \|x\|_\infty = \max_{i\in[1,\dots,n]}|x_i|](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/fdadfc573c6f1e8e4390822507396415_aa4722c452ac5fcfdabd4428c712f352.png)
La notation
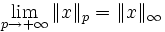
Autres espaces de dimension finie
Tout
En effet, E est isomorphe à
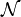
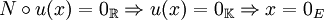
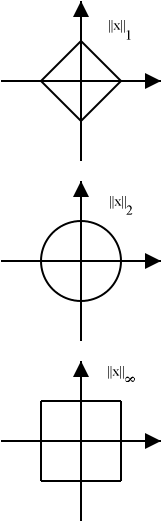
Cercles carrés
Bertrand Russell aimait à donner comme exemple d'oxymore l'expression " cercle carré ". S'il s'agit bien d'un oxymore en géométrie euclidienne, les cercles carrés existent bel et bien lorsqu'on adopte par exemple la norme infinie. L'ensemble des points de norme 1 est un carré, et c est un cercle dans la mesure où tous leurs points sont à égale distance de l'origine. Pour la norme-1, on obtient un carré incliné à 45°.
Espaces normés de dimension infinie
- L'ensemble
-
-
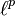
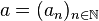
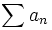
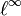
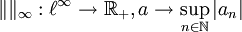
- Le
-
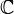
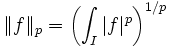
- et de la norme-infini :
-
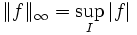
- que l'on retrouve avec:
-
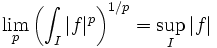
- On l'appelle également norme de la convergence uniforme.
Propriétés des espaces normés de dimension finie
Soit E un espace vectoriel de dimension finie sur
- Il n'existe qu'une seule topologie sur E qui en fasse un espace vectoriel topologique séparé, et cette topologie est normalisable ;
- Pour cette topologie, E est homéomorphe à
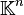
- En particulier, toutes les normes sur E sont équivalentes ;
- E est complet ;
- Les parties compactes de E sont les fermés bornés ;
- La boule unité (fermée) de E est compacte ;
- Toute application linéaire de E dans un espace vectoriel normé quelconque est continue.
Théorème de Riesz
Si la boule unité (fermée) d'un espace vectoriel réel ou complexe normé E est compacte, alors E est de dimension finie.
