Espace topologique - Définition
En mathématiques, les espaces topologiques permettent de définir dans un contexte très général des concepts comme la convergence, la continuité et la connexité. Ces concepts apparaissent dans presque toutes les branches des mathématiques, ils sont donc centraux dans la vision moderne des mathématiques. La branche des mathématiques qui étudie ces espaces s'appelle la topologie.
La notion d'espace topologique est une définition axiomatique, formalisée par une structure ensembliste. Les axiomes sont minimaux, et en ce sens c'est la structure la plus générale pour étudier les concepts cités.
Cet article est technique, une vision générale et historique est donnée dans Topologie.
Concepts
Définitions
- Un espace topologique est un couple
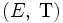

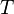

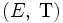
- L'ensemble vide et

- Toute réunion d'ouverts est un ouvert,
- i.e. si
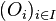
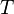
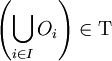
- i.e. si
- Toute intersection de deux ouverts est un ouvert,
- i.e. si
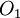
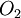
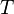
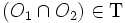
- i.e. si
- L'ensemble
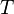

Il résulte de la théorie élémentaire des ensembles que toute intersection finie d'ouverts est un ouvert.
- Les fermés d'une topologie sont les complémentaires des ouverts. Par conséquent, la famille des fermés contient

Il résulte de la théorie élémentaire des ensembles que toute intersection de fermés est un fermé, et que toute réunion finie de fermés est un fermé.
- Il est d'usage de rappeler la présence de la partie vide à l'axiome 1 ; c'est toutefois en bonne rigueur superflu, puisqu'on peut l'obtenir en appliquant l'axiome 2 à la réunion indexée par l'ensemble vide.
- Un des premiers rôles de la topologie est de décrire les voisinages des points. C'est une notion-clé pour comprendre la topologie. Elle sert par exemple à la définition de continuité ou de limite en un point. Cette notion est formalisée dans l'article voisinage. Rappelons ici simplement qu'une partie de

Exemples
- Un exemple simple est
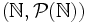

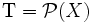
En contrepartie de la simplicité, elle n'offre pas beaucoup d'intérêt.
- Autre exemple sans intérêt : la topologie grossière sur


- Un exemple plus intéressant sur les entiers est
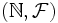
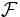
- L'article sur les voisinages démontre qu'il existe une topologie associée à tout espace métrique. Un ouvert


- L'ensemble des nombres réels est donc muni naturellement d'une topologie issue de sa distance. Un ouvert est alors une union d'intervalles ouverts.
- La topologie induite d'un sous-ensemble




- D'autres exemples de topologies plus sophistiquées sont donnés dans l'article voisinage.
- Le cube de Hilbert
![[0,1]^\N](https://static.techno-science.net/illustration/Definitions/autres/8/87018ac4548501371d4f40dc5e7d0c8f_15f275f7db35fb316a0d384444b8ad0b.png)
- L'ensemble de Cantor est source de nombreux exemples et contre-exemples.
Applications continues
Définitions
Un des premiers intérêts de la notion d'espace topologique est de pouvoir définir une application continue. Il existe deux approches, l'approche locale donnée dans l'article voisinage et qui définit la continuité en un point, et l'approche globale qui définit la continuité en tout point.
- Définition globale. Une application
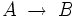
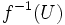
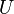
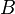
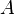
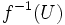
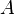
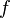
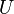
- Définition locale. Soit
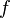

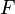

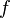
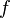

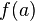

- Équivalence de la continuité locale en tout point et de la continuité globale. Si une application est globalement continue l'image réciproque d'un ouvert contenant
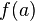

Une application bijective continue et dont la réciproque est continue est appelée un homéomorphisme.
La notion d'application continue est développée en détail dans l'article continuité.
Exemples
- L'application identité d'un espace topologique dans lui-même est continue. En effet l'image réciproque de tout ouvert est lui-même donc est ouvert.
- Une application constante d'un espace topologique dans un autre est continue. En effet l'image réciproque est soit l'ensemble vide soit l'ensemble de départ tout entier.
- l'application
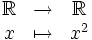
Limite
Adhérence
Cette notion est développée dans un article spécifique Adhérence. Nous ne développerons cette notion que dans la mesure où elle est nécessaire pour formaliser la notion de limite.
En topologie l'adhérence d'une partie X d'un espace topologique est le plus petit ensemble fermé qui contient cette partie. On la note souvent
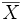
Une autre façon de définir les espaces topologiques consiste à faire appel à la notion prétopologique d'adhérence : on définit une adhérence sur un ensemble E comme une application qui à toute partie A de E associe une partie contenant A, l'adhérence de la partie vide restant vide. Dans le cas où l'adhérence est idempotente et où l'adhérence de l'union de deux parties est égale à l'union des adhérences, on dit que l'adhérence est topologique. Un espace topologique peut se définir comme un ensemble muni d'une adhérence topologique. Les ouverts sont alors les complémentaires des parties stables pour l'adhérence.
En termes d'adhérences, une application d'un espace topologique dans un autre est continue si et seulement si l'image d'un point adhérent à une partie est nécessairement adhérente à l'image de cette partie.
Définition
La notion de limite, si elle existe, décrit le comportement qu’une fonction devrait avoir si elle était définie en ce point. L’exemple le plus simple est le cas d’une fonction définie sur un intervalle ouvert de

Soit
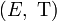
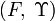
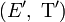

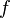
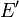
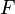

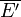
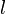
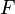
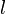
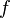

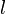
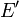

- Remarque 1
- La notion de limite est développée dans l’article Limite.
- Remarque 2
- Si le point

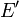
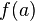
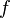

Propriétés
- On dit qu’un espace topologique est séparé ou de Hausdorff ou T2 lorsque deux points distincts quelconques admettent des voisinages disjoints.
- On dit qu’un espace vérifie la propriété de Borel-Lebesgue lorsqu’on peut extraire un sous-recouvrement fini de tout recouvrement ouvert. On parle aussi d’espace quasi-compact.
- Un espace quasi-compact et séparé est dit compact.
Exemples
- Le premier exemple historique d’espace topologique est l’ensemble des nombres réels. Cet exemple est celui qui est à la base de la théorie des espaces topologiques. Il apparaît comme un cas particulier de la deuxième famille d’exemples donnés ici.
- Les espaces métriques et, en particulier, les espaces vectoriels normés sont des espaces topologiques.
- Il existe de nombreuses classes d'espaces topologiques (espaces vectoriels topologiques, espace de Banach, de Fréchet, de Hilbert, de Hausdorff, de Kolmogorov, de Montel, de Baire, compacts, quasi-compacts, précompacts, paracompacts, bien enchaînés, complets, connexes, simplement connexes, connexes par arcs, localement compacts, localement connexes, groupe topologique, anneau topologique etc.).

















































