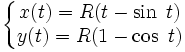Cycloïde - Définition
La cycloïde droite, aussi appelée roue d'Aristote ou roulette de Pascal, est une courbe plane transcendante, trajectoire d'un point fixé à un cercle qui roule sans glisser sur une droite. Il s'agit donc d'une courbe cycloïdale particulière dont la directrice est une droite et dont le point directeur est situé sur le cercle lui-même; c'est un cas particulier de roulette.
Par exemple, la valve (point directeur) d'une roue de vélo avançant en ligne droite décrit une épicycloïde et non pas une cycloïde car elle n'entre pas en contact avec la chaussée (directrice). Par contre, le chewing-gum (point directeur) collé sur le pneu décrira une cycloïde car il rentre en contact avec la chaussée (directrice) à chaque tour de roue.
Étymologie et histoire
Le mot vient du grec kuklos (cercle, roue) et eidos (forme, semblable à), bien que cette courbe n'ait pas été connue des Grecs et ne fut baptisée qu'en 1599 par Galilée.
Elle fut étudiée pour la première fois au XVe siècle par Nicolas de Cues alors qu'il essayait de déterminer la surface du cercle par intégration. En 1626, Mersenne en reprit l'étude et essaya, sans succès, de déterminer l'aire sous une arche de cycloïde. Il faudra attendre 1634 pour que son confrère Roberval démontre que cette aire est égale à trois fois l'aire du cercle qui l'a générée. Descartes, qui fut consulté sur ce calcul, le trouva intéressant mais trivial. Galilée, pour sa part, avait étudié ce problème pendant quarante ans mais n'était arrivé au même ratio que par une méthode empirique mettant en jeu des mesures de poids ; il crut d'ailleurs que ce ratio n'était pas entier.
La cycloïde et le calcul de ses propriétés furent alors l'objet de défis constants entre mathématiciens, si bien qu'elle fut surnommée " l'Hélène des géomètres ". Après Descartes, Pascal (sous le pseudonyme de Dettonville) offrit un prix à qui résoudrait deux problèmes liés à la cycloïde et au mouvement du pendule. En 1658, Christopher Wren démontra que la longueur d'une arche de cycloïde est égale à quatre fois le diamètre du cercle qui l'a générée. En 1673, Christiaan Huygens l'évoqua dans un traité sur le pendule synchrone. A cette époque, un technicien eut l'idée de suspendre le pendule à deux lames correctement recourbées (" joues ") pour obtenir l'isochronisme du battement, préalable indispensable pour permettre la construction d'horloges marines et donc la détermination du " secret des longitudes". Huygens démontra que la forme de ces lames correspondait à des morceaux de cycloïdes[1]. Enfin, ses propriétés brachistochrones furent étudiées à partir de 1696 par Jean Bernoulli, puis par Isaac Newton, Leibniz, Jacques Bernoulli et L'Hôpital. Il s'agissait d'un des premiers problèmes de variations, et son étude fut le point de départ de l'élaboration du calcul des variations.
Définition mathématique
La courbe peut être définie paramétriquement par l'équation suivante :
On peut également la définir par une équation intrinsèque :
-
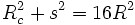
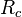

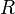
Propriétés et applications
Propriété générales
Une arche de cycloïde a une longueur de 8 R et une aire de 3π R².
La roulette de la pointe d'une cardioïde roulant sur une cycloïde de même longueur est rectiligne.
La radiale de la cycloïde est un cercle de rayon 2 R.
La développée et la développante de la cycloïde sont des cycloïdes translatées.
La brachistochronie
C'est une courbe brachistochrone au sens de Roberval, c'est-à-dire qu'une cycloïde représente la courbe sur laquelle doit glisser sans frottement et sans vitesse initiale, un point matériel pesant placé dans un champ de pesanteur uniforme de sorte que son temps de parcours soit minimal parmi toutes les courbes joignant deux points fixés. Autrement dit, c'est la courbe de descente la plus rapide pour aller d'un point A à un point B.
La tautochronie
La demi-arche de cycloïde est également une courbe tautochrone, c'est-à-dire une courbe telle que tout point matériel lâché sans vitesse initiale sur la courbe arrive en un point donné ( celui ayant la plus basse altitude pour la cycloïde ) en un temps indépendant du point de départ.
L'isochoronie
Elle est enfin une courbe isochrone au sens de Huygens, c'est-à-dire telle qu'un point matériel se déplaçant sans frottement sur elle a un mouvement périodique dont la période est indépendante de la position initiale.
Ces deux dernières propriétés expliquent son utilisation dans la conception de pendules cycloïdaux en horlogerie.
Autres propriétés remarquables
La trajectoire d'une particule soumise sans vitesse initiale à un champ électrique et un champ magnétique orthogonaux uniformes est une cycloïde orthogonale au champ magnétique.
Des propriétés caustiques particulières font que la cycloïde est également utilisée en optique.