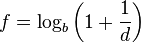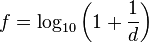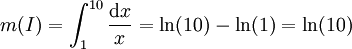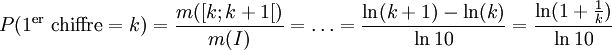Loi de Benford - Définition
La loi de Benford, ou loi des nombres anormaux car elle est surprenante lorsqu'on la découvre, montre que dans la vie de tous les jours, le chiffre 1 est plus fréquent que le 2, lui-même plus fréquent que le 3, etc.
De façon générale, la loi donne la valeur théorique f de la fréquence d'apparition de la première décimale d d'un résultat de mesure exprimé dans une base b donnée au moyen d'une unité.
Système décimal
En particulier, pour le système décimal (base 10), on a donc :
Ce qui aboutit au tableau de résultats suivants :
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| f | 30,1 | 17,6 | 12,5 | 9,7 | 7,9 | 6,7 | 5,8 | 5,1 | 4,6 |
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| f | 30,1 | 47,7 | 60,2 | 69,9 | 77,8 | 84,5 | 90,3 | 95,4 | 100 |
Il existe également une discrète sur-présentation des premiers chiffres en ce qui concerne le second chiffre significatif. Cette sur-présentation tend à s'annuler au delà.
Les exemples illustrant cette loi sont nombreux : prenez la suite des 100 premiers carrés, la fréquence des nombres commençant par 1 est nettement supérieure aux fréquences des carrés commençant par 2, 3,4 etc etc. En constituant la liste de 100 nombres, produits de deux ou trois nombres tirés au hasard (dans un grand intervalle), de nouveau la fréquence des nombres commençant par 1 est nettement plus élevée que les autres fréquences.
Les suites numériques qui convergent exactement comme le stipule la loi de Benford sont, en fait, assez rares : parmi celles ci, on peut citer la suite de Fibonacci, la suite des n !... Dans la vie réelle, la décroissance des probabilités suivant le premier chiffre est largement constatée mais la convergence vers les valeurs de la loi de Benford n'est qu'approximative.
Au contraire, cette loi n'est pas vérifiée si la série de données comporte des contraintes quant à l'échelle des valeurs vraisemblables : la taille des individus ne suit, à l'évidence, pas la loi de Benford puisque la quasi totalité des mesures commence par le chiffre " 1 ".
Explication
La forme précise de la loi de Benford peut être expliquée si l'on admet que les logarithmes des nombres sont uniformément distribués. Cela signifie qu'un nombre a autant de chances d'être entre 100 et 1000 (logarithme entre 2 et 3) qu'il a de chances de se trouver entre 10 000 et 100 000 (logarithme entre 4 et 5). Pour de nombreux ensembles de nombres, et tout particulièrement ceux qui croissent exponentiellement, comme les chiffres d'affaire d'entreprises et les cours de bourse, cette supposition est raisonnable.
Ébauche de démonstration de la loi de Benford
Choisissons un nombre réel stictement positif appartenant à un intervalle I.
On cherche la probabilité de son premier chiffre non nul, indépendemment de toute autre caractéristique.
Cela correspond à la recherche d'une mesure m sur l'ensemble I, supposé mesurable, avec :
-
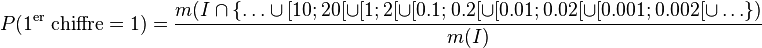
-
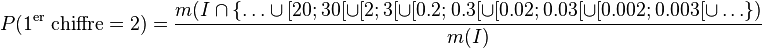
-
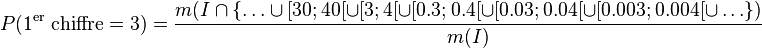
- etc.
On suppose que I est construit comme une union de produits de l'intervalle [1;10[ par des réels ai > 0 ; c'est-à-dire : I = ∪ ai × [1;10[ pour des ai > 0. Donc, on travaille dans le groupe multiplicatif des réels strictement positifs (car c'est ainsi que la topologie de ce groupe est construite).
L'ensemble des réels strictement positifs muni de la multiplication étant un groupe topologique séparable et localement compact, il existe une et une seule mesure (à un coefficient multiplicateur près) qui soit invariante par la loi de groupe : la mesure de Haar du groupe.
Cette mesure est
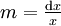
Prenons I = [1;10[, on a :
Et on a :
Comme la mesure m est invariante par le produit, en prenant I = ∪ ai × [1;10[ avec ai = 10n , on arrive au même résultat (on peut aussi le vérifier par le calcul).
Ébauche faite à partir d'un travail exposé sur le site de l'Université Paris 5[1]. Il manque dans ces deux exposés un argument convaincant sur la nécessité d'utiliser la mesure de Haar.
Historique
Cette distribution aurait été découverte une première fois en 1881 par Simon Newcomb, un astronome américain, après qu'il se fut aperçu de l'usure (et donc de l'utilisation) préférentielle des premières pages des tables de logarithmes (alors compilées dans des ouvrages). Frank Benford, aux alentours de 1938 arriva aux même résultats après avoir répertorié des dizaines de milliers de données (longueurs de fleuves, cours de la bourse, etc.) et a donné son nom à la loi.
Application
La loi de Benford est utilisée aux États-Unis, ainsi que dans d'autres pays, dont la France, pour détecter des fraudes fiscales, suite aux idées exposées en 1972 par Hal Varian.