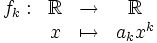Cet article fait partie de la série Mathématiques élémentaires

Algèbre

Analyse

Arithmétique

Géométrie

Logique (La logique (du grec logikê, dérivé de logos (λόγος), terme inventé par Xénocrate signifiant...)

Probabilité (La probabilité (du latin probabilitas) est une évaluation du caractère probable d'un évènement. En mathématiques, l'étude des probabilités est un sujet de grande importance donnant lieu à de...)

Statistique (Une statistique est, au premier abord, un nombre calculé à propos d'un échantillon. D'une façon générale, c'est le...)

En mathématiques élémentaires (Les mathématiques élémentaires regroupent les mathématiques abordées et abordables dans l'enseignement primaire et secondaire. Une page méta est dédiée à ce...), une fonction polynôme (En algèbre, une fonction polynôme, ou fonction polynomiale est définie comme étant une application associée à un polynôme à coefficients dans un anneau (souvent un corps) commutatif K de la forme :) est une somme de fonctions de la forme

La fonction f_k est appelée fonction monôme (À la fin XIXe siècle, le monôme était une manifestation étudiante sous la forme d'un cortège ou d'une procession en file indienne. Il est généralement effectué la...) de degré (Le mot degré a plusieurs significations, il est notamment employé dans les domaines suivants :) k. On dit donc qu'une fonction polynôme (En mathématiques, un polynôme est la combinaison linéaire des puissances d'une variable, habituellement notée X. Ces objets sont largement utilisés en pratique, ne serait-ce que parce qu'ils donnent localement une valeur approchée de toute...) est une somme de fonctions monômes.

En général, les fonctions polynômes étudiées en mathématiques (Les mathématiques constituent un domaine de connaissances abstraites construites à l'aide de raisonnements logiques sur des concepts tels que les nombres, les figures, les structures et les transformations. Les...) élémentaires sont définies sur à coefficients dans . Mais on peut parfois trouver des fonctions polynômes définies sur à coefficients dans . Ces fonctions polynômes sont des cas particuliers de fonctions polynômes plus générales dans lesquelles la variable (En mathématiques et en logique, une variable est représentée par un symbole. Elle est utilisée pour marquer un rôle dans une formule, un prédicat ou un algorithme. En statistiques, une variable peut...) et les coefficients peuvent appartenir à d'autres ensembles que ou .

Par abus de langage, on appelle parfois une fonction polynôme un polynôme, confondant ainsi une fonction avec un polynôme formel. Cette confusion est sans gravité (La gravitation est une des quatre interactions fondamentales de la physique.) dans le cadre des mathématiques élémentaires mais peut conduire à des contresens en algèbre générale (L'algèbre abstraite, ou algèbre générale, ou encore algèbre universelle est la branche des mathématiques qui porte principalement sur l'étude des structures...).

Exemples

Un exemple de polynôme de degré 5

Pour éviter une surcharge de notation, on ne précisera que l'expression de la fonction polynôme, étant entendu que son ensemble (En théorie des ensembles, un ensemble désigne intuitivement une collection d’objets (les éléments de l'ensemble), « une multitude qui peut être...) de départ est toujours ou .

Si , f est une fonction polynôme de degré 5.

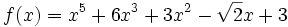
Le degré d'une fonction polynôme non nulle est le degré de sa fonction monôme de plus haut degré. Une fonction constante non nulle est une fonction monôme de degré 0. La fonction constante nulle est appelée fonction polynôme de degré égal à

Une fonction affine (En mathématiques élémentaires, une fonction affine est une fonction de la variable réelle dont la représentation graphique est une droite. C'est une fonction polynôme de degré inférieur ou égal à un....), définie par f(x) = ax + b et telle que a soit non nul, est une fonction binôme ( en mathématique, binôme, une expression algébrique ; voir aussi binôme de Newton et coefficient binomial un binôme est un groupe de deux personnes, voir Équipe en binôme en...) du premier degré. Une fonction définie par f(x) = ax² + bx + c et telle que a soit non nul, est une fonction trinôme du second degré.

Racine

Si f(r) = 0, on dit que r est une racine du polynôme f et on démontre que l'on peut factoriser le polynôme par (x - r).

Binôme de degré un

f(x) = ax + b avec a non nul

racine r = -b/a

factorisation : f(x) = a(x - r)

Trinôme du second degré

• article principal: équation (En mathématiques, une équation est une égalité qui lie différentes quantités, généralement pour poser le problème de leur identité. Résoudre l'équation consiste à déterminer...) du second degré

Selon le signe du discriminant (En mathématiques, le discriminant est une notion algébrique. Il est utilisé pour résoudre des équations du second degré. Il se généralise pour des polynômes de degré quelconque...), une fonction polynôme du second degré possède 0 ou deux racines (éventuellement confondues) dans mais elle possède toujours deux racines dans . Quand elle possède deux racines, elle se factorise en

f(x) = a(x - r_{1)(x - r2)}

Cas général

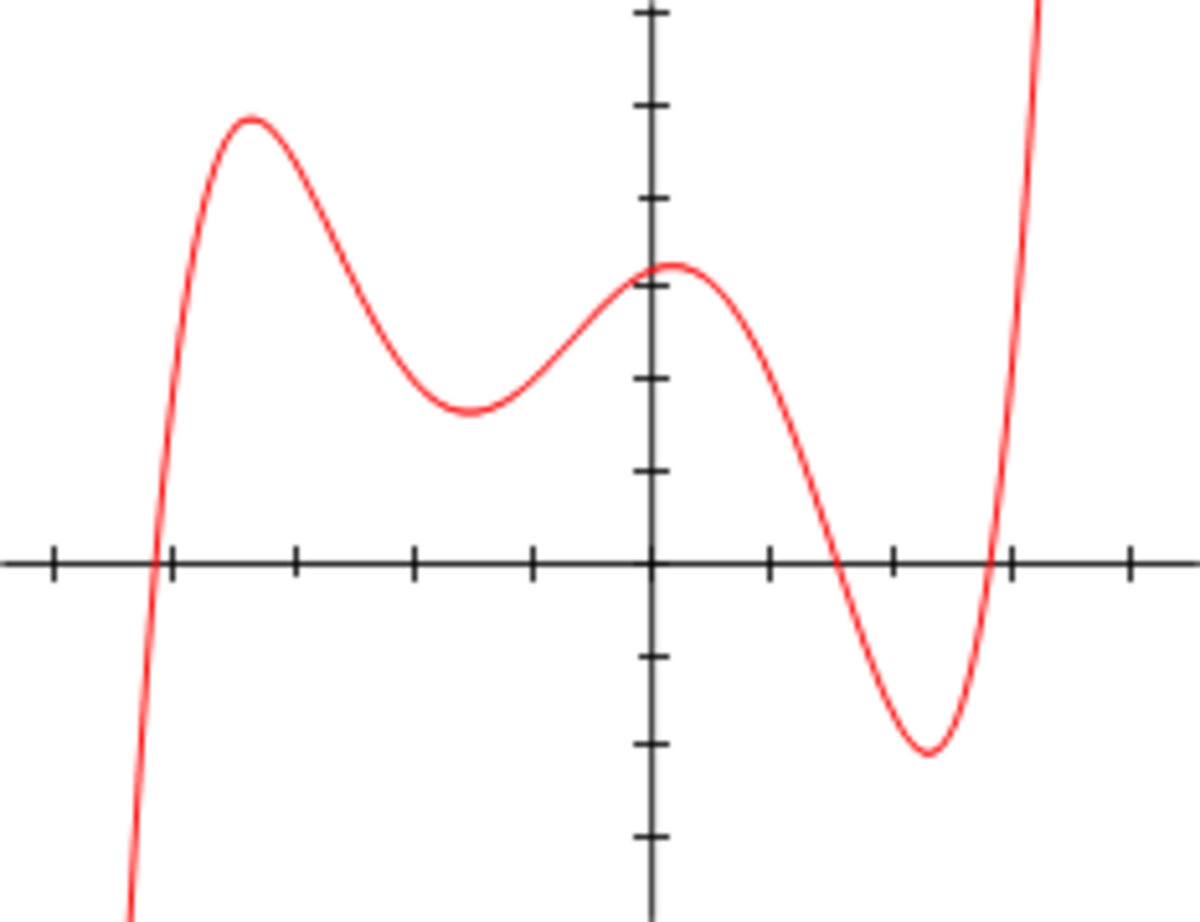
En mathématiques élémentaires, la recherche (La recherche scientifique désigne en premier lieu l’ensemble des actions entreprises en vue de produire et de développer les connaissances scientifiques. Par extension métonymique, la recherche...) de racine d'un polynôme de degré supérieur à 2 ne se fait qu'expérimentalement en cherchant des racines " évidentes ".

Si f(x) = x³ + 3x² - 16x + 12, on remarque que 2 est racine de f en calculant f(2), entre autres images de valeurs simples. La factorisation se fait alors en utilisant des méthodes diverses comme la méthode de Horner (La méthode de Horner est utilisée dans le calcul polynomial, soit pour calculer la valeur d'une fonction polynomiale en un point, soit pour calculer le quotient d'un polynôme par X - a.), la division (La division est une loi de composition qui à deux nombres associe le produit du premier par l'inverse du second. Si un nombre est non nul, la fonction "division par ce nombre" est la réciproque de la fonction...) de polynômes ou l'identification (voir plus bas).

Identification

On démontre qu'une fonction polynôme définie sur ou de degré n ne peut pas s'annuler plus de n fois. On peut donc dire que deux fonctions polynômes de degrés inférieurs ou égaux à n et coïncidant sur plus de n points sont nécessairement identiques (même degré et mêmes coefficients). C'est ce qu'on appelle l'identification.

C'est une propriété efficace qui permet de trouver des formes plus appropriées pour certaines expressions.

Exemple 1 : trouver a et b tels que x³ + 3x² - 16x + 12 = (x - 2)(x² + ax + b) pour tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou l'univers.) x réel.

On pose f(x) = x³ + 3x² - 16x + 12

On pose g(x) = (x - 2)(x² + ax + b)

On développe g(x) : g(x) = x³ + (a - 2)x² + (b - 2a)x - 2b

Puisque les deux polynômes coincident sur plus de 3 points, ils sont identiques, de même degré (degré trois) et de même coefficient (En mathématiques un coefficient est un facteur multiplicatif qui dépend d'un certain objet, comme une variable (par exemple, les coefficients d'un...). Autrement dit f(x) = g(x) pour tout x ssi

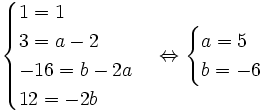
On obtient alors f(x) = (x - 2)(x² + 5x - 6)

Exemple 2 : L'étude de la fonction polynôme f définie par f(x) = x⁴ - 4x³ + 9x² - 10x -1 révèle l'existence d'un axe de symétrie d'équation x = 1 pour la courbe (En géométrie, le mot courbe, ou ligne courbe désigne certains sous-ensembles du plan, de l'espace usuels. Par exemple, les droites, les segments, les lignes polygonales et les cercles sont des courbes.) représentative et pousse (Pousse est le nom donné à une course automobile illégale à la Réunion.) à chercher deux réels a et b tels que, pour tout réels x, f(x) = (x-1)⁴ + a(x - 1)² + b.

On pose g(x) = (x-1)⁴ + a(x - 1)² + b

On développe g(x) grâce aux identités remarquables :

g(x) = x⁴ - 4x³ + (6 + a)x² - (4 + 2a)x + 1 + a + b

On identifie

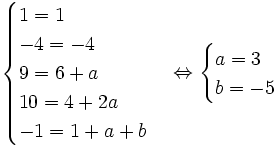
On obtient alors f(x) = (x-1)⁴ + 3(x-1)² - 5

Exemple 3: On cherche à mettre la fonction rationnelle (En mathématiques, une fonction rationnelle est un rapport de fonctions polynômes à valeurs dans un corps K. En pratique, ce corps est généralement (corps des réels) ou (corps des...) définie pour tout x différent de 2 par sous forme réduite. Bref, on cherche à trouver trois réels a, b et c tels que, pour tout x différent de 2,

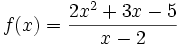
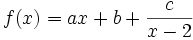
On pose

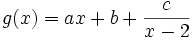
On réduit au même dénominateur

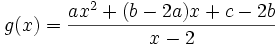
Les deux fonctions ayant même dénominateur, elle coïncident pour tout x différent de 2 si et seulement si les numérateurs coïncident sur ce même ensemble. Les numérateurs sont des polynômes du second degré qui coïncident sur plus de 2 points, on peut donc identifier leurs coefficients

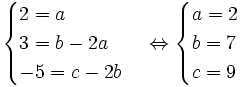
On obtient alors

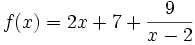
Éléments de symétrie

La courbe représentative d'une fonction polynôme f a pour axe de symétrie l'axe (Oy) si et seulement si tous les monômes constituant f sont de degré pair. C'est probablement cette propriété qui est à l'origine de la dénomination de fonction paire pour toute fonction dont la courbe représentative a pour axe de symétrie l'axe (Oy).

De même, la courbe d'une fonction polynôme f a pour centre de symétrie le point (Graphie) O si et seulement si tous les monômes constituant f sont de degré impair.

Étude

L'étude de la fonction affine (En mathématiques, affine peut correspondre à :) et de la fonction du second degré est faite de manière exhaustive. Quelques résultats sont à connaître sur une fonction polynôme degré supérieur.

Une fonction polynôme est dérivable sur . Pour k non nul, la dérivée (La dérivée d'une fonction est le moyen de déterminer combien cette fonction varie quand la quantité dont elle dépend, son argument, change. Plus précisément, une dérivée est une expression (numérique ou...) de la fonction monôme f_k définie par est . La dérivée d'une fonction monôme constante est la fonction nulle.

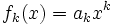
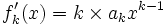
Une fonction polynôme est donc continue sur .

La limite à l'infini (Le mot « infini » (-e, -s ; du latin finitus, « limité »), est un adjectif servant à qualifier quelque chose qui n'a pas de limite en nombre ou en taille.) d'une fonction polynôme est égale à la limite de son monôme de plus haut degré.

• La limite en de a_nxⁿ est si a_n est positif et sinon.
• La limite en de a_nxⁿ est
  • si a_n est positif et n pair
  • si a_n est positif et n impair
  • si a_n est négatif et n pair
  • si a_n est négatif et n impair.

Quelques ouvertures intéressantes

Ne font pas partie des mathématiques élémentaires des résultats intéressants comme la recherche des racines de polynômes de degré trois par la méthode de Cardan, ni les racines de polynôme de degré quatre. L'existence de telles méthodes pourrait laisser croire qu'il existe des méthodes générales pour des degrés supérieurs ou égaux à cinq, mais il n'en est rien.

L'existence de racines pour un polynôme de degré deux est la première prise de contact avec le théorème (Un théorème est une proposition qui peut être mathématiquement démontrée, c'est-à-dire une assertion qui peut être établie comme vraie au travers d'un raisonnement logique construit à partir...) fondamental de l'algèbre (L'algèbre, mot d'origine arabe al-jabr (الجبر), est la branche des mathématiques qui étudie, d'une façon...) qui stipule (En botanique, les stipules sont des pièces foliaires, au nombre de deux, en forme de feuilles réduites située de part et d'autre du pétiole, à sa base, au point d'insertion sur la tige.) que tout polynôme de degré n à coefficients dans possède n racines, éventuellement confondues, dans .